RLS con ggplot2

La librería ggplot2 con la función geom_smooth() muestra gráficamente el ajuste de la Regresión Lineal Simple.

Código en R:

datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))

   Fecha PrecioInterno PrecioInternacional Producción Exportaciones     TRM
1 ene-00        371375              130.12        658           517 1923.57
2 feb-00        354297              124.72        740           642 1950.64
3 mar-00        360016              119.51        592           404 1956.25
4 abr-00        347538              112.67       1055           731 1986.77
5 may-00        353750              110.31       1114           615 2055.69
6 jun-00        341688              100.30       1092           869 2120.17
     EUR
1 1916.0
2 1878.5
3 1875.0
4 1832.0
5 1971.5
6 2053.5

X = datos$Producción
y = datos$Exportaciones

regression <- lm(Exportaciones ~ Producción, data = datos)
regression

Call:
lm(formula = Exportaciones ~ Producción, data = datos)

Coefficients:
(Intercept)   Producción
   235.3538       0.6769

library(ggplot2)

En la función geom_smooth() se agrega el argumento method = "lm" para el ajuste de Regresión Lineal (Linear Method).

ggplot(data = datos, aes(X, y)) +
    geom_point() +
    geom_smooth(formula = y ~ x, method = "lm") +            # RLS
    labs(title = paste("R2 = ", signif(summary(regression)$r.squared, 2),  # R 2 con dos decimales
                         "Intercept =", signif(regression$coef[[1]], 2),   # Beta 0 con dos decimales
                         " Slope =", signif(regression$coef[[2]], 2),      # Beta 1 con dos decimales
                         " Valor - p =", signif(summary(regression)$coef[2,4], 2)))   # Valor p con dos decimales

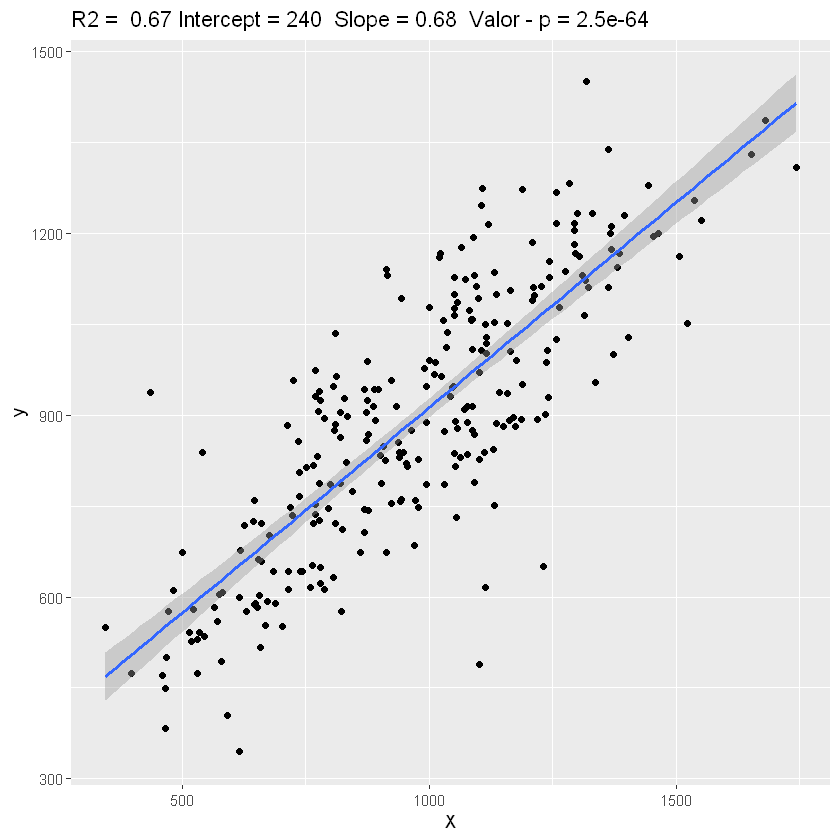
En geom_smooth() muestra por defecto el \(SE(\hat{\beta_1})\): Es el error estándar de \(\hat{\beta_1}\), con el argumento se.

ggplot(data = datos, aes(X, y)) +
    geom_point() +
    geom_smooth(formula = y ~ x, method = "lm", se = F) +       # Se elimina el error estándar de Beta 1
    labs(title = paste("R2 = ", signif(summary(regression)$r.squared, 2),
                         "Intercept =", signif(regression$coef[[1]], 2),
                         " Slope =", signif(regression$coef[[2]], 2),
                         " Valor - p =", signif(summary(regression)$coef[2,4], 2)))

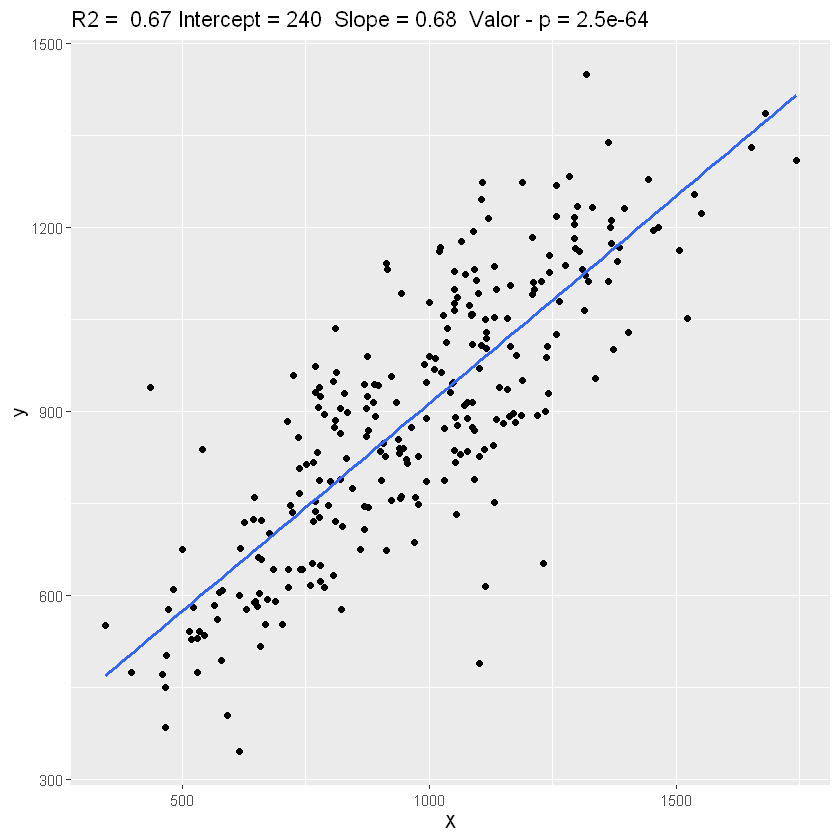
y_pred = regression$fitted.values
print(head(y_pred))

       1        2        3        4        5        6
680.7329 736.2360 636.0596 949.4494 989.3846 974.4935

residuales = regression$residuals
print(head(residuales))

         1          2          3          4          5          6
-163.73288  -94.23604 -232.05960 -218.44941 -374.38461 -105.49352

Gráficos del modelo de RLS con ggplot2:

p1 <- ggplot(data = datos, aes(X, y)) +
        geom_point() +
        geom_smooth(formula = y ~ x, method = "lm", se = F) +
        theme_bw() +
        labs(title = paste("Beta 0 =", signif(regression$coef[[1]], 2),
                           "Beta 1 =", signif(regression$coef[[2]], 2),
                           "\nR2 =", signif(summary(regression)$r.squared, 2),
                           "\nValor-p =", signif(summary(regression)$coef[2,4], 2)),
            x = "Producción de café",
            y = "Exportaciones de café")

p2 <- ggplot(data = datos, aes(X)) +
        geom_histogram(color = "#63B8FF", fill = "#63B8FF", bins = 30) +
        labs(title = "Distribución Residuales",
            x = "Residuales",
            y = "Frecuencia relativa") +
        theme_bw()

p3 <- ggplot(data = data.frame(residuales),
             aes(sample = residuales)) +
        stat_qq() +
        stat_qq_line() +
        labs(title = "QQ-Plot") +
        theme_bw()

p4 <- ggplot(data = data.frame(y_pred, residuales),
                aes(x = y_pred, y = residuales)) +
        geom_point(color = "#63B8FF") +
        geom_hline(yintercept = 0, color = "darkred") +
        labs(x = "Predicciones", y = "Residuales") +
        theme_bw()

Los cuatro gráficos de los resultados de la regresión se mostrarán en uno solo. Se usará la función grid.arrange() de la librería library(gridExtra).

library(gridExtra)
grid.arrange(p1, p2, p3, p4, ncol = 2)

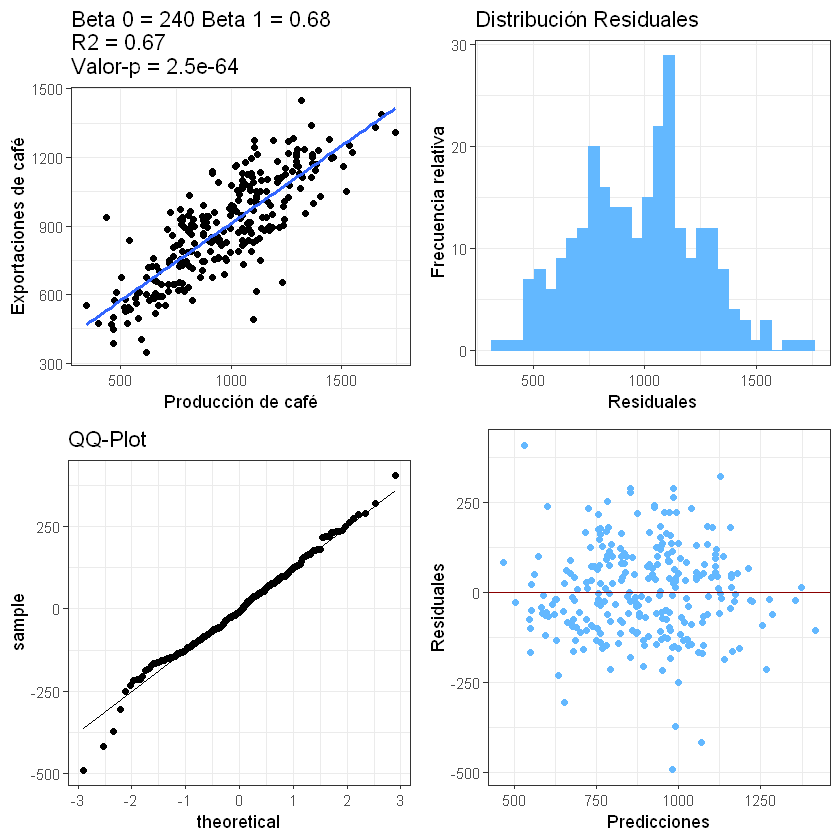
Para darle más importancia a un gráfico el entorno visual se dividirá por vectores y los números dentro de cada vector serán los gráficos.

library(gridExtra)
grid.arrange(p1, p2, p3, p4, ncol = 4,
             layout_matrix = cbind(c(1,1,1), c(1,1,1), c(2,3,4), c(2,3,4)))

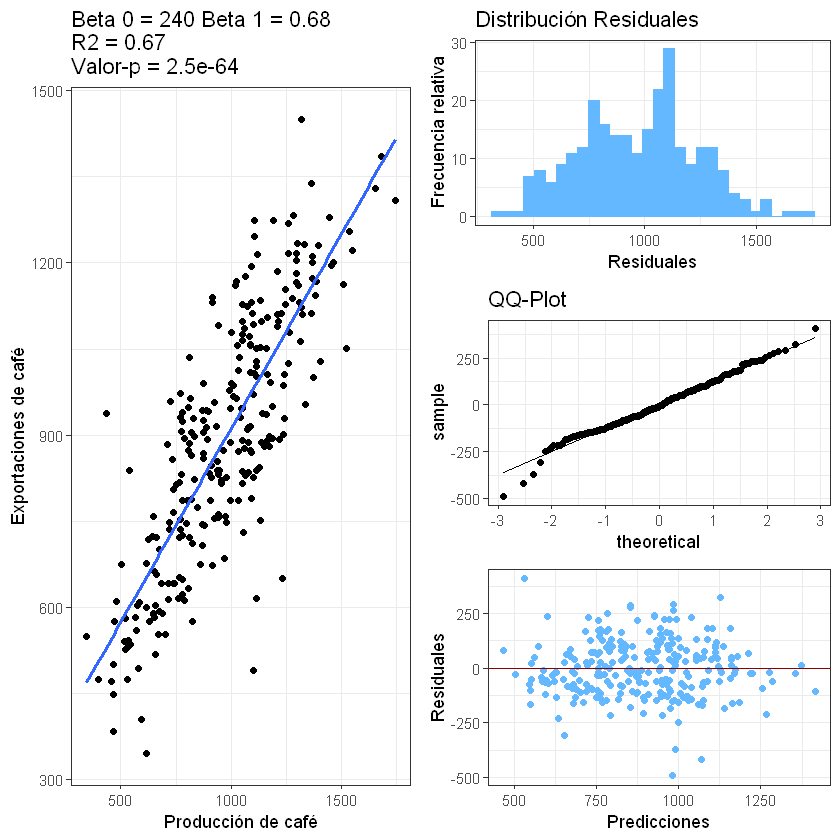
Parámetros de la regresión:

print(summary(regression)$coef)

               Estimate  Std. Error   t value     Pr(>|t|)
(Intercept) 235.3538372 29.77755312  7.903733 7.538088e-14
Producción    0.6768678  0.02961839 22.852960 2.530485e-64