ARIMA: autoregresivo integrado de medias móviles

Para series de tiempo no estacionarias.

La parte de integrado en ARIMA significa que se usará el número de diferencias no estacionales que debemos examinar para establecer estacionariedad. Los datos se transformará para que sean estacionarios. Esta transformación será con las diferencias \(\Delta x_t\).

ARIMA(p,d,q)

  • \(p\): Componente autoregresiva del modelo \((AR)\).

  • \(d\): orden de integración. Es el número de veces que se debe integrar la serie de tiempo para obtener la estacionariedad.

  • \(q\): Componente de medias móviles \((MA)\).

Los modelos ARIMA(p,d,q) son un modelo ARMA(p,q) aplicado a una nueva serie de tiempo generada mediante la integración, es decir, por las diferencias y que esta nueva serie de tiempo es estacionaria.

Se empezará con el modelo ARIMA(1,1,1), luego se analizan los residuos, si no son Ruido Blanco, se evalúan modelos más complejos.

Recordar que por cada integración se perderá una observación.

\(ARIMA(p,0,q)= ARMA(p,q)\)

ARIMA(1,1,1)

\[\Delta x_t = c+\varphi_1 \Delta x_{t-1}+\theta_1 \epsilon_{t-1}+\epsilon_t\]
\[\Delta x_t = x_t - x_{t-1}\]
import pandas as pd

datos = pd.read_csv('Precio.csv', sep=';', decimal=',')

datos.Fecha = pd.to_datetime(datos.Fecha, dayfirst = True)
datos.set_index('Fecha', inplace=True)

ARIMA(1,1,1)

from statsmodels.tsa.arima_model import ARIMA

import warnings
warnings.filterwarnings("ignore")

model_ar_1_i_1_ma_1 = ARIMA(datos.Precio, order=(1,1,1))
results_ar_1_i_1_ma_1 = model_ar_1_i_1_ma_1.fit()
results_ar_1_i_1_ma_1.summary()
ARIMA Model Results
Dep. Variable: D.Precio No. Observations: 5816
Model: ARIMA(1, 1, 1) Log Likelihood -27010.235
Method: css-mle S.D. of innovations 25.158
Date: Thu, 15 Jul 2021 AIC 54028.469
Time: 05:54:51 BIC 54055.143
Sample: 1 HQIC 54037.747
coef std err z P>|z| [0.025 0.975]
const 0.0408 0.364 0.112 0.911 -0.672 0.753
ar.L1.D.Precio -0.2638 0.059 -4.472 0.000 -0.379 -0.148
ma.L1.D.Precio 0.3930 0.056 7.080 0.000 0.284 0.502
Roots
Real Imaginary Modulus Frequency
AR.1 -3.7903 +0.0000j 3.7903 0.5000
MA.1 -2.5443 +0.0000j 2.5443 0.5000

Residuales del ARIMA(1,1,1)

import statsmodels.graphics.tsaplots as sgt
import matplotlib.pyplot as plt

residuos_ARIAM111 = results_ar_1_i_1_ma_1.resid
sgt.plot_acf(residuos_ARIAM111, zero = False, lags = 40)
plt.title("ACF Of Residuals for ARIMA(1,1,1)",size=20)
plt.show()
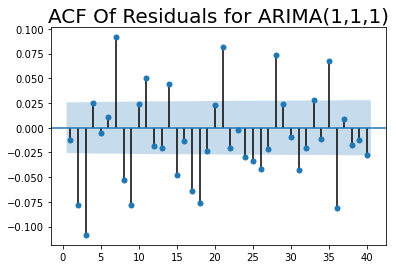
../_images/output_19_04.png 
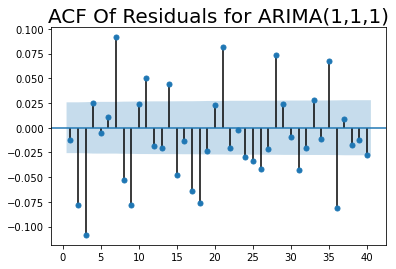
sgt.plot_acf(residuos_ARIAM111, zero = False, lags = 40)
plt.title("ACF Of Residuals for ARIMA(1,1,1)",size=20)
plt.show()
../_images/output_20_02.png

Evaluación de varios modelos de ARIMA

Primero se deben calcular todos los modelos y escoger los que tienen todos los coeficientes significativos. Este paso no se ha realizado, se evaluarán unos modelos que estamos suponiendo que tienen todos los coeficientes significativos.

model_ar_1_i_1_ma_2 = ARIMA(datos.Precio, order=(1,1,2))
results_ar_1_i_1_ma_2 = model_ar_1_i_1_ma_2.fit()
model_ar_1_i_1_ma_3 = ARIMA(datos.Precio, order=(1,1,3))
results_ar_1_i_1_ma_3 = model_ar_1_i_1_ma_3.fit()
model_ar_2_i_1_ma_1 = ARIMA(datos.Precio, order=(2,1,1))
results_ar_2_i_1_ma_1 = model_ar_2_i_1_ma_1.fit()
model_ar_3_i_1_ma_1 = ARIMA(datos.Precio, order=(3,1,1))
results_ar_3_i_1_ma_1 = model_ar_3_i_1_ma_1.fit()
model_ar_3_i_1_ma_2 = ARIMA(datos.Precio, order=(3,1,2))
results_ar_3_i_1_ma_2 = model_ar_3_i_1_ma_2.fit(start_ar_lags=5)

print("ARIMA(1,1,1):  \t LL = ", results_ar_1_i_1_ma_1.llf, "\t AIC = ", results_ar_1_i_1_ma_1.aic)
print("ARIMA(1,1,2):  \t LL = ", results_ar_1_i_1_ma_2.llf, "\t AIC = ", results_ar_1_i_1_ma_2.aic)
print("ARIMA(1,1,3):  \t LL = ", results_ar_1_i_1_ma_3.llf, "\t AIC = ", results_ar_1_i_1_ma_3.aic)
print("ARIMA(2,1,1):  \t LL = ", results_ar_2_i_1_ma_1.llf, "\t AIC = ", results_ar_2_i_1_ma_1.aic)
print("ARIMA(3,1,1):  \t LL = ", results_ar_3_i_1_ma_1.llf, "\t AIC = ", results_ar_3_i_1_ma_1.aic)
print("ARIMA(3,1,2):  \t LL = ", results_ar_3_i_1_ma_2.llf, "\t AIC = ", results_ar_3_i_1_ma_2.aic)

ARIMA(1,1,1):        LL =  -27010.234621625288       AIC =  54028.469243250576
ARIMA(1,1,2):        LL =  -26970.45408581454        AIC =  53950.90817162908
ARIMA(1,1,3):        LL =  -26951.814421818075       AIC =  53915.62884363615
ARIMA(2,1,1):        LL =  -26960.455943244346       AIC =  53930.91188648869
ARIMA(3,1,1):        LL =  -26954.471631818797       AIC =  53920.94326363759
ARIMA(3,1,2):        LL =  -26954.419566101034       AIC =  53922.83913220207

De los modelos evaluados, el mejor es el ARIMA(1,1,3) por tener mayor Log-Verosimilitud y menor AIC.

LLR Test

Sin embargo, los modelos ARIMA(1,1,1) y ARIMA(1,1,2) están anidados al modelo ARIMA(1,1,3), se hará comparación si el modelo ARIMA(1,1,3) es mejor que los dos anteriores.

def LLR_test(mod_1, mod_2, DF = 1):
    L1 = mod_1.llf
    L2 = mod_2.llf
    LR = (2*(L2-L1))
    p = chi2.sf(LR, DF).round(3)
    return p

from scipy.stats.distributions import chi2

print("\nLLR test p-value = " + str(LLR_test(results_ar_1_i_1_ma_2, results_ar_1_i_1_ma_3)))

LLR test p-value = 0.0

print("\nLLR test p-value = " + str(LLR_test(results_ar_1_i_1_ma_1, results_ar_1_i_1_ma_3, DF = 2)))

LLR test p-value = 0.0

El modelo ARIMA(1,1,3) si es mejor que los dos modelos que están anidados con este.

Residuales del modelo ARIMA(1,1,3)

residuales_ARIMA_113 = results_ar_1_i_1_ma_3.resid
sgt.plot_acf(residuales_ARIMA_113, zero = False, lags = 40)
plt.title("ACF Of Residuals for ARIMA(1,1,3)", size=20)
plt.show()
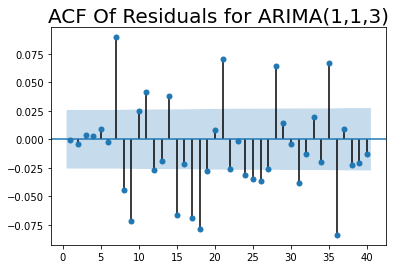
../_images/output_34_01.png

Se podría evaluar modelos más complejos hasta el ARIMA(7,1,7).

model_ar_5_i_1_ma_5 = ARIMA(datos.Precio, order=(5,1,5))
results_ar_5_i_1_ma_5 = model_ar_5_i_1_ma_5.fit(start_ar_lags=11)
results_ar_5_i_1_ma_5.summary()
ARIMA Model Results
Dep. Variable: D.Precio No. Observations: 5816
Model: ARIMA(5, 1, 5) Log Likelihood -26878.553
Method: css-mle S.D. of innovations 24.593
Date: Thu, 15 Jul 2021 AIC 53781.106
Time: 05:55:02 BIC 53861.127
Sample: 1 HQIC 53808.939
coef std err z P>|z| [0.025 0.975]
const 0.0411 0.332 0.124 0.901 -0.609 0.692
ar.L1.D.Precio -0.3205 0.042 -7.665 0.000 -0.402 -0.239
ar.L2.D.Precio -0.2270 0.033 -6.855 0.000 -0.292 -0.162
ar.L3.D.Precio -0.4506 0.030 -15.195 0.000 -0.509 -0.393
ar.L4.D.Precio -0.3947 0.034 -11.511 0.000 -0.462 -0.327
ar.L5.D.Precio -0.6894 0.032 -21.787 0.000 -0.751 -0.627
ma.L1.D.Precio 0.4184 0.040 10.561 0.000 0.341 0.496
ma.L2.D.Precio 0.1603 0.029 5.588 0.000 0.104 0.216
ma.L3.D.Precio 0.3645 0.027 13.655 0.000 0.312 0.417
ma.L4.D.Precio 0.4863 0.030 16.124 0.000 0.427 0.545
ma.L5.D.Precio 0.7429 0.029 25.497 0.000 0.686 0.800
Roots
Real Imaginary Modulus Frequency
AR.1 0.6833 -0.7607j 1.0225 -0.1335
AR.2 0.6833 +0.7607j 1.0225 0.1335
AR.3 -1.0478 -0.0000j 1.0478 -0.5000
AR.4 -0.4456 -1.0609j 1.1506 -0.3133
AR.5 -0.4456 +1.0609j 1.1506 0.3133
MA.1 0.6951 -0.7411j 1.0161 -0.1301
MA.2 0.6951 +0.7411j 1.0161 0.1301
MA.3 -1.0380 -0.0000j 1.0380 -0.5000
MA.4 -0.5034 -1.0013j 1.1207 -0.3241
MA.5 -0.5034 +1.0013j 1.1207 0.3241 
print("\nLLR test p-value = " + str(LLR_test(results_ar_1_i_1_ma_3, results_ar_5_i_1_ma_5)))

LLR test p-value = 0.0

El ARIMA(5,1,5) es mejor que el ARIMA(1,1,3)

Residuales del modelo ARIMA(5,1,5)

residuales_ARIMA_515 = results_ar_5_i_1_ma_5.resid
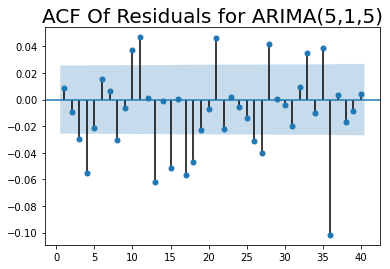
sgt.plot_acf(residuales_ARIMA_515, zero = False, lags = 40)
plt.title("ACF Of Residuals for ARIMA(5,1,5)", size=20)
plt.show()
../_images/output_40_01.png

Integración \(d\)

Se calculará la primer diferencia de los precios y se hará la prueba D-F para determinar si la nueva serie de tiempo es estacionaria o no.

Primera diferencia

datos['delta_prices']=datos.Precio.diff(1)

datos.head()
Precio delta_prices
Fecha
2003-03-01 72.412500 NaN
2003-03-02 72.837083 0.424583
2003-03-03 70.103750 -2.733333
2003-03-04 70.770417 0.666667
2003-03-05 69.153750 -1.616667 
import statsmodels.tsa.stattools as sts

sts.adfuller(datos.delta_prices[1:])

(-14.940985509998315,
 1.3227142701322909e-27,
 34,
 5781,
 {'1%': -3.431481673763484,
  '5%': -2.8620400923019074,
  '10%': -2.5670361971807805},
 53352.0028917936)

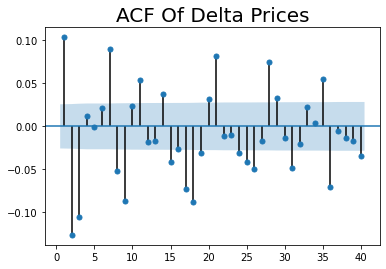
sgt.plot_acf(datos.delta_prices[1:], zero = False, lags = 40)
plt.title("ACF Of Delta Prices", size=20)
plt.show()
../_images/output_48_02.png 
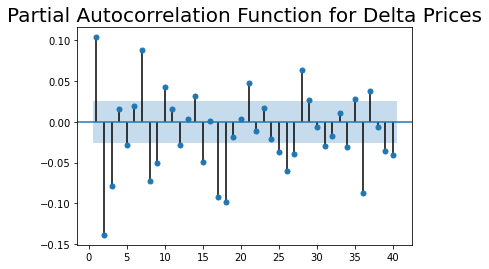
sgt.plot_pacf(datos.delta_prices[1:], lags = 40, alpha = 0.05, zero = False , method = ('ols'))
plt.title("Partial Autocorrelation Function for Delta Prices",size=20)
plt.show()
../_images/output_49_0.png

A continuación se mostrará una prueba de que una ARMA(1,1) sobre la primera diferencia de la serie de tiempo es igual a una ARIMA(1,1) sobre la serie de tiempo.

model_delta_ar_1_i_1_ma_1 = ARIMA(datos.delta_prices[1:], order=(1,0,1))
results_delta_ar_1_i_1_ma_1 = model_delta_ar_1_i_1_ma_1.fit()
results_delta_ar_1_i_1_ma_1.summary()
ARMA Model Results
Dep. Variable: delta_prices No. Observations: 5816
Model: ARMA(1, 1) Log Likelihood -27010.235
Method: css-mle S.D. of innovations 25.158
Date: Thu, 15 Jul 2021 AIC 54028.469
Time: 05:55:05 BIC 54055.143
Sample: 0 HQIC 54037.747
coef std err z P>|z| [0.025 0.975]
const 0.0408 0.364 0.112 0.911 -0.672 0.753
ar.L1.delta_prices -0.2638 0.059 -4.472 0.000 -0.379 -0.148
ma.L1.delta_prices 0.3930 0.056 7.080 0.000 0.284 0.502
Roots
Real Imaginary Modulus Frequency
AR.1 -3.7903 +0.0000j 3.7903 0.5000
MA.1 -2.5443 +0.0000j 2.5443 0.5000 
model_ar_1_i_1_ma_1 = ARIMA(datos.Precio, order=(1,1,1))
results_ar_1_i_1_ma_1 = model_ar_1_i_1_ma_1.fit()
results_ar_1_i_1_ma_1.summary()
ARIMA Model Results
Dep. Variable: D.Precio No. Observations: 5816
Model: ARIMA(1, 1, 1) Log Likelihood -27010.235
Method: css-mle S.D. of innovations 25.158
Date: Thu, 15 Jul 2021 AIC 54028.469
Time: 05:55:06 BIC 54055.143
Sample: 1 HQIC 54037.747
coef std err z P>|z| [0.025 0.975]
const 0.0408 0.364 0.112 0.911 -0.672 0.753
ar.L1.D.Precio -0.2638 0.059 -4.472 0.000 -0.379 -0.148
ma.L1.D.Precio 0.3930 0.056 7.080 0.000 0.284 0.502
Roots
Real Imaginary Modulus Frequency
AR.1 -3.7903 +0.0000j 3.7903 0.5000
MA.1 -2.5443 +0.0000j 2.5443 0.5000

SARIMA(p,d,q)(P,D,Q,s)

SARIMA-Seasonal Autoregressive Integrated Moving Averages

from statsmodels.tsa.statespace.sarimax import SARIMAX

model_sarima = SARIMAX(datos.Precio, order=(1,0,1), seasonal_order = (2,0,1,2))
results_sarima = model_sarima.fit()
results_sarima.summary()
SARIMAX Results
Dep. Variable: Precio No. Observations: 5817
Model: SARIMAX(1, 0, 1)x(2, 0, 1, 2) Log Likelihood -26974.805
Date: Thu, 15 Jul 2021 AIC 53961.610
Time: 05:55:09 BIC 54001.621
Sample: 0 HQIC 53975.526
- 5817
Covariance Type: opg
coef std err z P>|z| [0.025 0.975]
ar.L1 0.9949 0.001 1319.143 0.000 0.993 0.996
ma.L1 0.1061 0.003 40.096 0.000 0.101 0.111
ar.S.L2 0.8309 0.020 42.567 0.000 0.793 0.869
ar.S.L4 0.0987 0.004 22.085 0.000 0.090 0.108
ma.S.L2 -0.9498 0.019 -48.766 0.000 -0.988 -0.912
sigma2 623.3489 1.583 393.688 0.000 620.246 626.452
Ljung-Box (Q): 442.39 Jarque-Bera (JB): 19183877.49
Prob(Q): 0.00 Prob(JB): 0.00
Heteroskedasticity (H): 34.65 Skew: -6.00
Prob(H) (two-sided): 0.00 Kurtosis: 284.08


Warnings:
[1] Covariance matrix calculated using the outer product of gradients (complex-step).
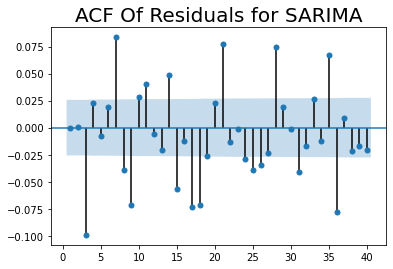
residuales_SARIMA = results_sarima.resid
sgt.plot_acf(residuales_SARIMA, zero = False, lags = 40)
plt.title("ACF Of Residuals for SARIMA", size=20)
plt.show()
../_images/output_57_0.png