Prueba de significancia de la regresión

Prueba de significancia de la regresión con el estadístico \(t\):

La significancia de la regresión se relaciona en determinar si la pendiente de la línea de regresión es significativa o no. La hipótesis nula \((H_0)\) es que la pendiente es igual a cero, es decir, que la pendiente no es significativa y no hay relación lineal entre \(X\) y \(y\) y que \(X\) tiene muy poco valor para explicar la variación de \(y\), en cambio, con la hipótesis alternativa \((H_1)\), se evalúa si la pendiente es diferente de cero, entonces, si existe una relación lineal entre \(X\) y \(y\).

Pruebas de hipótesis:

\[H_0: \beta_1 = 0\]
\[H_1: \beta_1 \neq 0\]

No rechazar \(H_0\) implica que la mejor estimación es \(\hat{y} = \overline{y}\) (Figura a) o que la relación no es lineal (Figura b).

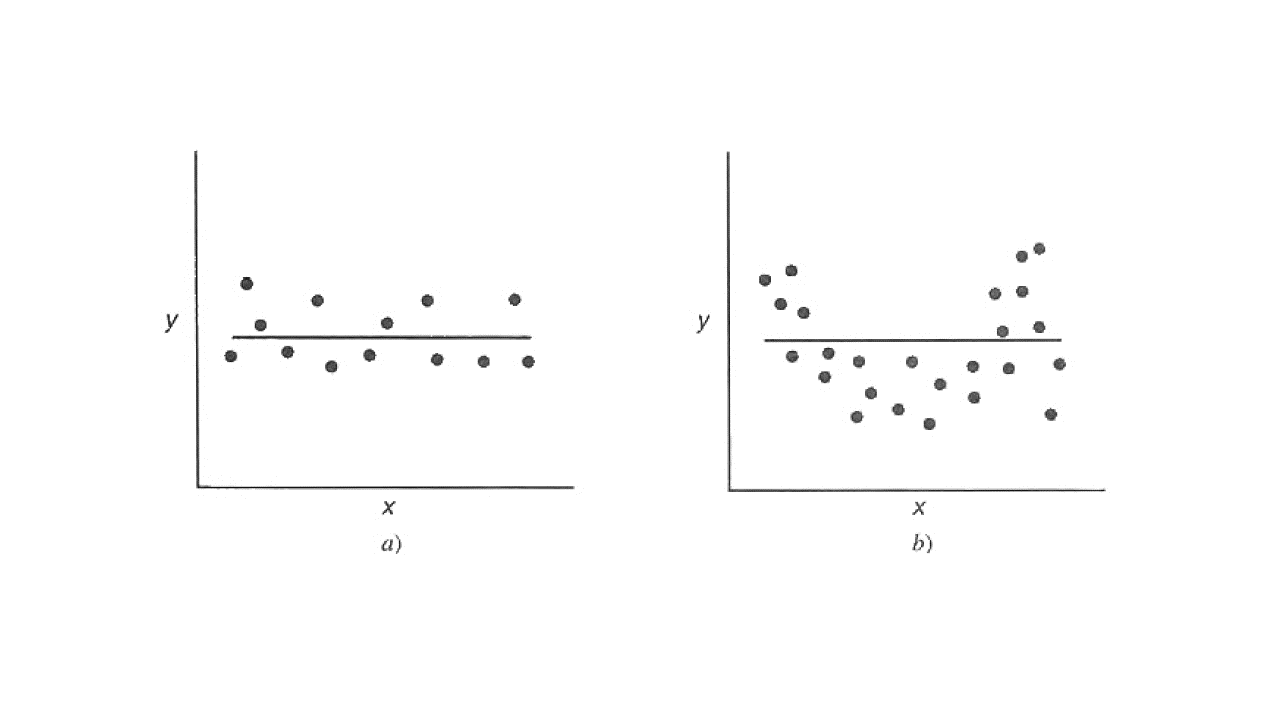
Significancia

Significancia

Fuente: Montgomery, Peck y Vining, 2001.

Al rechazar \(H_0\) implica que \(X\) sí pude explicar la variabilidad de \(y\). Si el modelo adecuado es como la Figura a; sin embargo, es posible que, aunque el modelo es significativo se podría tener mejores resultados con términos polinomiales en \(X\) como se muestra en la Figura b.

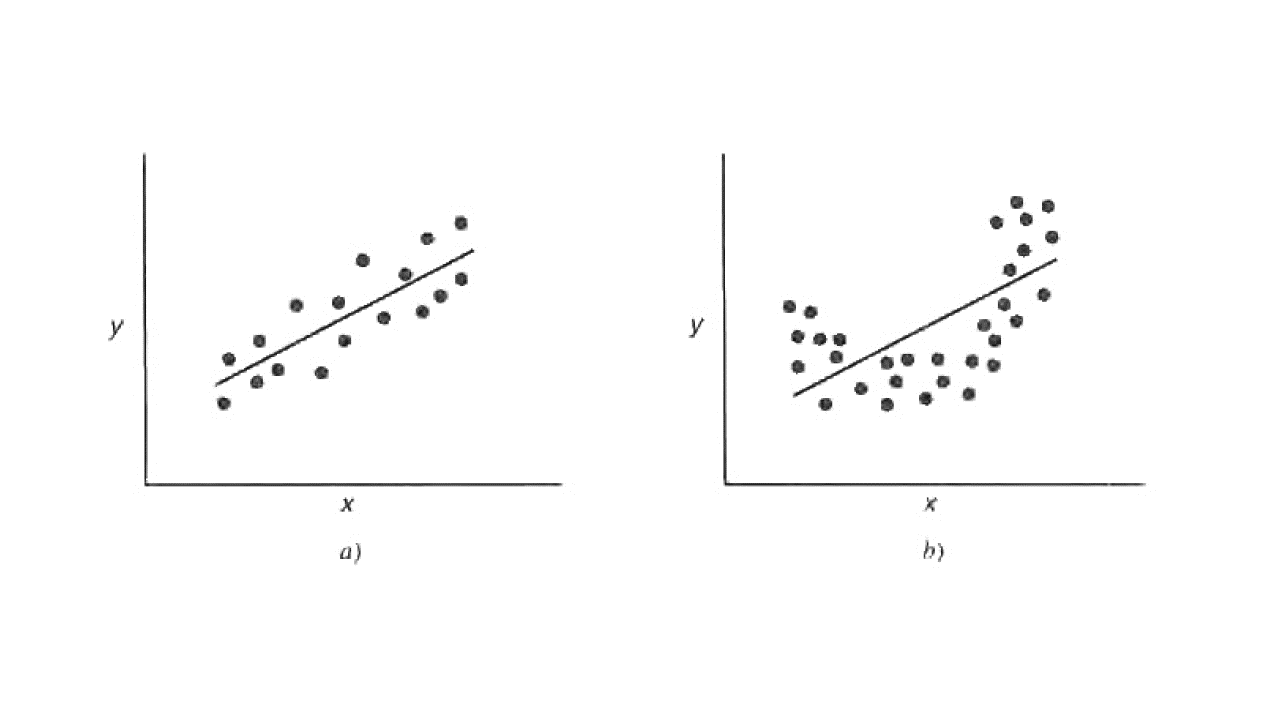
Linealidad

Linealidad

Fuente: Montgomery, Peck y Vining, 2001.

Se usa el estadístico \(t\) para determinar la significancia de la regresión así:

\[t_0 = \frac{\hat{\beta_1}}{SE(\hat{\beta_1})}\]

Donde,

\(SE(\hat{\beta_1})\): Es el error estándar de \(\hat{\beta_1}\).

\[SE(\hat{\beta_1}) = \sqrt{\frac{\sigma^2}{\sum_{}(X_i-\overline{X_i})^2}}\]

Donde \(\sigma^2\) es el cuadrado medio residual, es un estimador insesgado para la varianza de la regresión. \(\sigma\) es el error estándar de la regresión.

\[\sigma^2 = \frac{\sum_{}(y_i-\hat{y_i})^2}{n-2} = \frac{\sum_{} \hat{\varepsilon_i}^2}{n-2}\]

\(n-2\): son los grados de libertad del modelo df = n - 2. El 2 es porque se estiman dos parámetros.

Recuerde que: \(SSE = \sum_{} \hat{\varepsilon_i}^2 = \sum_{}(y_i-\hat{y_i})^2\), entonces:

\[\sigma^2 = \frac{SSE}{n-2}\]

Así que:

\[SE(\hat{\beta_1}) = \sqrt{\frac{\frac{SSE}{n-2}}{\sum_{}(X_i-\overline{X_i})^2}}\]

Se rechaza \(H_0\) cuando:

\[|t_0| > t_{\alpha/2, n – 2}\]

Donde,

\(t_{\alpha/2, n – 2}\): es el valor crítico de \(t\).

El \(t\) crítico se calcula en R así: qt(p = (1 - alfa) + alfa/2, df = n - 2)

Ejemplo: para un \(\alpha = 0,05\) y 264 datos n = 264, el \(t\) crítico es: 1.96905971525654

t_critico = qt(p = 0.95 + 0.05/2, df = n - 2)

Código en R:

datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))

       X PrecioInterno PrecioInternacional Producción Exportaciones     TRM
1 ene-00        371375              130.12        658           517 1923.57
2 feb-00        354297              124.72        740           642 1950.64
3 mar-00        360016              119.51        592           404 1956.25
4 abr-00        347538              112.67       1055           731 1986.77
5 may-00        353750              110.31       1114           615 2055.69
6 jun-00        341688              100.30       1092           869 2120.17
     EUR
1 1916.0
2 1878.5
3 1875.0
4 1832.0
5 1971.5
6 2053.5

X = datos$Producción
y = datos$Exportaciones

Ajuste del modelo:

regression <- lm(Exportaciones ~ Producción, data = datos)
regression

Call:
lm(formula = Exportaciones ~ Producción, data = datos)

Coefficients:
(Intercept)   Producción
   235.3538       0.6769

\(\hat{\beta_0}\):

beta_0 = as.numeric(regression$coefficients[1])
beta_0
235.353837174437

\(\hat{\beta_1}\):

beta_1 = as.numeric(regression$coefficients[2])
beta_1
0.676867843609397

Cantidad de datos \(n\):

n = length(X)
n
264

Residuales:

residuales = regression$residuals
head(residuales)
1
-163.732878269429
2
-94.236041445392
3
-232.059600591201
4
-218.449412182351
5
-374.384614955306
6
-105.493522395899

\(SE(\hat{\beta_1})\):

\[SE(\hat{\beta_1}) = \sqrt{\frac{\frac{SEE}{n-2}}{\sum_{}(X_i-\overline{X_i})^2}}\]
sqrt(sum(residuales^2)/(n-2)/sum((X-mean(X))^2))
0.0296183889365504

Estadístico \(t_0\) para \(\hat{\beta_1}\):

\[t_0 = \frac{\hat{\beta_1}}{SE(\hat{\beta_1})}\]
t_0 = beta_1/sqrt(sum(residuales^2)/(n-2)/sum((X-mean(X))^2))
t_0
22.8529595265769

\(t\) crítico:

t_critico = qt(p = 0.95 + 0.05/2, df = n - 2)
t_critico
1.96905971525654

Prueba de hipótesis:

\[|t_0| > t_{\alpha/2, n – 2}\]
\[|22,85| > 1,97\]
if(abs(t_0) > t_critico) {"Se acepta"} else {"Se rechaza"}
'Se acepta'

En el summary() aparecen los errores estándar SE de valor del \(\beta_0\) y \(\beta_1\) y los estadísticos \(t\) de cada uno.

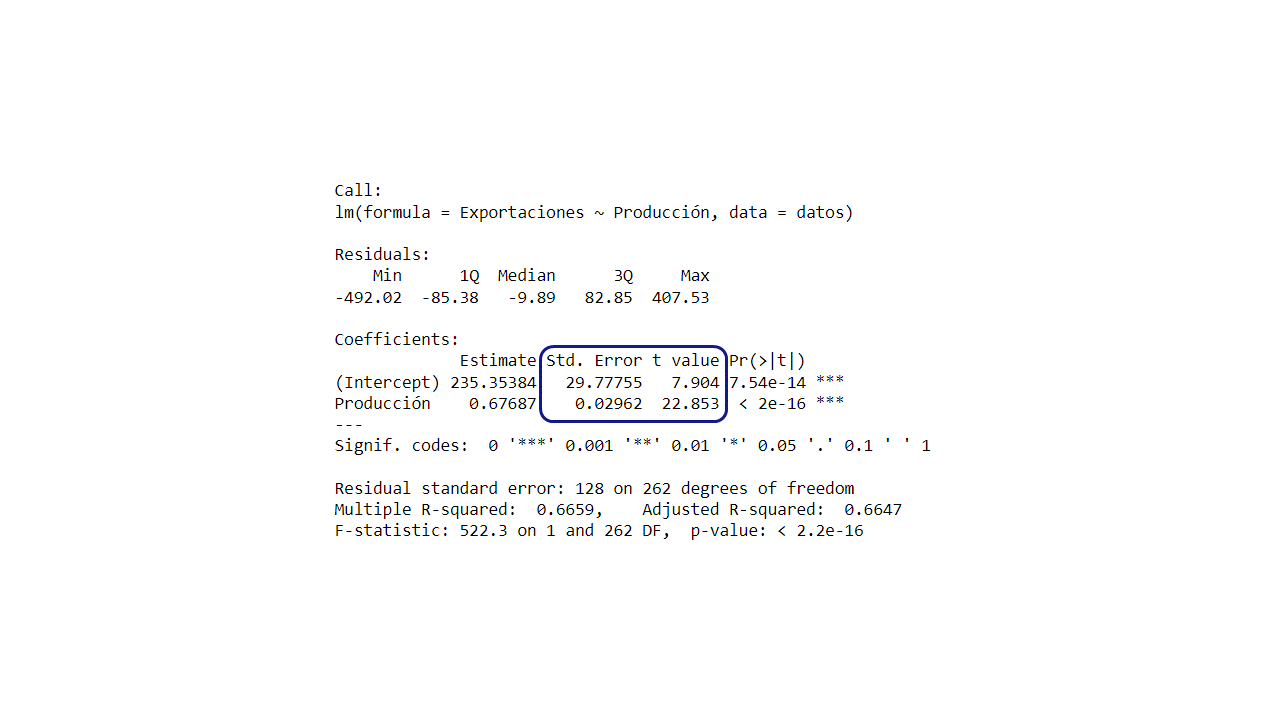
Estadístico

Estadístico

summary(regression)

Call:
lm(formula = Exportaciones ~ Producción, data = datos)

Residuals:
    Min      1Q  Median      3Q     Max
-492.02  -85.38   -9.89   82.85  407.53

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) 235.35384   29.77755   7.904 7.54e-14 *
Producción    0.67687    0.02962  22.853  < 2e-16 *
---
Signif. codes:  0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 128 on 262 degrees of freedom
Multiple R-squared:  0.6659,        Adjusted R-squared:  0.6647
F-statistic: 522.3 on 1 and 262 DF,  p-value: < 2.2e-16

Prueba de significancia de la regresión con el \(valor-p\):

Otra forma para determinar la significancia del modelo es usando el \(valor- p\). El summary() ya lo tiene calculado y por medio de asteriscos indica si los parámetros son significativos o no, entre más asteriscos es más significativo

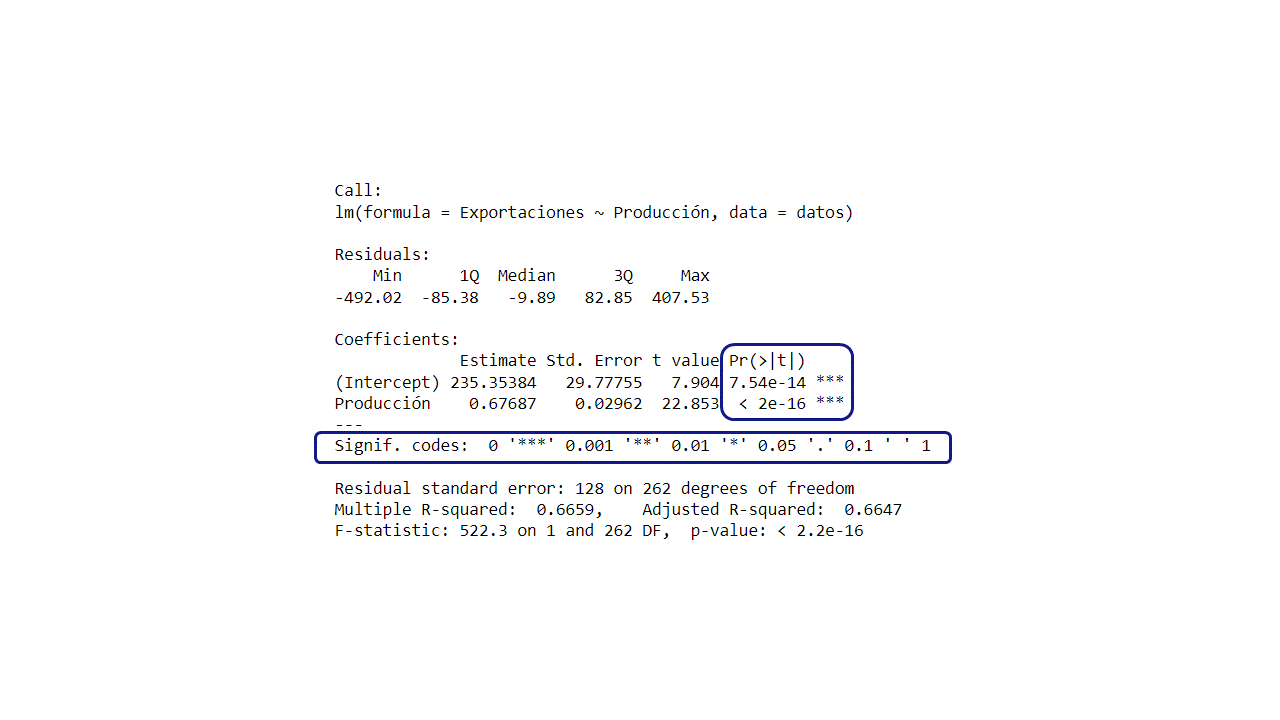
p-value

p-value