Análisis de Normalidad en RLS

La línea de regresión estimada es la mejor aproximación de la relación entre $X$ y $y$, pero podemos agregar un término probabilístico que representará la incertidumbre de la línea recta y se llamará el error $(\varepsilon)$.

\[\hat{y_i} = \hat{\beta_0}+\hat{\beta_1}X_i+\hat{\varepsilon_i}\]

\[\hat{\varepsilon_i} = y_i-\hat{y_i}\]

$\hat{\varepsilon_i}$: también llamado residuales.

El error es la comparación entre el valor real $(y_i)$ y el valor predicho $(\hat{y_i})$. Son las distancias verticales de la siguiente Figura.

La letra Griega ${\varepsilon_i}$ (sin el $\hat{}$) se llama error de predicción y se representa con la ecuación: $\varepsilon_i=y_i-\overline{y_i}$. Note que en esta ecuación se usa $\overline{y_i}$ en lugar de $\hat{y_i}$.

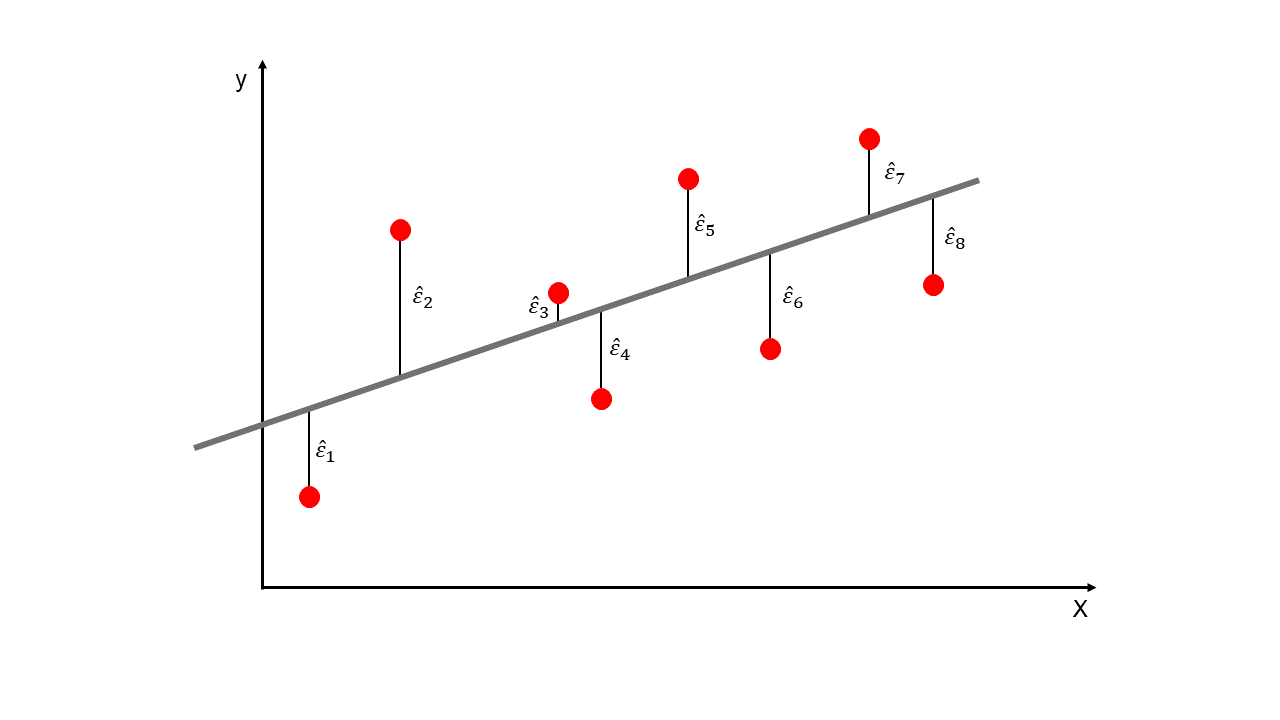
Residuales

Supuestos de la Regresión Lineal Simple:

Independencia: los errores de la predicción, $\varepsilon_i$, son estadisticamente independientes entre si.
Homocedasticidad (varianza constante): la varianza de los errores es constante a los largo de la distribución $X$. Lo contrario se llama heterocedasticidad.
Normalidad: los errores son una variable aleatoria normalmente distribuida con media igual a cero. $\varepsilon_i \sim N(0,\sigma^2)$.
Linealidad: el valor medio de $y$ es una función lineal de $X$, es decir, $y$ y $X$ tienen una relación lineal.

Los tres primeros supuestos anteriores se pueden resumir de la siguiente manera:

\[\varepsilon_i \sim^{iid}N(0,\sigma^2)\]

$iid$: los errores son independientes e idénticamente distribuidos. Con esta expresión se mencionan los tres supuestos: independencia, homocedasticidad y distribución de los errores.

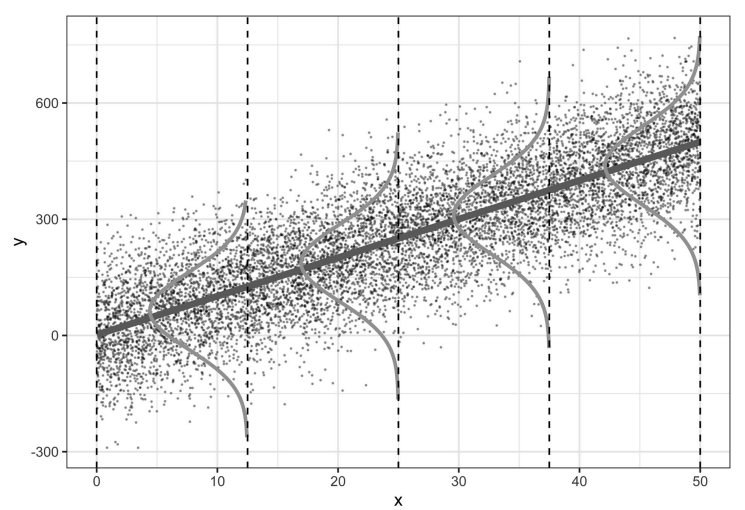Supuestos Fuente: Roback y Legler, 2021.

QQ-Plot:

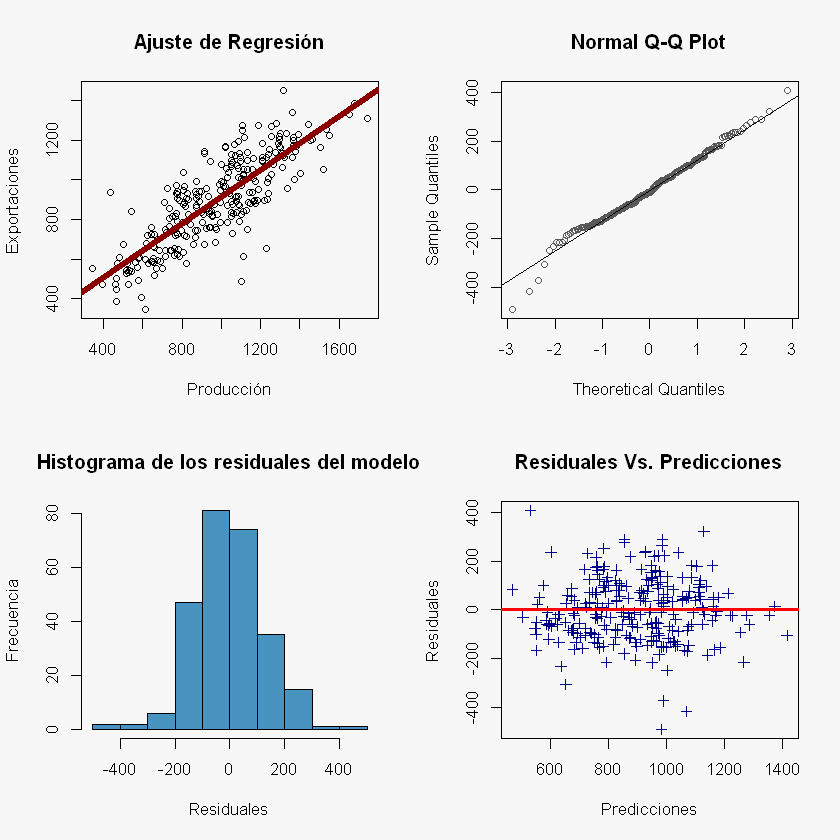
Los residuales son una medida de la variabilidad de la variable $y$ que no es explicada en el modelo de regresión. Con el análisis de los residuales se puede determinar los adecuado o inadecuado del modelo, en otras palabras, es una forma efectiva de concluir el nivel de ajuste del modelo a los datos. Así que el análisis gráfico de los residuales es una forma efectiva de comprobar el adecuado ajuste del modelo de regresión.

Las pequeñas desviaciones con respecto a la hipótesis de normalidad de los residuales no afectan mucho al modelo, pero una no normalidad grande si lo es. Si la distribución de los residuales tiene colas pesadas, el ajuste por mínimos cuadrado es muy sensible a cambio en el subconjunto de datos. Para comprobar la hipótesis de normalidad de manera rápida es trazar la gráfica de normalidad de los residuales donde los cuantiles de la distribución normal aparecen en línea recta y los puntos de los residuales debería aproximarse a esta línea recta. En análisis de este gráfico se centra en los valores centrales y no en los extremos. Las grandes diferencias entre los puntos de los residuales y la línea recta que representa la distribución normal indican que los errores no siguen una distribución normal.Este gráfico se llama QQ-Plot.

La Figura 1 es el ideal de un ajuste a distribución normal, las demás figuras presentan problemas particulares como los siguientes:

Figura 2: Las dos colas de la distribución son demasiado gruesas (Fail Tails).
Figura 3: Colas delgadas.
Figura 4: Asimetría positiva.
Figura 5: Asimetría negativa.

En este gráfico se puede identificar puntos atípicos en los datos.

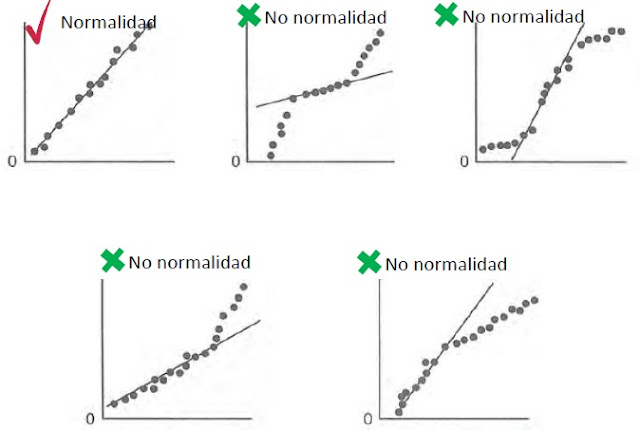
Normalidad

Fuente: Montgomery, Peck y Vining, 2001.

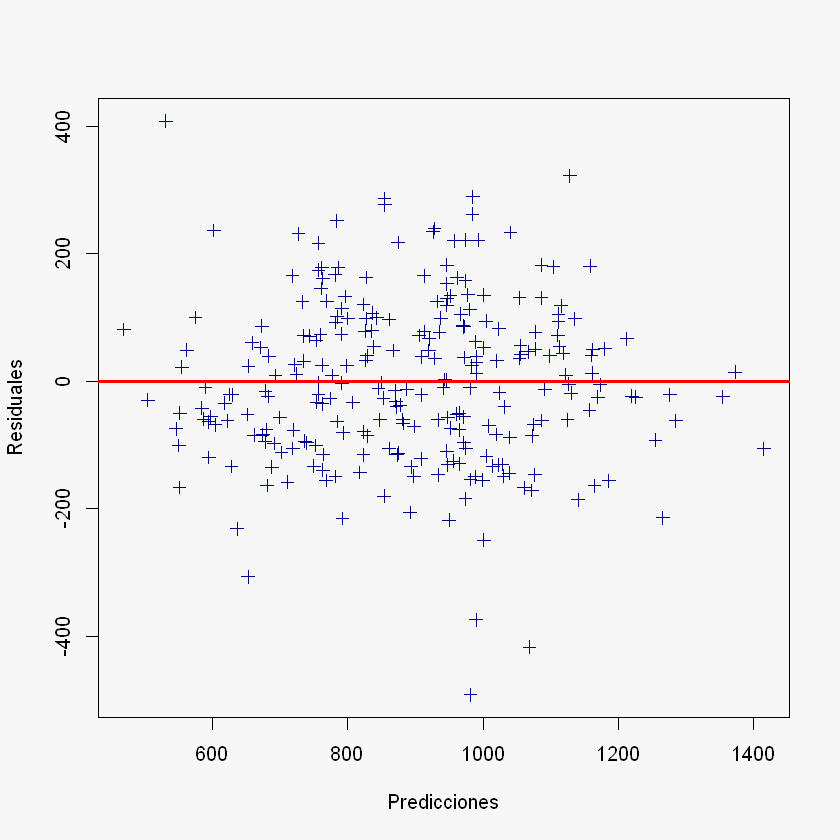
Gráfico de Residuales con respecto a las predicciones:

En este gráfico se analiza la dispersión de los errores con respecto a la media que es igual a cero. Para tener un comportamiento normal se espera que la nube de puntos esté encerrada en un rectángulo como se muestra en la Figura 1 (homocedasticidad), el resultado es que el modelo de regresión es adecuado. Los demás patrones que aparecen en las demás figuras son síntomas de deficiencias del modelo.

Figura 2: Varianza no constante y creciente (heterocedasticidad).
Figura 3: Varianza no constante (heterocedasticidad).
Figura 4: No linealidad.

En este gráfico también se puede identificar puntos atípicos.

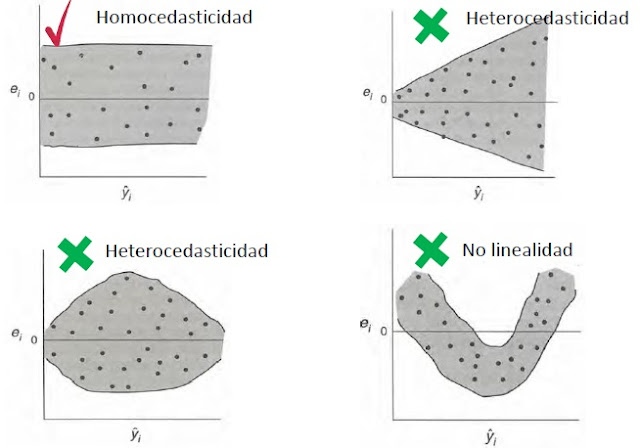
Homocedasticidad

Fuente: Montgomery, Peck y Vining, 2001.

Código en R:

datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))

   Fecha PrecioInterno PrecioInternacional Producción Exportaciones     TRM
ene-00        371375              130.12        658           517 1923.57
feb-00        354297              124.72        740           642 1950.64
mar-00        360016              119.51        592           404 1956.25
abr-00        347538              112.67       1055           731 1986.77
may-00        353750              110.31       1114           615 2055.69
jun-00        341688              100.30       1092           869 2120.17
     EUR
1916.0
1878.5
1875.0
1832.0
1971.5
2053.5

X = datos$Producción
y = datos$Exportaciones

Ajuste del modelo:

regression <- lm(Exportaciones ~ Producción, data = datos)
regression

Call:
lm(formula = Exportaciones ~ Producción, data = datos)

Coefficients:
(Intercept)   Producción
   235.3538       0.6769

summary(regression)

Call:
lm(formula = Exportaciones ~ Producción, data = datos)

Residuals:
    Min      1Q  Median      3Q     Max
-492.02  -85.38   -9.89   82.85  407.53

Coefficients:
             Estimate Std. Error t value Pr(>|t|)
(Intercept) 235.35384   29.77755   7.904 7.54e-14 *
Producción    0.67687    0.02962  22.853  < 2e-16 *
---
Signif. codes:  0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 128 on 262 degrees of freedom
Multiple R-squared:  0.6659,        Adjusted R-squared:  0.6647
F-statistic: 522.3 on 1 and 262 DF,  p-value: < 2.2e-16

$\hat{\beta_0}$:

beta_0 = as.numeric(regression$coefficients[1])
beta_0

235.353837174437

$\hat{\beta_1}$:

beta_1 = as.numeric(regression$coefficients[2])
beta_1

0.676867843609397

Cálculo de los residuales:

\[\hat{\varepsilon_i} = y_i-\hat{y_i}\]

y_pred = regression$fitted.values
print(head(y_pred))

       1        2        3        4        5        6
680.7329 736.2360 636.0596 949.4494 989.3846 974.4935

residuales = y - y_pred
head(residuales)

1: -163.732878269429
2: -94.2360414453919
3: -232.0596005912
4: -218.449412182351
5: -374.384614955306
6: -105.493522395899

Otra forma de extraer los residuales es: $residuals

head(regression$residuals)

1: -163.732878269429
2: -94.236041445392
3: -232.059600591201
4: -218.449412182351
5: -374.384614955306
6: -105.493522395899

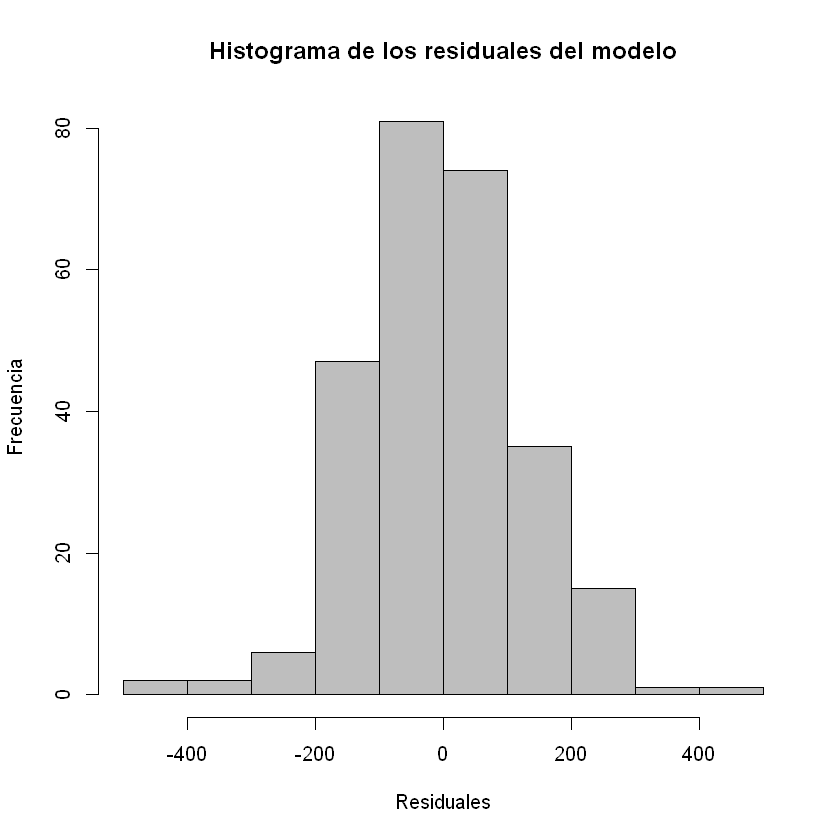
Histograma de los residuales:

hist(residuales, col = "gray", xlab = "Residuales", ylab = "Frecuencia",
    main = "Histograma de los residuales del modelo")

QQ-Plot:

qnorm(residuales): grafica los puntos.
qqline(residuales): grafica la línea recta que representa la distribución normal.

qqnorm(residuales)
qqline(residuales)

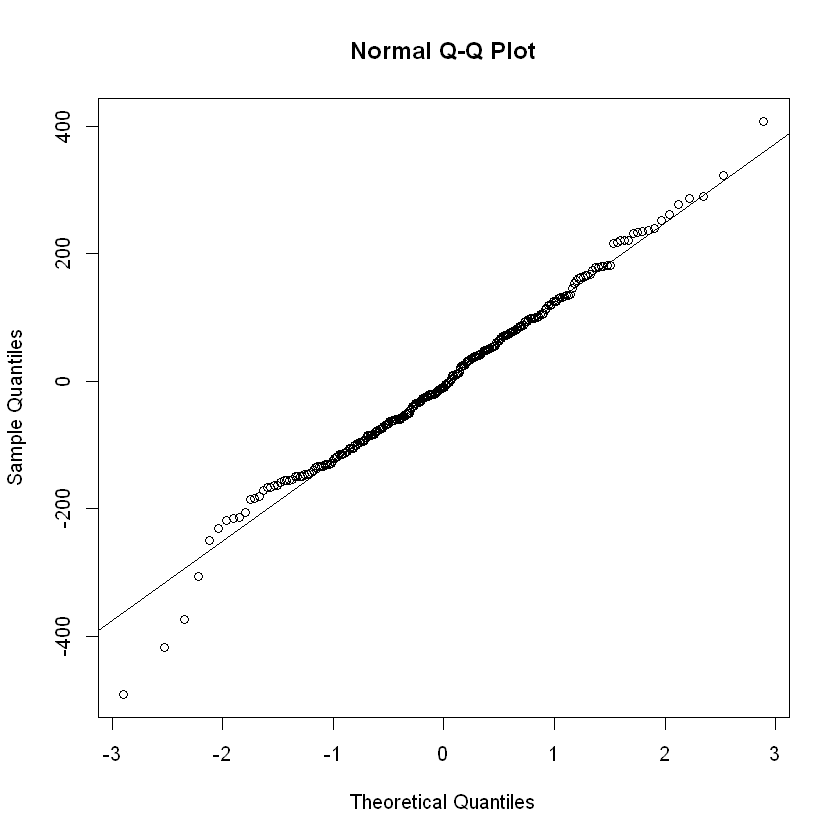
Gráfico de Residuales con respecto a las predicciones:

par(bg = "#f7f7f7")
plot(y_pred, residuales,
    xlab = "Predicciones",
    ylab = "Residuales",
    col = "darkblue",
    pch = 3)
abline(h = 0, col = "red", lwd = 3)

Gráficos del modelo de RLS:

layout(matrix(c(1:4), 2,2))
# layout.show(4)  correr esta línea en RStudio. Para quitar la particion correr: dev.off()

par(bg = "#f7f7f7")
plot(X, y,
    xlab = "Producción",
    ylab = "Exportaciones",
    main = "Ajuste de Regresión")
abline(beta_0, beta_1, col = "darkred", lwd = 5)

hist(residuales, col = "#4993C0", xlab = "Residuales", ylab = "Frecuencia",
    main = "Histograma de los residuales del modelo")

qqnorm(residuales, col = "#585858")
qqline(residuales)

par(bg = "#f7f7f7")
plot(y_pred, residuales,
    xlab = "Predicciones",
    ylab = "Residuales",
    col = "darkblue",
    pch = 3,
    main = "Residuales Vs. Predicciones")
abline(h = 0, col = "red", lwd = 3)