Taller Intervalos de Confianza y Pruebas de Hipótesis

Importar datos:

america=read.csv("america.csv", sep = ",", dec = ".")
asia=read.csv("asia.csv", sep = ",", dec = ".")
str(america)
str(asia)

'data.frame':       43 obs. of  3 variables:
 $ X        : int  14 16 18 20 22 36 58 64 80 82 ...
 $ SALESORG : Factor w/ 1 level "AMER": 1 1 1 1 1 1 1 1 1 1 ...
 $ NETAMOUNT: num  61392 18545 65825 24076 332 ...
'data.frame':       77 obs. of  3 variables:
 $ X        : int  5 7 9 17 23 27 31 37 41 43 ...
 $ SALESORG : Factor w/ 1 level "EMEA": 1 1 1 1 1 1 1 1 1 1 ...
 $ NETAMOUNT: num  62724 152239 111828 35605 6081 ...

Tamaño de muestras:

nx=nrow(america)
ny=nrow(asia)

alpha=0.05
p_alpha=qnorm(alpha) #probabilidad de la normal

Medias y desviaciones estándar:

media_x=mean(america$NETAMOUNT)
media_y=mean(asia$NETAMOUNT)
sd_x= sd(america$NETAMOUNT)
sd_y= sd(asia$NETAMOUNT)

QQ-plot:

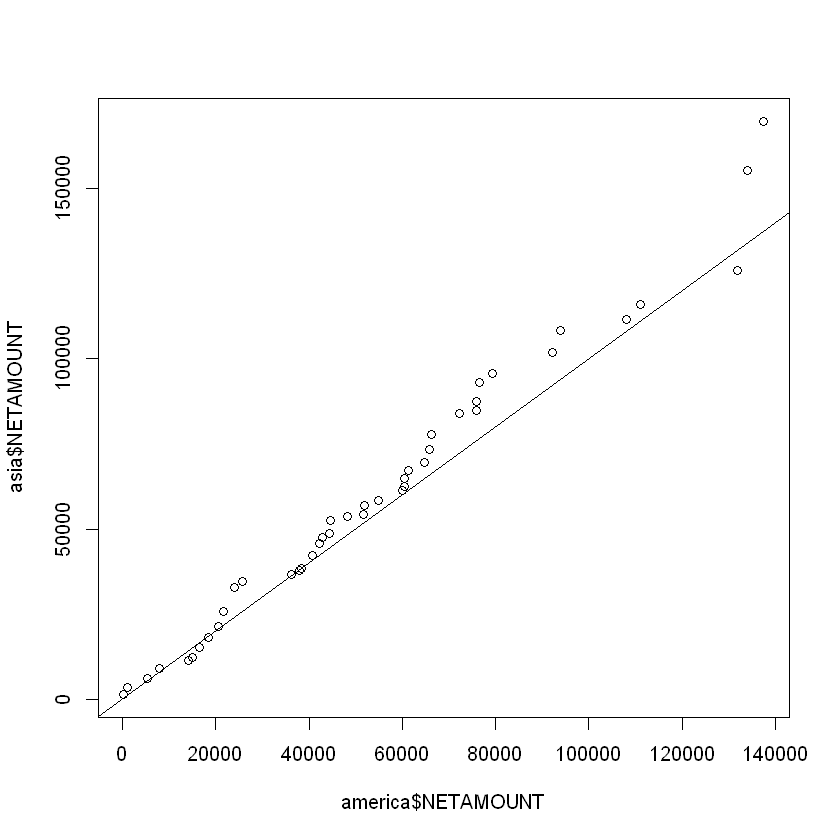
qqplot(america$NETAMOUNT, asia$NETAMOUNT)
abline(0,1) # las muestras parecen provenir de la misma distribución,
            # podemos asumirlas como normales

La función t.test de la libreria stats se utiliza para calcular intervalos de confianza para la media y diferencia de medias, con muestras independientes y pareadas.

Para una población:

print(t.test(x=america$NETAMOUNT, conf.level=0.95)$conf.int)

[1] 43338.84 65191.48
attr(,"conf.level")
[1] 0.95

Para la diferencia de medias:

Se requiere definir mínimo los siguientes argumentos: x, y, paired=T (si son datos pareados), paired= F (si nos son pareados)-

var.equal: indica que las varianzas son desconocidas y diferentes, si la varianzas se pueden considerar iguales se coloca var.equal=TRUE

conf.level:

print(t.test(x=america$NETAMOUNT, y=asia$NETAMOUNT,
             paired=FALSE, var.equal=FALSE,
             conf.level = 0.95)$conf.int)

[1] -19302.818   8539.797
attr(,"conf.level")
[1] 0.95

Intervalo de confianza unilateral para la media:

Para modificar la cola de intervalo se cambia el argumento alternative=less (si se quiere cola izquierda) o =greater(para la cola derecha).

print(t.test(america$NETAMOUNT, alternative = "less", conf.level = 0.95)$conf.int)

[1]     -Inf 63371.61
attr(,"conf.level")
[1] 0.95

Intervalos de proporciones:

¿Cuántas ventas superan los 55.000 USD en america?

exito= nrow(subset(america, NETAMOUNT >= 55000))
total= nrow(america)

p_muestra= exito/total

print(prop.test(x=exito, n=total, conf.level=0.95)$conf.int)

[1] 0.2940528 0.5999197
attr(,"conf.level")
[1] 0.95

Si se quiere realiza la diferencia se proporciones los argumentos x y n se deben colocar como vectores; por ejemplo: x=c(80,50), n=c(500, 1000).

Si se cambia el argumento alternative, se cambia la lateralidad: alternative=c("two.sided", "less", "greater").

Pruebas de hipótesis:

Media \(\mu\) de una población normal:

\[H0 : \mu =50000\]

\[H1 : \mu <> 500\]

Para esta hipótesis debe colocarse el argumento alternative= "two.sided"

t.test(america$NETAMOUNT, alternative='two.sided',
       conf.level=0.95, mu=54261)

    One Sample t-test

data:  america$NETAMOUNT
t = 0.00076833, df = 42, p-value = 0.9994
alternative hypothesis: true mean is not equal to 54261
95 percent confidence interval:
 43338.84 65191.48
sample estimates:
mean of x
 54265.16

Intervalo para comparación de varianzas prueba F:

print(var.test(america$NETAMOUNT, asia$NETAMOUNT, conf.level = 0.95)$conf.int)

[1] 0.4913745 1.4438581
attr(,"conf.level")
[1] 0.95

Prueba de hipótesis para una proporción:

Asumiremos una proporción poblacional del 50% ya que no contamos con un estudio previo.

\[H0: P=0.5\]

\[H1: P \neq 0.5\]

prop.test(exito, total, p =0.5,alternative = c("two.sided"), conf.level = 0.95, correct = TRUE)

    1-sample proportions test with continuity correction

data:  exito out of total, null probability 0.5
X-squared = 0.37209, df = 1, p-value = 0.5419
alternative hypothesis: true p is not equal to 0.5
95 percent confidence interval:
 0.2940528 0.5999197
sample estimates:
        p
0.4418605

Prueba de hipótesis para las diferencias de medias:

\[H0: \mu_x - \mu_y=40000\]

\[H1: \mu_x - \mu_y \neq 40000\]

t.test(x=america$NETAMOUNT, y=asia$NETAMOUNT, alternative="two.sided", mu=40000,
       paired=FALSE, var.equal=TRUE, conf.level=0.95)

    Two Sample t-test

data:  america$NETAMOUNT and asia$NETAMOUNT
t = -6.297, df = 118, p-value = 5.386e-09
alternative hypothesis: true difference in means is not equal to 40000
95 percent confidence interval:
 -19652.919   8889.898
sample estimates:
mean of x mean of y
 54265.16  59646.67

Prueba de hipótesis para diferencias de varianza:

var.test(x=america$NETAMOUNT, y=asia$NETAMOUNT, alternative = "two.sided",
         null.value = 1, conf.level = 0.95)

    F test to compare two variances

data:  america$NETAMOUNT and asia$NETAMOUNT
F = 0.8247, num df = 42, denom df = 76, p-value = 0.5012
alternative hypothesis: true ratio of variances is not equal to 1
95 percent confidence interval:
 0.4913745 1.4438581
sample estimates:
ratio of variances
         0.8247037

Taller:

Responda las siguientes preguntas haciendo uso de los mismos datos, y argumente su respuesta.

Indique si se puede establecer con un 90% de confianza que las ventas promedio de bicicletas en Asia son de 19500 USD.
Vamos a asumir que las muestras de Asia y América son pareadas, por tanto, borraremos las ultimas filas en Asia que no cuentan con su respectivo par en América:

asia_par=asia[-c(44:77),] Para que ambas muestras quedarán con 43 datos.

Calcule el IC para las muestras pareadas e indique las diferencias con el intervalo con muestras independientes.

Se puede decir que un nivel del 90% de confianza para las ventas de bicicletas en Asia superarán los 45000 USD.
El director financiero de la regional de Asia le pide comprobar con un nivel de significancia del 10%, si las ventas medias son inferiores a 30.000 USD donde incurrirá en pérdidas.
Argumente si las muestras pareadas de las regiones de Asia y América pueden ser menores de 50000 USD a un nivel de significancia del 95%.