Medidas de desempeño RLS
Las siguientes métricas se relacionan con los residuales y entre más bajo la métrica mejor porque error sería bajo. En algunos casos, como en los métodos de Machine Learning al resultado del error se le llama pérdida (loss) o costo (cost).
Máximo Error.
Error Medio Absoluto (MSE).
Error Porcentual Absoluto Medio (MAPE).
Por su parte, el coeficiente de determinación \((R^2)\) es una medida de cuánto son explicados los datos con el modelo de regresión ajustado. Entre más cercano a uno es mejor.
Código en R:
datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))
X PrecioInterno PrecioInternacional Producción Exportaciones TRM
1 ene-00 371375 130.12 658 517 1923.57
2 feb-00 354297 124.72 740 642 1950.64
3 mar-00 360016 119.51 592 404 1956.25
4 abr-00 347538 112.67 1055 731 1986.77
5 may-00 353750 110.31 1114 615 2055.69
6 jun-00 341688 100.30 1092 869 2120.17
EUR
1 1916.0
2 1878.5
3 1875.0
4 1832.0
5 1971.5
6 2053.5
X = datos$Producción
y = datos$Exportaciones
Ajuste del modelo:
regression <- lm(Exportaciones ~ Producción, data = datos)
regression
Call:
lm(formula = Exportaciones ~ Producción, data = datos)
Coefficients:
(Intercept) Producción
235.3538 0.6769
\(\hat{\beta_0}\):
beta_0 = as.numeric(regression$coefficients[1])
beta_0
\(\hat{\beta_1}\):
beta_1 = as.numeric(regression$coefficients[2])
beta_1
Cálculo de los residuales:
residuales = regression$residuals
head(residuales)
- 1
- -163.732878269429
- 2
- -94.236041445392
- 3
- -232.059600591201
- 4
- -218.449412182351
- 5
- -374.384614955306
- 6
- -105.493522395899
Métricas para evaluar el desempeño del modelo:
Error Máximo:
De los residuos se selecciona el mayor.
Entre más bajo el resultado, mejor.
max_error = max(residuales)
max_error
Error Medio Absoluto - MSE:
En inglés Mean Squared Error - MSE. Es el promedio de los residuos con los cuales se aplicó OLS.
El MSE es últil para comparar diferentes modelos.
Esta métrica no es sensible a los outliers.
Entre más bajo el resultado, mejor.
MSE = mean(residuales^2)
MSE
Error Porcentual Absoluto Medio - MAPE:
En inglés Mean Absolute Percentage Error - MAPE.
Entre más bajo el resultado, mejor.
MAPE = mean(abs(residuales/y))
MAPE
Coeficiente de Determinación \(R^2\):
Es una versión estandarizada del MSE. El \(R^2\) es la fracción de la varianza de \(y\) que es capturada por el modelo, es decir, cuánto de la varianza de \(y\) es explicada por la variable \(X\). El resultado está entre cero y uno, pero en pocos casos puede dar negativo particularmente cuando se trabaja con conjuntos de prueba (test).
Donde,
\(SSE = \sum_{} \hat{\varepsilon_i}^2 = \sum_{}(y_i-\hat{y_i})^2\)
\(SST = \sum_{}(y_i-\overline{y_i})^2\). Note que se utiliza \(\overline{y_i}\) en lugar de \(\hat{y_i}\).
\(SST = \sigma_y^2\)
Entonces,
Entre más cercano a uno el resultado, mejor.
Con el Coeficiente de Determinación \(R^2\) se analiza lo siguiente:
\(SST\) es una medida de la variabilidad de \(y\) sin considerar la variable regresora \(X\) y \(SSE\) es una medida de la variabilidad de \(y\) considerando \(X\). Entonces, entre mayor sea \(SSE\) que \(SST\) el modelo es mejor porque se estaría indicando que la mayor parte de la variabilidad de \(y\) se está explicando con el modelo de regresión. Como \(0<=SSE<=SST\), entonces \(0<=R^2<=1\).
En otras la palabras, el \(R^2\) hace una comparación entre modelar \(y\) con una línea recta igual a \(\overline{y}\) que su pendiente es cero o con una línea recta de la forma \(\hat{y_i} = \hat{\beta_0}+\hat{\beta_1}X_i\)
R_2 = 1 - mean(residuales^2)/var(y)
R_2
En el summary() aparece calculado el \(R^2\).
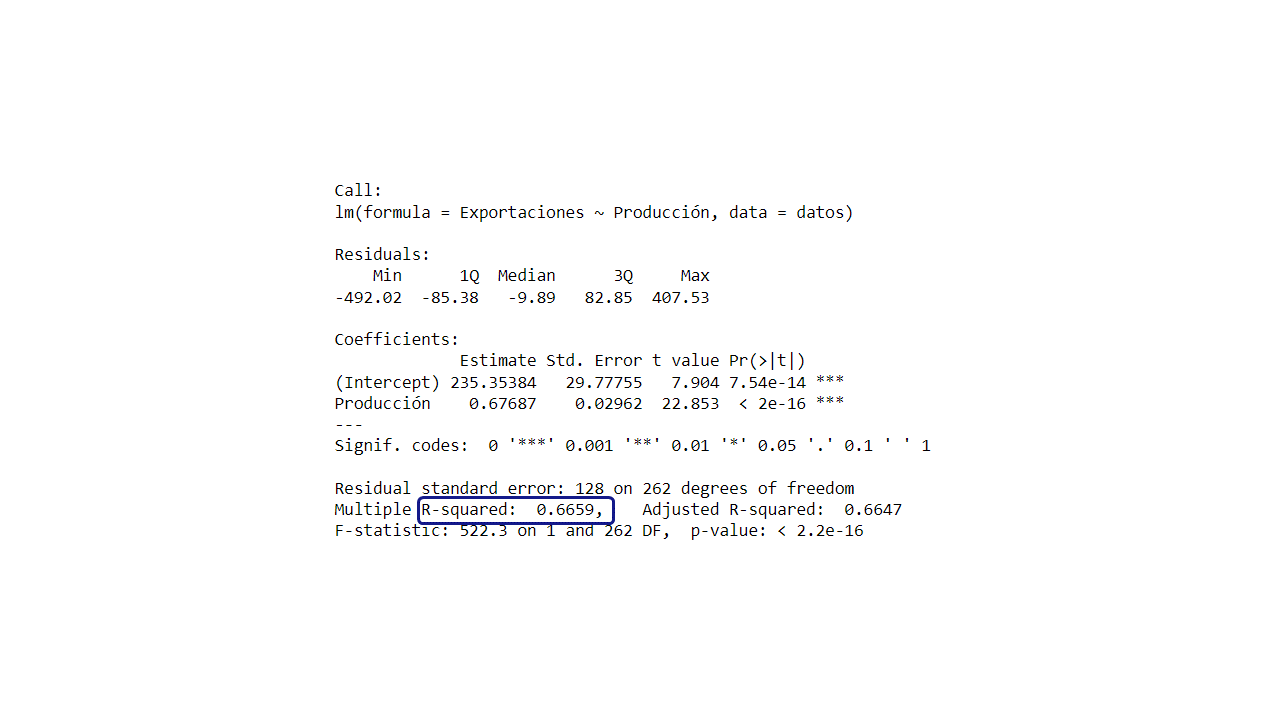
R2
summary(regression)
Call:
lm(formula = Exportaciones ~ Producción, data = datos)
Residuals:
Min 1Q Median 3Q Max
-492.02 -85.38 -9.89 82.85 407.53
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 235.35384 29.77755 7.904 7.54e-14 *
Producción 0.67687 0.02962 22.853 < 2e-16 *
---
Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 128 on 262 degrees of freedom
Multiple R-squared: 0.6659, Adjusted R-squared: 0.6647
F-statistic: 522.3 on 1 and 262 DF, p-value: < 2.2e-16