Caracterización de las series de tiempo

Ruido blanco (White Noise)

Un Ruido Blanco es una serie temporal que no tiene un patrón y por lo cual no se puede predecir el futuro.

Para que la serie de tiempo sea Ruido Blanco debe tener:

Media constante.
Varianza constante.
Sin autocorrelaciones en ningún período.

El Ruido Blanco es una secuencia de datos aleatorios donde cada valor tiene un período de tiempo asociado y la serie de tiempo se tiene un comportamiento aleatorio y no se puede proyectar el futuro.

Autocorrelación

Mide la correlación de la serie con versiones anteriores de la misma.

\[\rho=corr(x_t,x_{t-1})\]

La falta de autoccorrelación significa que no hay una relación entre valores pasados y valores presentes.

import pandas as pd
import numpy as np

datos = pd.read_csv('Precio.csv', sep=';', decimal=',')

len(datos)

datos.head()

	Fecha	Precio
0	1/03/2003	72.412500
1	2/03/2003	72.837083
2	3/03/2003	70.103750
3	4/03/2003	70.770417
4	5/03/2003	69.153750

datos.tail()

	Fecha	Precio
5812	27/01/2019	240.19
5813	28/01/2019	306.09
5814	29/01/2019	296.29
5815	30/01/2019	298.31
5816	31/01/2019	309.06

Convertir la columna Fecha de los datos cargados como fechas.

datos.Fecha = pd.to_datetime(datos.Fecha, dayfirst = True)

datos.head()

	Fecha	Precio
0	2003-03-01	72.412500
1	2003-03-02	72.837083
2	2003-03-03	70.103750
3	2003-03-04	70.770417
4	2003-03-05	69.153750

Convertir las fechas como el index.

datos.set_index('Fecha', inplace=True)

datos.head()

	Precio
Fecha
2003-03-01	72.412500
2003-03-02	72.837083
2003-03-03	70.103750
2003-03-04	70.770417
2003-03-05	69.153750

Gráfica de la serie de tiempo cargada

import matplotlib.pyplot as plt

datos.plot()
plt.show()

Como las fechas se convirtieron a index, salen en el eje X del gráfico.

Ejemplo de Ruido Blanco

Se creará una serie de tiempo Ruido Blanco a partir de la media y la desviación estándar de los datos cargados

wn = np.random.normal(loc = datos.mean(), scale = datos.std(), size = len(datos))

datos['wn'] = wn #Para agregar los valores de wn en una columna.

datos.head()

	Precio	wn
Fecha
2003-03-01	72.412500	68.762652
2003-03-02	72.837083	-12.488899
2003-03-03	70.103750	150.336584
2003-03-04	70.770417	15.468834
2003-03-05	69.153750	8.528356

datos.describe()

	Precio	wn
count	5817.000000	5817.000000
mean	139.017727	139.923242
std	144.002145	142.741753
min	35.940000	-306.202509
25%	70.983333	43.546751
50%	97.480000	142.477725
75%	155.160000	236.312871
max	1952.180000	668.576254

Gráfico de la serie de tiempo Ruido Blanco

datos.wn.plot(figsize = (20,5))
plt.title("White Noise Time-Series", size= 24)
plt.show()

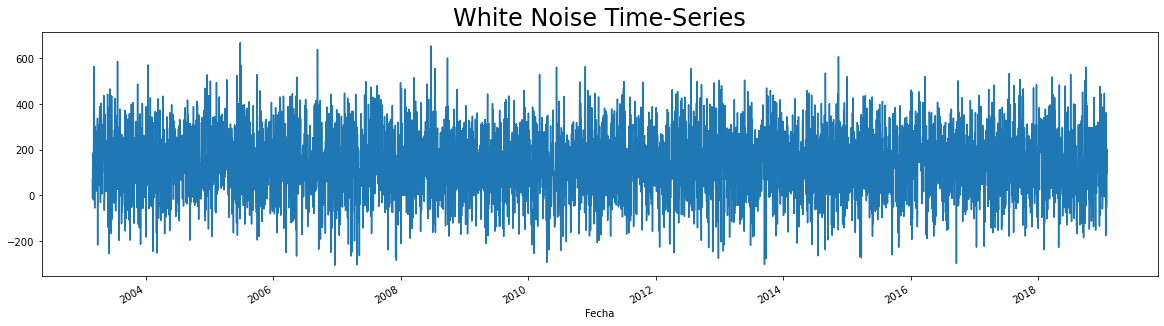
Caminata Aleatoria (Random Walk)

En la Caminata Aleatoria los valores tienen a persistir en el tiempo y las diferencias entre períodos son Ruido Blanco.

\[P_t=P_{t-1}+\epsilon_t\]

\(\epsilon_t:\) es un residuo aleatorio Ruido Blanco.

La mejor estimación de \(P_t\) es \(P_{t-1}\). Los patrones pasados persistirán en el futuro. Así, la mejor estimación del precio de mañana será el precio de hoy.

\[\epsilon_t\sim WN(\mu,\sigma^2)\]

Ejemplo de Caminata Aleatoria

rw = pd.read_csv('RandWalk.csv', sep=',', decimal='.')

rw.head()

	date	price
0	07/01/1994	1122.139662
1	08/01/1994	1135.238562
2	09/01/1994	1109.897831
3	10/01/1994	1080.347860
4	11/01/1994	1082.095245

rw.date = pd.to_datetime(rw.date, dayfirst = True)
rw.set_index('date', inplace=True)

rw.head()

	price
date
1994-01-07	1122.139662
1994-01-08	1135.238562
1994-01-09	1109.897831
1994-01-10	1080.347860
1994-01-11	1082.095245

rw.plot(figsize = (20,5))
plt.title("Random Walk", size= 24)
plt.show()

Generación de Caminata Aleatoria

# Generamos 500 pasos aleatorios para la caminara, con media 0 y desviación estándar 1
steps = np.random.normal(loc=0, scale=1, size=500)

# Ponemos el primer elemento a 0 para que el precio inicial sea el que pongamos nosotros
steps[0]=0

# Simulando los precios P con un precio inicial de 100
P = 100 + np.cumsum(steps)

plt.plot(P)
plt.title("Random Walk Simulada")
plt.show()

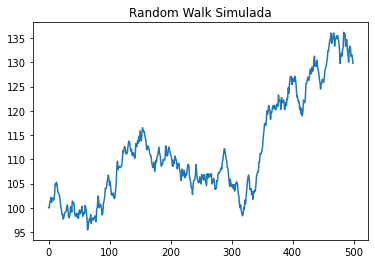
Esta gráfica se generará aleatoriamente, es decir, que siempre será una diferente cada vez que se corre el código.

Estacionariedad (Stationarity)

Una serie de tiempo es estacionaria cuanda la media y la varianza son constantes en el tiempo y no tiene tendencia.

Los valores de la serie de tiempo oscilan alrededor de la media constante y la variabilidad con respecto a esa media también permanece constante en el tiempo.

Por el contrario, las series no estacionarias tienen tendencia o la variabilidad cambia en el tiempo. Los cambios en la media determinan una tendecia y los valores no oscilarán alrededor de la media.

\(\mu:\) Media constante.

\(\sigma^2:\) Varianza constante.

Esto implica, que si la serie de tiempo es estacionaria:

\[cov(S_1)=cov(S_2)\]

Esto también se conoce como estacionariedad en forma débil. Entonces, la serie de tiempo tiene estacionariedad en forma débil o estacionariedad en covarianzas.

Una serie de tiempo es estacionaria en covarianza si cumple con los siguientes tres supuestos:

\(\mu:\) Media constante.
\(\sigma^2:\) Varianza constante.
Datos con covarianza constante entre períodos que estén a una distancia idéntica al otro dato (\(k\)):

\[cov(x_n,x_{n+k}) = cov(x_m,x_{m+k})\]

El Ruido Blanco es una serie de tiempo estacionaria en covarianza o débilmente estacionaria

Adicionalmente, el Ruido Blanco no presenta autocorrelaciones. Por tanto, la correlación entre dos puntos en el tiempo (\(x_n,x_{x+k}\)) es igual a cero. En consecuencia, si \(corr(x_n,x_{x+k})=0\), entonces, \(cov(x_n,x_{n+k})=0\).

\[cov(x_n,x_{n+k})=corr(x_n,x_{x+k})\sigma_n\sigma_{n+k}\]

Estacionariedad Estricta

Esto significa que las muestras aleatorias de la serie de tiempo tienen la misma distribución, es decir, distribuciones idénticas o idénticamente distribuidas (i.i.d.).

Para cualquier variable aleatoria estrictamente estacionaria:

\[(x_t,x_{t+k})\sim i.i.d(\mu,\sigma^2)\]

\[(x_{t+\tau},x_{t+k+\tau})\sim i.i.d(\mu,\sigma^2)\]

Prueba de Estacionariedad

La prueba de Dickey-Fuller (David Dickey y Wayne Fuller) permite identificar si un conjunto de datos provienen de un proceso estacionario. También se conoce como prueba D-F.

Hipótesis:

\(H_0:\) la serie no es estacionaria.

\(H_1:\) la serie es estacionaria.

\(H_0:\) \(\varphi_1=1\)

\(H_1:\) \(\varphi_1<1\)

\(\varphi_1:\) Coeficiente de autocorrelación de un retraso.

Coeficiente de autocorrelación:

Es el coeficiente de correlación entre dos valores en una serie temporal.

\[\varphi_k=corr(x_t,x_{t-k})\]

\(k:\) retraso. Intervalo de tiempo entre los dos perídos.

Coeficiente de correlación de 1 retraso:

\(k=1\)

\[\varphi_1=corr(x_t,x_{t-1})\]

Es la correlación entre dos valores separados por 1 solo período de tiempo.

Prueba de Dickey-Fuller

Se calcula un estadístico de prueba (\(\lambda_0\)), también se llama estadístico de constrate.

Este estadístico de prueba se compara con un valor crítico (\(\lambda_{crítico}\)).

Si \(\lambda_0<\lambda_{crítico}:\) se rechaza \(H_0\). Por tanto, la serie es estacionaria.

Otra forma es calculando el \(p-valor\) con el cual se obtiene la probabilidad de que aceptar la hipótesis nula \(H_0\).

Si \(p-valor\) es cercano a cero, la probabilidad de aceptar la hipótesis nula \(H_0\) es pequeña.

\(\alpha:\) nivel de significancia.

\(1-\alpha:\) nivel de confianza.

Si la confianza es del 95% \((1-\alpha=0,95)\), la significancia es del 5% \((\alpha=0,05)\)

Si \(p-valor<\alpha:\) se rechaza \(H_0\). Por tanto, la serie es estacionaria.

import statsmodels.tsa.stattools as sts

sts.adfuller(datos.Precio)

(-5.14735564904873,
 1.1249833584986309e-05,
 29,
 5787,
 {'1%': -3.4314804999155433,
  '5%': -2.8620395736712436,
  '10%': -2.5670359210987224},
 53341.43530925218)

(-5.147355649048741, ← \(\lambda_0\)

1.1249833584985765e-05, ← \(p-valor\)

29, ← Período de tiempo con el que existe autocorrelación.

5787, ← Cantidad de datos de la serie de tiempo.

\(\lambda_0=-5,147355649048741\)

Valores críticos :math:`(lambda_{crítico})` dependiendo del nivel de confianza:

{'1%': -3.4314804999155433, '5%': -2.8620395736712436, '10%': -2.5670359210987224},

Para un nivel de confianza del 95%, la serie de tiempo es estacionaria:

\[\lambda_0=-5,147355649048741<\lambda_{crítico}=-2,8620395736712436\]

La hipótesis nula, \(H_0\), se rechaza.

Otra forma:

\(p-valor=1,1249833584985765e-05\)

Para un nivel de confianza del 95%, la serie de tiempo es estacionaria:

\[p-valor=1,1249833584985765e-05<\alpha=0,05\]

La hipótesis nula, \(H_0\), se rechaza.

Sin embargo, el valor de 29 es el número de retrasos utilizado para calcular el estadístico. Esto significa que existe autocorrelación con el período 29 de la serie de tiempo.

(-5.147355649048741, 1.1249833584985765e-05, 29,← Este valor.

Lo ideal es tener el este valor menor a 1.

sts.adfuller(wn)

(-76.4332510296946,
 0.0,
 0,
 5816,
 {'1%': -3.4314748604753023,
  '5%': -2.862037082045299,
  '10%': -2.567034594734868},
 73784.13313234002)

En este caso no hay autocorrelación:

(-76.88442938788081, 0.0, 0,← No hay un período de tiempo en la serie con el que se tenga autocorrelación.

Esta serie de tiempo sí es estacionaria.

sts.adfuller(rw)

(-1.5198946901184311,
 0.5236477720694186,
 0,
 7028,
 {'1%': -3.4312808039348894,
  '5%': -2.8619513408164483,
  '10%': -2.566988952715846},
 62547.63026051087)

Esta serie de tiempo no es estacionaria a pesar de no presentar autocorrelación.

\[\lambda_0=-1,5198946901184334>\lambda_{crítico}=-2,8619513408164483\]

\[p-valor=0,5236477720694175>\alpha=0,05\]

\(H_0\) se acepta.

Esta conclusión también se llega con los otros niveles de confianza.

Estacionalidad (Seasonality)

Se observan tendencias que aparecen de forma cíclica. Ejemplo: las estaciones del clima.

Son tendencias repetitivas.

Para identificar existencia de estacionalidad la serie de tiempo se puede descomponer en lo siguiente:

Tendencia: patrón. \(\mu\)
Estacional: ciclos. \(S\)
Residual: error. \(\epsilon\)

Descomposición clásica:

Se espera relación lineal entre las tres partes de la serie de tiempo.

Puede ser una descomposición aditiva o multiplicativa.

1. Aditiva:

\[X_t=\mu_t+S_t+\epsilon_t\]

2. Multiplicativa:

\[X_t=\mu_t \times S_t \times \epsilon_t\]

from statsmodels.tsa.seasonal import seasonal_decompose

Aditiva:

s_dec_additive = seasonal_decompose(rw, model = "additive")
s_dec_additive.plot()
plt.show()

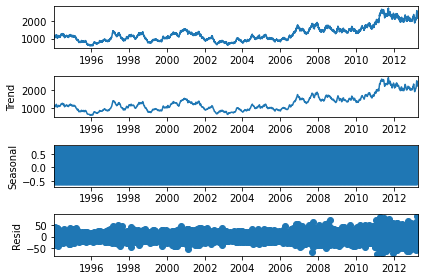
El primer gráfico es la serie de tiempo origial, sin descomponer.

El segundo gráfico es la tendencia, si es similar al primero, la serie de tiempo no es estacional.

Si el gráfico de la estacionalidad, tercer gráfico, se parece a un rectángulo, es porque los valores están oscilando de un lado a otro y el gráfico es muy pequeño para identificar esos cambios. Esto significa que, para cada período no existe un patrón cíclico completo. Con esto se sugiere que no hay estacionalidad.

Multiplicativa:

s_dec_multiplicative = seasonal_decompose(rw, model = "multiplicative")
s_dec_multiplicative.plot()
plt.show()

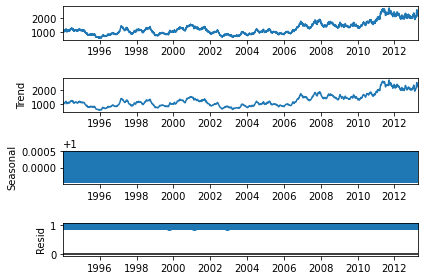
Misma conclusión, no hay estacionalidad.

Autocorrelación

\[corr(x_t,x_{t-k})\]

Función de autocorrelación - ACF (Autocorrelation Funtion):

Calcula la autocorrelación para cualquier retraso \((k)\).

ACF

import statsmodels.graphics.tsaplots as sgt

sgt.plot_acf(datos.Precio, lags = 40, zero = False)
plt.title("ACF", size = 24)
plt.show()

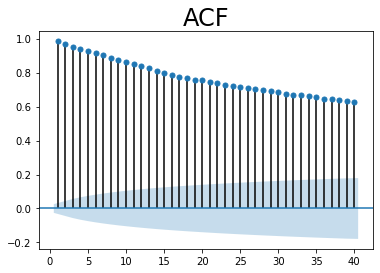
lags = 40: retrasos. En este caso, los 40 períodos antes del período actual.

zero = False: para no incluir el período actual. No es necesario mostrar la autocorrelación entre cada valor y sí mismo poque es 1.

El área sombreada en el gráfico representa la signifación de los valores de la autocorrelación indicando si son significativamente distintos de cero. Como cada valor de autocorrelación está por encima del área sombreada, esto indica que los coeficientes de autocorrelación son significativos.

Conclusión: la serie de tiempo está autocorrelacionada.

sgt.plot_acf(wn, lags = 40, zero = False)
plt.title("ACF del Ruido Blanco", size = 24)
plt.show()

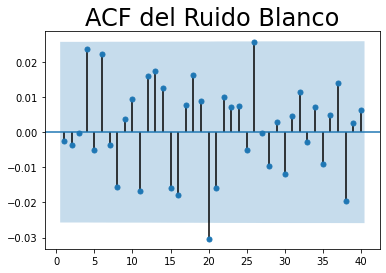
La mayoría de los coeficientes de autocorrelación no son significativos porque están dentro del área sombreada. Esto indica que no hay autocorrelación para ningún retraso. Esto es uno de los supuestos del Ruido Blanco.

Conclusión: la serie de tiempo no está autocorrelacionada.

sgt.plot_acf(rw, lags = 40, zero = False)
plt.title("ACF de la Caminata Aleatoria", size = 24)
plt.show()

Función de autocorrelación parcial - PACF (Partial Autocorrelation Funtion):

Se determina el efecto que tiene el valor del período \(t-k\) sobre el período \(t\). No determina los efectos entre los períodos intermedios.

Conclusión: la serie de tiempo está autocorrelacionada.

PACF

sgt.plot_pacf(datos.Precio, lags = 40, zero = False, method = ('ols'))
plt.title("PACF", size = 24)
plt.show()

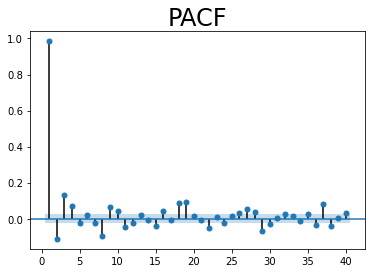
method = ('ols'): método para determinar el PACF. Método de mínimos cuadrados ordinarios (OLS-Ordinary Least Squares).

Conclusión: la serie de tiempo está autocorrelacionada.

sgt.plot_pacf(wn, lags = 40, zero = False, method = ('ols'))
plt.title("PACF para Ruido Blanco", size = 24)
plt.show()

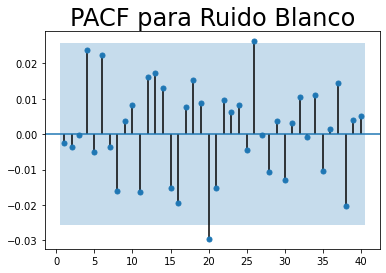
Conclusión: la serie de tiempo no está autocorrelacionada.

sgt.plot_pacf(rw, lags = 40, zero = False, method = ('ols'))
plt.title("PACF para la Caminata Aleatoria", size = 24)
plt.show()

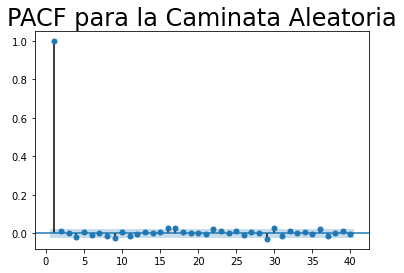
Conclusión: la serie de tiempo no está autocorrelacionada.