Regresión Lineal Múltiple (RLM)

En la regresión lineal múltiple tenemos más de una variable regresora o independiente. Este modelo se representa por la siguiente fórmula:

\[y = \beta_0+\beta_1 x_1 +\beta_2 x_2 + ... + \beta_k x_x +\varepsilon\]

Donde,

\(y\): variable dependiente o variable respuesta.

\(x_j\): variables independientes o regresoras. También llamadas variables explicativas.

\(\beta_j\): coeficientes de regresión.

\(k\): cantidad de variables regresoras o explicativas.

\(\varepsilon\): error

El modelo de regresión lineal múltiple con \(k\) regresores es un hiperplano en el espacio \(k\) dimensiones. El parámetro \(\beta_j\) representa el cambio esperado en la variable \(y\) por un cambio unitario de \(x_j\) cuando las demás variables explicativas \(x_i\) \((i \neq i\) se mantienen constantes. Por esta razón, los \(\beta_j\) se pueden llamar coeficientes de regresión parcial.

Este modelo es lineal porque la ecuación es una función lineal de los parámetros desconocidos \(\beta_j\).

Los parámetros se pueden estimar a partir de datos muestrales. La siguiente tabla muestra la forma de los datos para \(n\) observaciones, \(k\) variables independientes y una &y& variable dependiente.

En este modelo se supone que \(n>k\), \(E(\varepsilon) = 0\), \(Var(\varepsilon)= \sigma^2\) y que los errores no están correlacionados.

Tabla

Con los datos muestrales, el modelo se puede expresar de la siguiente forma:

\[y_i = \beta_0 + \sum_{j=1}^k {\beta_j x_{ij}} + \varepsilon_i\]

Mínimo cuadrados:

El método de mínimos cuadrado se aplica para estimar los coeficientes de regresión \((\beta_j)\). La función de mínimos cuadrados es:

\[S(\beta_0,\beta_1,...,\beta_k)=\sum_{i=i}^n{\varepsilon_i^2}\]

\[S(\beta_0,\beta_1,...,\beta_k)=\sum_{i=1}^n{(y_i-\beta_0-\sum_{j=1}^k {\beta_j x_{ij}})^2}\]

El objetivo es minimizar la función \(S\) respecto a los Betas.

El modelo de regresión lineal múltiple se puede expresar en forma matricial:

\[y = X\beta+\varepsilon\]

Donde,

\(y = \begin{bmatrix} y_1 \\ y_2 \\ . \\ y_n \end{bmatrix}, X = \begin{bmatrix} 1 & x_{11} & x_{12} & ... & x_{1k} \\ 1 & x_{21} & x_{22} & ... & x_{2k} \\ . & . & . & ... & . \\ 1 & x_{n1} & x_{n2} & ... & x_{nk} \end{bmatrix}\)

\(\beta=\begin{bmatrix} \beta_0 \\ \beta_1 \\ . \\ \beta_k \end{bmatrix}, \varepsilon = \begin{bmatrix} \varepsilon_1 \\ \varepsilon_1 \\ . \\ \varepsilon_n \end{bmatrix}\)

\(y\) es un vector de \(n\times 1\).

\(X\) es una matriz de \(n\times p\). \(p\) cantidad de variables regresoras.

\(\beta\) es un vector de \(p\times 1\).

\(\varepsilon\) es un vector de \(n\times 1\).

Estimación de los Betas:

Con el método de mínimos cuadrados se busca determinar el vector \(\hat{\beta}\) que minimice la ecuación de \(S\). En forma matricial este vector se halla así:

\[\hat{\beta} = (X^´X)^{-1}X^´y\]

Donde \(X^´\) es la transpuesta de la matriz \(X\).

Se obtiene una solución si existe la inversa de \((X^´X)^{-1}\). Esta matriz existe si las regresoras son linealmente independientes, esto es, que ninguna columna de \(X\) sea una combinación lineal de las demás columnas.

El modelo de regresión ajustado se expresa con la siguiente ecuación:

\[\hat y = x^´\hat{\beta} = \hat{\beta_0}+\sum_{j=1}^k{\hat{\beta_j}x_j}\]

El residual es la diferencia entre el valor observado, \(y_i\), y el valor ajustado \(\hat y\) así: \(\hat{\varepsilon_i} = y_i-\hat{y_i}\). Para \(n\) observaciones se tiene \(n\) residuales.

Código en R:

datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))

   Fecha PrecioInterno PrecioInternacional Producción Exportaciones     TRM
ene-00        371375              130.12        658           517 1923.57
feb-00        354297              124.72        740           642 1950.64
mar-00        360016              119.51        592           404 1956.25
abr-00        347538              112.67       1055           731 1986.77
may-00        353750              110.31       1114           615 2055.69
jun-00        341688              100.30       1092           869 2120.17
     EUR
1916.0
1878.5
1875.0
1832.0
1971.5
2053.5

dim(datos)

264
7

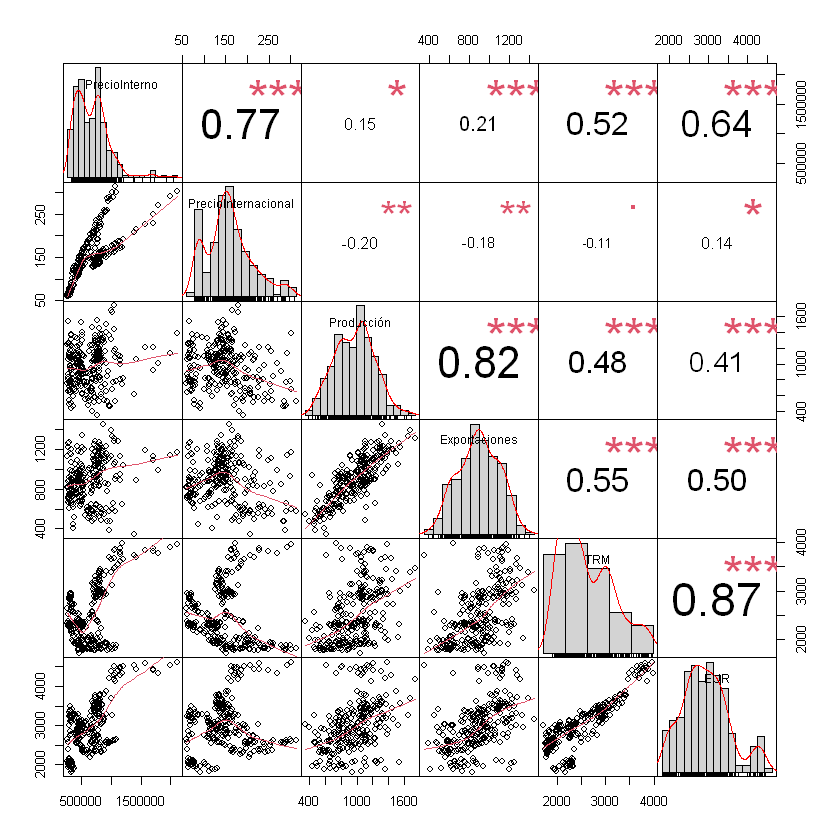
Matriz de correlaciones:

install.packages("PerformanceAnalytics")

library(PerformanceAnalytics)

Warning message:
"package 'PerformanceAnalytics' was built under R version 4.1.3"
Loading required package: xts

Warning message:
"package 'xts' was built under R version 4.1.3"
Loading required package: zoo

Warning message:
"package 'zoo' was built under R version 4.1.3"

Attaching package: 'zoo'

The following objects are masked from 'package:base':

    as.Date, as.Date.numeric

Attaching package: 'PerformanceAnalytics'

The following object is masked from 'package:graphics':

    legend

chart.Correlation(datos[,2:7])

Ajuste del modelo 1:

\[y = \beta_0+\beta_1 x_1 +\beta_2 x_2 + +\beta_3 x_3 + +\beta_4 x_4 + +\beta_5 x_5 +\varepsilon\]

\[Exportaciones = \beta_0+\beta_1Producción +\beta_2 PrecioInternacional +\beta_3 PrecioInterno ++\beta_4TRM +\beta_5 EUR +\varepsilon\]

regression <- lm(Exportaciones ~ Producción + PrecioInternacional + PrecioInterno + TRM + EUR, data = datos)
regression

Call:
lm(formula = Exportaciones ~ Producción + PrecioInternacional +
    PrecioInterno + TRM + EUR, data = datos)

Coefficients:
        (Intercept)           Producción  PrecioInternacional
          2.800e+02            5.806e-01           -1.045e+00
      PrecioInterno                  TRM                  EUR
          1.878e-04           -3.049e-02            5.335e-02

summary(regression)

Call:
lm(formula = Exportaciones ~ Producción + PrecioInternacional +
    PrecioInterno + TRM + EUR, data = datos)

Residuals:
    Min      1Q  Median      3Q     Max
-507.57  -73.29   -2.66   74.68  400.44

Coefficients:
                      Estimate Std. Error t value Pr(>|t|)
(Intercept)          2.800e+02  1.172e+02   2.390   0.0176 *
Producción           5.806e-01  3.284e-02  17.681   <2e-16 *
PrecioInternacional -1.045e+00  6.248e-01  -1.673   0.0956 .
PrecioInterno        1.878e-04  1.311e-04   1.432   0.1533
TRM                 -3.049e-02  5.367e-02  -0.568   0.5704
EUR                  5.335e-02  2.725e-02   1.958   0.0513 .
---
Signif. codes:  0 '*' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 121.1 on 258 degrees of freedom
Multiple R-squared:  0.7055,        Adjusted R-squared:  0.6998
F-statistic: 123.6 on 5 and 258 DF,  p-value: < 2.2e-16

Coeficientes:

print(regression$coefficients)

  (Intercept)          Producción PrecioInternacional       PrecioInterno
 2.800080e+02        5.806015e-01       -1.045120e+00        1.877758e-04
          TRM                 EUR
-3.049381e-02        5.335477e-02

Residuales:

print(head(regression$residuals))

         1          2          3          4          5          6
-122.35878  -44.57864 -202.81077 -146.20990 -305.43969  -49.27200

print(length(regression$residuals))

[1] 264

Ajuste del modelo 2:

\[Exportaciones = \beta_0+\beta_1Producción +\beta_2 PrecioInternacional +\beta_3 EUR +\varepsilon\]

regression <- lm(Exportaciones ~ Producción + PrecioInternacional + EUR, data = datos)
summary(regression)

Call:
lm(formula = Exportaciones ~ Producción + PrecioInternacional +
    EUR, data = datos)

Residuals:
    Min      1Q  Median      3Q     Max
-508.69  -75.56    1.87   72.06  423.92

Coefficients:
                     Estimate Std. Error t value Pr(>|t|)
(Intercept)         133.89907   43.16546   3.102  0.00213 **
Producción            0.59395    0.03210  18.502  < 2e-16 *
PrecioInternacional  -0.25609    0.13838  -1.851  0.06535 .
EUR                   0.07345    0.01321   5.560 6.69e-08 *
---
Signif. codes:  0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 121.4 on 260 degrees of freedom
Multiple R-squared:  0.7017,        Adjusted R-squared:  0.6982
F-statistic: 203.8 on 3 and 260 DF,  p-value: < 2.2e-16

Ajuste del modelo 3:

\[Exportaciones = \beta_0+\beta_1Producción +\beta_2 EUR +\varepsilon\]

regression <- lm(Exportaciones ~ Producción + EUR, data = datos)
summary(regression)

Call:
lm(formula = Exportaciones ~ Producción + EUR, data = datos)

Residuals:
    Min      1Q  Median      3Q     Max
-512.46  -81.73   -2.56   78.98  441.24

Coefficients:
            Estimate Std. Error t value Pr(>|t|)
(Intercept) 97.73831   38.66817   2.528   0.0121 *
Producción   0.61093    0.03091  19.767  < 2e-16 *
EUR          0.06732    0.01285   5.240 3.32e-07 *
---
Signif. codes:  0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 122 on 261 degrees of freedom
Multiple R-squared:  0.6977,        Adjusted R-squared:  0.6954
F-statistic: 301.2 on 2 and 261 DF,  p-value: < 2.2e-16