Regresión Lineal Simple (RLS)
1. Modelación: Desarrollar un modelo de regresión.
2. Estimación: Usar R para estimar el modelo.
3. Inferencia: Interpretar el modelo de regresión estimado.
4. Predicción: Realizar predicciones sobre la variable de interés.
Con la regresión lineal se busca modelar la relación entre una o múltiples variables independientes (\(X_i\)) y una variable dependiente (\(y\)). También se puede predecir resultados en una escala continua.
De forma univariada se modela la relación entre una característica simple (una sola variable explicativa \(X\)) y una respuesta de valor continua (variable dependiente \(y\)). La relación lineal se define con la siguiente ecuación:
\(y\): variable dependiente o de respuesta. También llamada variable regresora.
\(X\): variable independiente.
Esta es la ecuación de una línea recta de la forma pendiente-intercepto. La variable aleatoria \(y\) es una función lineal de \(X\) con términos independientes \(\beta_0\) y pendiente \(\beta_1\). Estos dos parámetros son los que se deben estimar en la regresión lineal para describir la relación entre las variables \(X\) y \(y\). Dicho de otra forma, con la regresión lineal se busca la recta de mejor ajuste por medio de la búsqueda de los pesos óptimos (\(\beta_0\) y \(\beta_1\)).
Las regresiones lineales hacen parte del aprendizaje automático supervisado.
Las estimaciones de los pesos óptimos de \(\beta_0\) y \(\beta_1\) se realizan a partir de la muestra \((X_i, y_i)_{i=1,2,...n}\).
Los pesos estimados son \(\hat{\beta_0}\) y \(\hat{\beta_1}\) y la ecuación de la recta estimada es:
Con esta ecuación, con un valor dado de \(X_i\) se estima el valor de \(\hat{y_i}\) de la variable \(y\).
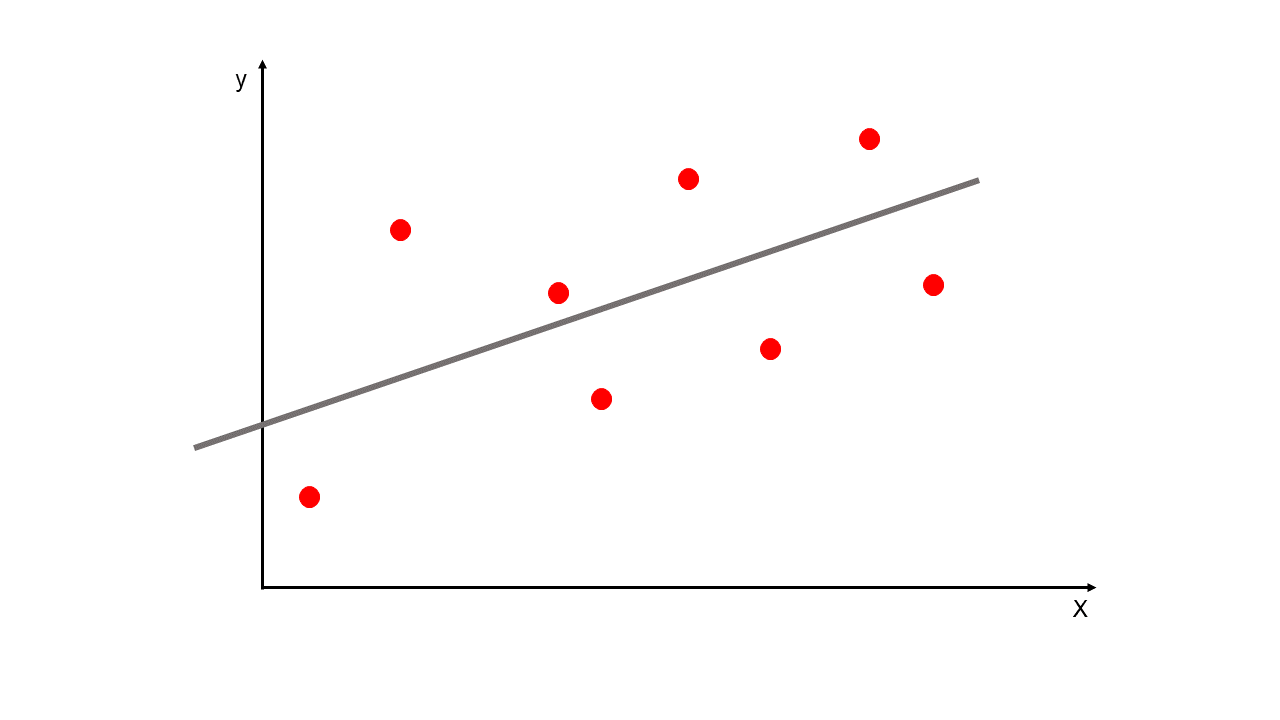
Regresión
Mínimos Cuadrados Ordinarios:
Para ajustar el método de Regresión Lineal se usa el método de Mínimos Cuadrados Ordinarios (MCO) o en inglés Ordinary Least Squares (OLS). Con esta técnica se busca encontrar la línea recta que minimiza la suma de las distancias verticales cuadradas (residuos o errores) en los puntos de la muestra. De esta forma se hallan los parámetros \(\beta_0\) y \(\beta_1\).
\(SSE\): es la suma de los errores al cuadrado (mínimas distancias verticales al cuadrado). En inglés Sum of Squared Errors. Estas distancias que son los errores se muestran en la siguiente Figura.
Como el error es: \(\hat{\varepsilon_i} = y_i-\hat{y_i}\), entonces:
Si \(SSE = 0\), entonces todos los puntos de la muestra están sobre la línea de ajuste.
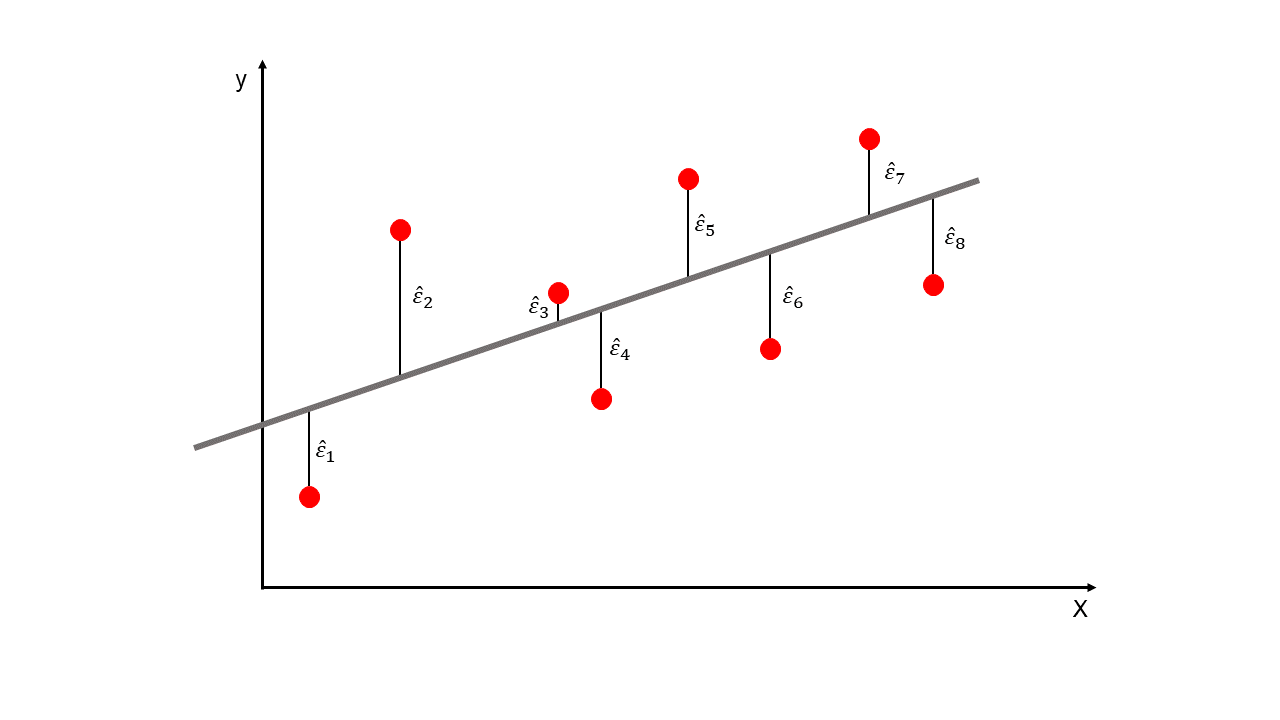
Errores
Lo que se busca es hallar los \(\beta_0\) y \(\beta_1\) que minimicen el \(SSE\), esto se hace derivando \(SSE\) con respecto a \(\beta_0\) y \(\beta_1\) y luego igualando a cero. El resultado es el siguiente:
También se puede expresar como:
Donde,
\(\overline{X}\): media de la \(X\).
\(\overline{y}\): media de la \(y\).
\(\hat{\beta_1}\) es la pendiente de la línea recta. Luego, se halla el intercepto \(\hat{\beta_0}\):
Nota: no necesitamos usar estas fórmulas para estimar los parámetros de la Regresión Lineal Simple porque tenemos códigos que lo hacen
Código en R:
datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))
Fecha PrecioInterno PrecioInternacional Producción Exportaciones TRM
1 ene-00 371375 130.12 658 517 1923.57
2 feb-00 354297 124.72 740 642 1950.64
3 mar-00 360016 119.51 592 404 1956.25
4 abr-00 347538 112.67 1055 731 1986.77
5 may-00 353750 110.31 1114 615 2055.69
6 jun-00 341688 100.30 1092 869 2120.17
EUR
1 1916.0
2 1878.5
3 1875.0
4 1832.0
5 1971.5
6 2053.5
Unidades de las variables:
Precio Interno: COP/125Kg.
PrecioInternacional: ¢USD/lb.
Producción: Miles de sacos de 60 Kg de café verde.
Exportaciones: Miles de sacos de 60 Kg de café verde.
TRM: USDCOP.
EUR: EURCOP.
Análisis exploratorio:
library(fBasics)
Loading required package: timeDate
Loading required package: timeSeries
print(basicStats(datos[,2:5]))
PrecioInterno PrecioInternacional Producción Exportaciones
nobs 2.640000e+02 264.000000 264.000000 264.000000
NAs 0.000000e+00 0.000000 0.000000 0.000000
Minimum 2.601850e+05 58.920000 345.000000 345.000000
Maximum 2.116484e+06 314.260000 1743.000000 1449.960000
1. Quartile 4.169284e+05 112.405000 775.500000 735.630000
3. Quartile 7.965564e+05 176.352500 1136.250000 1059.245000
Mean 6.426094e+05 148.611250 969.553030 891.613106
Median 6.273718e+05 143.415000 992.000000 893.290000
Sum 1.696489e+08 39233.370000 255962.000000 235385.860000
SE Mean 1.875037e+04 3.511034 16.400809 13.603671
LCL Mean 6.056894e+05 141.697937 937.259428 864.827138
UCL Mean 6.795293e+05 155.524563 1001.846633 918.399074
Variance 9.281617e+10 3254.422053 71012.445846 48855.803340
Stdev 3.046575e+05 57.047542 266.481605 221.033489
Skewness 1.478976e+00 0.622361 0.083746 -0.069626
Kurtosis 3.823024e+00 0.159010 -0.381387 -0.656356
Correlación entre variables:
La función más básica es cor(datos)
correlacion <- cor(datos[,2:5])
print(correlacion)
PrecioInterno PrecioInternacional Producción Exportaciones
PrecioInterno 1.0000000 0.7702993 0.1474286 0.2105824
PrecioInternacional 0.7702993 1.0000000 -0.2000946 -0.1789351
Producción 0.1474286 -0.2000946 1.0000000 0.8160430
Exportaciones 0.2105824 -0.1789351 0.8160430 1.0000000
print(round(correlacion, 2)) # Aproximar a dos dígitos
PrecioInterno PrecioInternacional Producción Exportaciones
PrecioInterno 1.00 0.77 0.15 0.21
PrecioInternacional 0.77 1.00 -0.20 -0.18
Producción 0.15 -0.20 1.00 0.82
Exportaciones 0.21 -0.18 0.82 1.00
Instalar la siguiente librería para graficar una matríz de correlación:
install.packages("PerformanceAnalytics")
library(PerformanceAnalytics)
Loading required package: xts
Loading required package: zoo
Attaching package: 'zoo'
The following object is masked from 'package:timeSeries':
time<-
The following objects are masked from 'package:base':
as.Date, as.Date.numeric
Attaching package: 'PerformanceAnalytics'
The following objects are masked from 'package:timeDate':
kurtosis, skewness
The following object is masked from 'package:graphics':
legend
chart.Correlation(datos[,2:7])
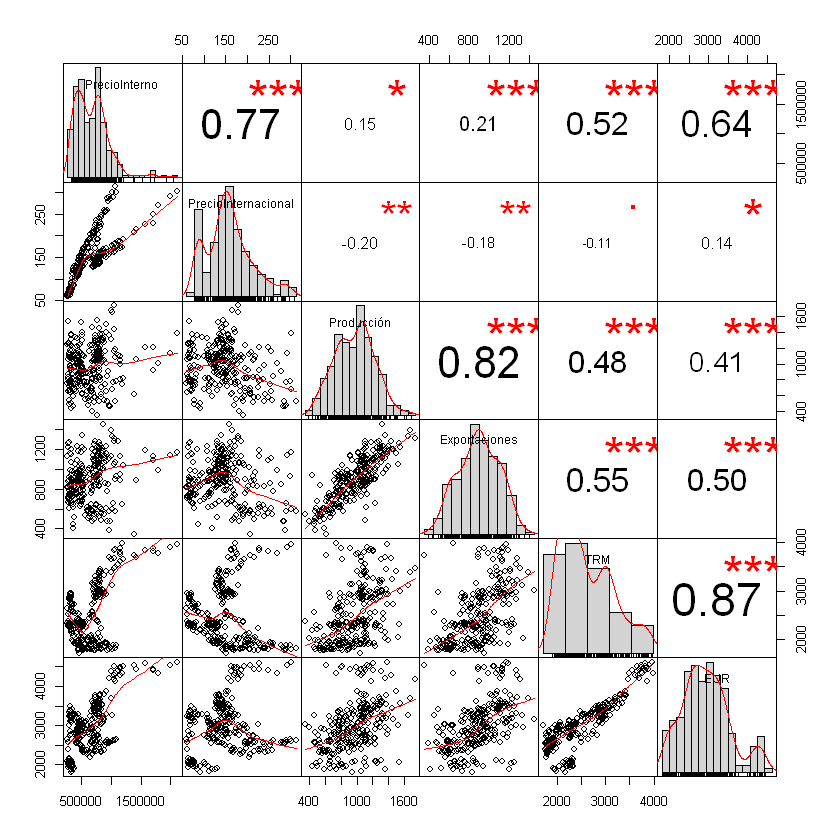
1. Modelación:
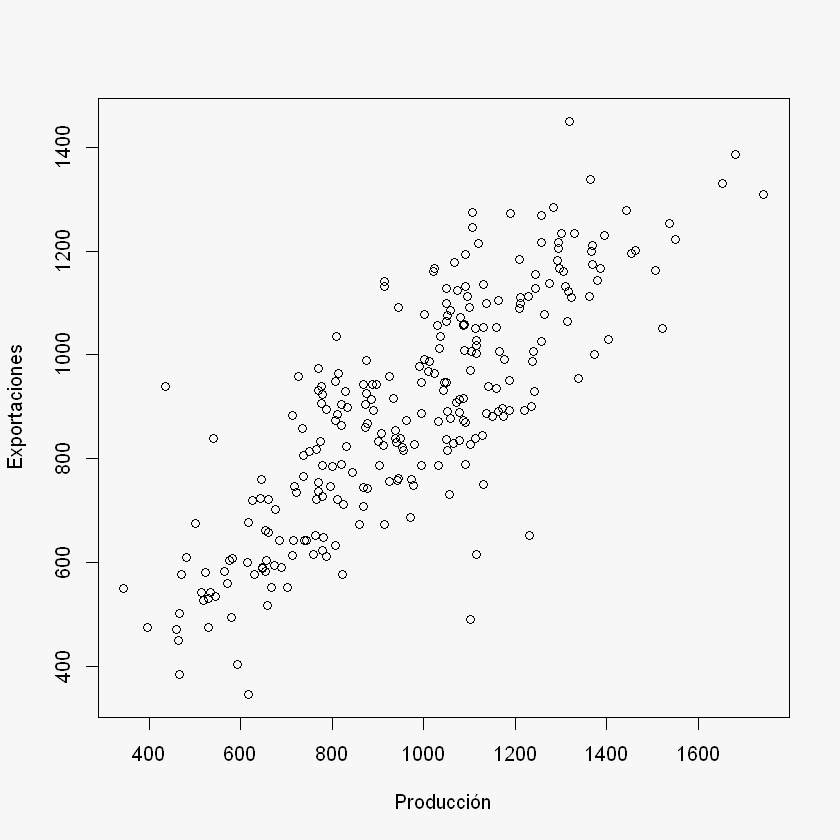
Se buscará la relación entre las Exportaciones y la Producción de la forma que las Exportaciones, \(y\), dependen de la Producción, \(y\).
X = datos$Producción
y = datos$Exportaciones
par(bg = "#f7f7f7") # Fondo gris para el gráfico
plot(X, y,
xlab = "Producción",
ylab = "Exportaciones")
2. Estimación:
Ajuste modelo de Regresión Lineal Simple:
En R se utiliza la función lm(y ~ X)
regression <- lm(y ~ X)
regression
Call:
lm(formula = y ~ X)
Coefficients:
(Intercept) X
235.3538 0.6769
Otra forma para usar lm():
lm(formula = nombre_columna_y ~ nombre_columna_X, data = datos)
regression <- lm(formula = Exportaciones ~ Producción, data = datos)
summary(regression)
Call:
lm(formula = y ~ X)
Residuals:
Min 1Q Median 3Q Max
-492.02 -85.38 -9.89 82.85 407.53
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 235.35384 29.77755 7.904 7.54e-14 *
X 0.67687 0.02962 22.853 < 2e-16 *
---
Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 128 on 262 degrees of freedom
Multiple R-squared: 0.6659, Adjusted R-squared: 0.6647
F-statistic: 522.3 on 1 and 262 DF, p-value: < 2.2e-16
cov(X, y)/var(X)
mean(y) - cov(X, y)/var(X) * mean(X)
3. Interpretación:
\(\hat{\beta_0} = 235,3538\)
\(\hat{\beta_1} = 0.6769\)
Interpretación: Cuando la variable \(X\) incrementa en una unidad, la variable \(y\) incrementa (disminuye) \(\hat{\beta_1}\) unidades.
Cuando la producción aumenta en 100 unidades, las exportaciones incrementan 67,69.
Los valores que se pueden extraer del modelo de regresión son los siguientes:
print(names(regression))
[1] "coefficients" "residuals" "effects" "rank"
[5] "fitted.values" "assign" "qr" "df.residual"
[9] "xlevels" "call" "terms" "model"
Los valores que se pueden extraer del summary del modelo de
regresión son los siguientes:
print(names(summary(regression)))
[1] "call" "terms" "residuals" "coefficients"
[5] "aliased" "sigma" "df" "r.squared"
[9] "adj.r.squared" "fstatistic" "cov.unscaled"
También se puede extraer un Data Frame con los resultados del
summary con $coef:
print(summary(regression)$coef)
Estimate Std. Error t value Pr(>|t|)
(Intercept) 235.3538372 29.77755312 7.903733 7.538088e-14
X 0.6768678 0.02961839 22.852960 2.530485e-64
Los parámetros del objeto regression se extraen con
$coefficients
Para extraer los valores de cualquier objeto puede ver en la ayuda de
las librería de la siguiente manera ?nombre librería ver los
Values
regression$coefficients # Los dos Betas
- (Intercept)
- 235.353837174437
- X
- 0.676867843609397
regression$coefficients[1] # Beta cero (intercepto)
\(\hat{\beta_0}\):
beta_0 = as.numeric(regression$coefficients[1]) # Beta cero (intercepto)
beta_0
\(\hat{\beta_1}\):
beta_1 = as.numeric(regression$coefficients[2]) # Beta 1 (pendiente)
beta_1
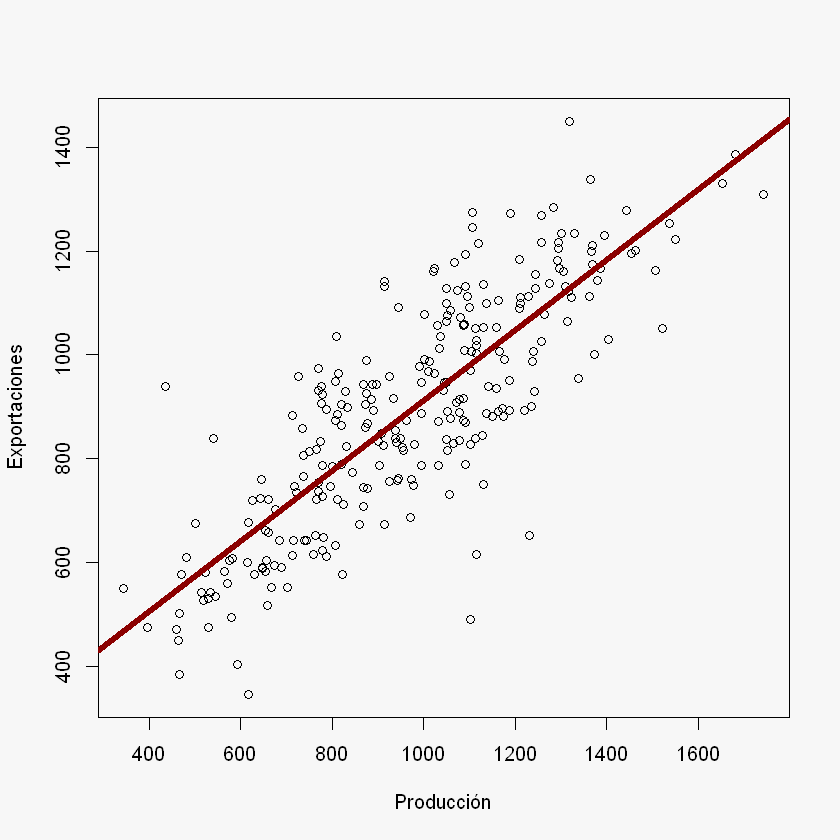
# abline - permite agregar una línea recta con solo tener intercepto - pendiente
par(bg = "#f7f7f7")
plot(X, y,
xlab = "Producción",
ylab = "Exportaciones")
abline(beta_0, beta_1, col = "darkred", lwd = 5)
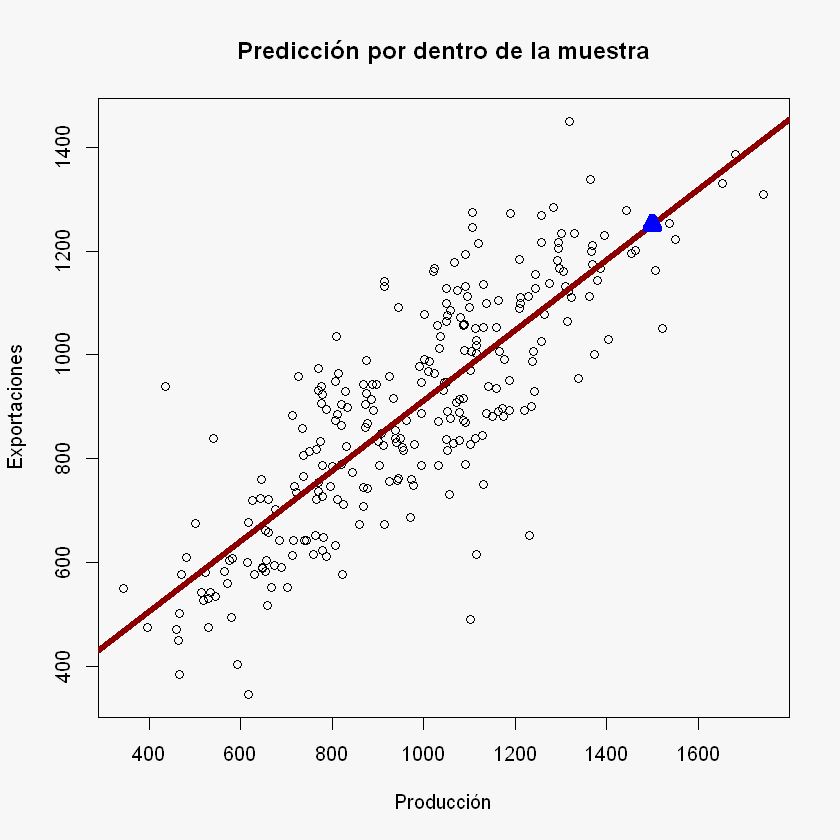
Dentro de la muestra, para una Producción de 1500, ¿cuál es la Exportación?
y_hat = beta_0 + beta_1 * 1500
y_hat
par(bg = "#f7f7f7")
plot(X, y,
xlab = "Producción",
ylab = "Exportaciones",
main = "Predicción por dentro de la muestra")
abline(beta_0, beta_1, col = "darkred", lwd = 5)
points(1500, y_hat, pch = 2, col = "blue", bg = "darkgreen", lwd = 7)
4. Predicción:
Predicción dentro de la muestra:
y_pred = beta_0 + beta_1 * X
print(head(y_pred))
[1] 680.7329 736.2360 636.0596 949.4494 989.3846 974.4935
Una forma de extraer los valores predichos o ajustados es con
$fitted.values
y_pred = regression$fitted.values
print(head(y_pred))
1 2 3 4 5 6
680.7329 736.2360 636.0596 949.4494 989.3846 974.4935
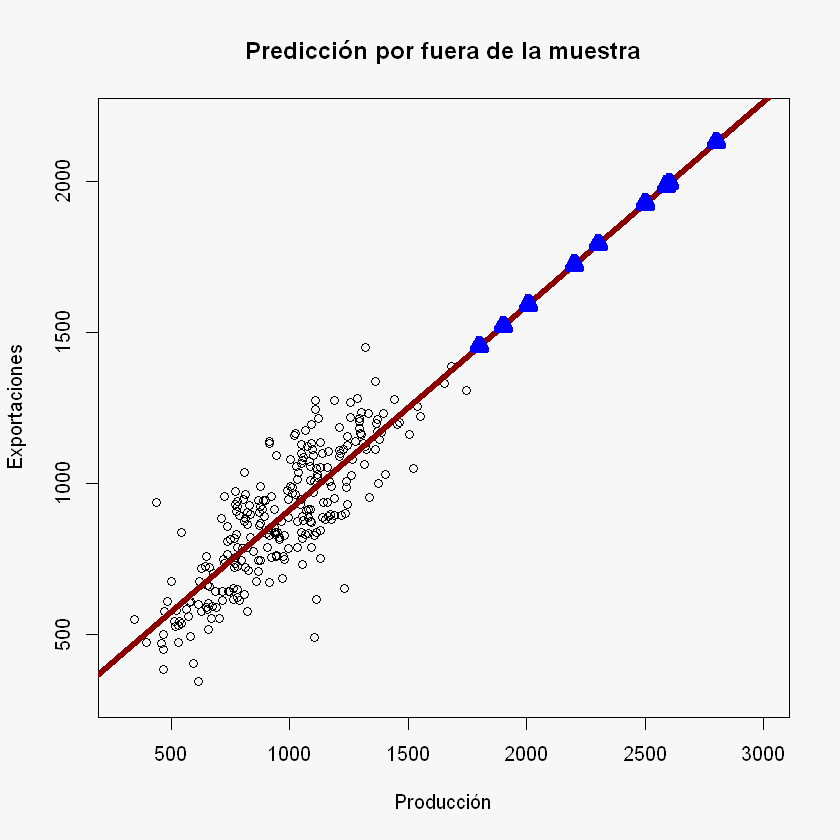
Predicción por fuera de la muestra:
nuevos_datos = c(1800.25, 1900, 2005.58, 2200.258, 2300, 2500, 2501.87, 2587, 2600, 2800) # Datos nuevo para la X (Producción)
y_pred = beta_0 + beta_1 * nuevos_datos
print(y_pred)
[1] 1453.885 1521.403 1592.866 1724.638 1792.150 1927.523 1928.789 1986.411
[9] 1995.210 2130.584
par(bg = "#f7f7f7")
plot(X, y,
xlab = "Producción",
ylab = "Exportaciones",
xlim = c(300, 3000), # Cambio de los límites para observar las predicciones por fuera de la muestra
ylim = c(300, 2200),
main = "Predicción por fuera de la muestra")
abline(beta_0, beta_1, col = "darkred", lwd = 5)
points(nuevos_datos, y_pred, pch = 2, col = "blue", bg = "darkgreen", lwd = 7)