Multicolinealidad
Este es un problema en los problemas de regresión: la multicolinealidad o dependencia casi lineal entre las variables regresoras. Este problema puede afectar la precisión con la que se estiman los coeficientes de regresión.
Con la presencia de multicolinealidad entre las variables, las varianzas de los coeficientes de regresión se inflan. Esto se mide con el VIF (Variance Inflation Factores), factores de inflación de varianzas.
Donde,
\(R^2_j\): coeficiente de determinación múltiple obtenido haciendo la regresión de \(x_j\) sobre las demás variables regresoras.
Si \(x_j\) depende casi linealmente de alguna de las demás regresoras, entonces \(R^2_j\) será casi 1, y VIF será grande. En otras palabras, si al hacer la regresión lineal múltiple donde \(x_j\) es la variable dependiente con las demás variables regresoras, y el modelo tiene buen ajuste, con alto \(R^2\), indica que \(x_j\) es linealmente dependiente de las demás variables.
Valores de VIF mayores que 10 indican problemas graves de multicolinealidad.
Si no hay relación lineal entre las variables regresoras, entonces son ortogonales. En la mayoría de los casos tendremos variables que no son ortogonales, esto no es grave, solo que se busca que no existe una relación lineal casi perfecta entre las variables independientes porque cuando hay dependencias casi lineales, se dice que existe el problema de multicolinealidad.
Se puede empezar el análisis con la matriz de correlaciones y determinar las variables que son casi linealmente dependientes cuando el coeficiente de correlación es cercano a la unidad.
Problemas de la multicolinealidad:
Covarianzas y varianzas altas de los coeficientes.
Coeficientes estimados altos en valor absoluto.
Diferentes estimaciones para diferentes muestras.
Signos de los coeficientes estimados diferentes a los estimados o con magnitudes incoherentes.
Manejo de la multicolinealidad:
Recolección de datos adicionales.
Reespecificación del modelo: se puede redefinir las variables que son casi linealmente dependientes como crear una variable regresora con la multiplicación entre ellas. También se puede eliminar alguna de estas variables, pero es posible que la variable a excluir sea muy importante para el modelo.
Código en R:
datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))
Fecha PrecioInterno PrecioInternacional Producción Exportaciones TRM
1 ene-00 371375 130.12 658 517 1923.57
2 feb-00 354297 124.72 740 642 1950.64
3 mar-00 360016 119.51 592 404 1956.25
4 abr-00 347538 112.67 1055 731 1986.77
5 may-00 353750 110.31 1114 615 2055.69
6 jun-00 341688 100.30 1092 869 2120.17
EUR
1 1916.0
2 1878.5
3 1875.0
4 1832.0
5 1971.5
6 2053.5
Matriz de coeficientes de correlación solo con las variables regresoras.
correlacion <- cor(datos[,c("PrecioInterno", "PrecioInternacional", "Producción", "TRM", "EUR")])
print(correlacion)
PrecioInterno PrecioInternacional Producción TRM
PrecioInterno 1.0000000 0.7702993 0.1474286 0.5155823
PrecioInternacional 0.7702993 1.0000000 -0.2000946 -0.1149066
Producción 0.1474286 -0.2000946 1.0000000 0.4783073
TRM 0.5155823 -0.1149066 0.4783073 1.0000000
EUR 0.6364016 0.1429278 0.4071958 0.8662474
EUR
PrecioInterno 0.6364016
PrecioInternacional 0.1429278
Producción 0.4071958
TRM 0.8662474
EUR 1.0000000
library(PerformanceAnalytics)
Warning message:
"package 'PerformanceAnalytics' was built under R version 4.1.3"
Loading required package: xts
Warning message:
"package 'xts' was built under R version 4.1.3"
Loading required package: zoo
Warning message:
"package 'zoo' was built under R version 4.1.3"
Attaching package: 'zoo'
The following objects are masked from 'package:base':
as.Date, as.Date.numeric
Attaching package: 'PerformanceAnalytics'
The following object is masked from 'package:graphics':
legend
chart.Correlation(datos[,c("PrecioInterno", "PrecioInternacional", "Producción", "TRM", "EUR")])
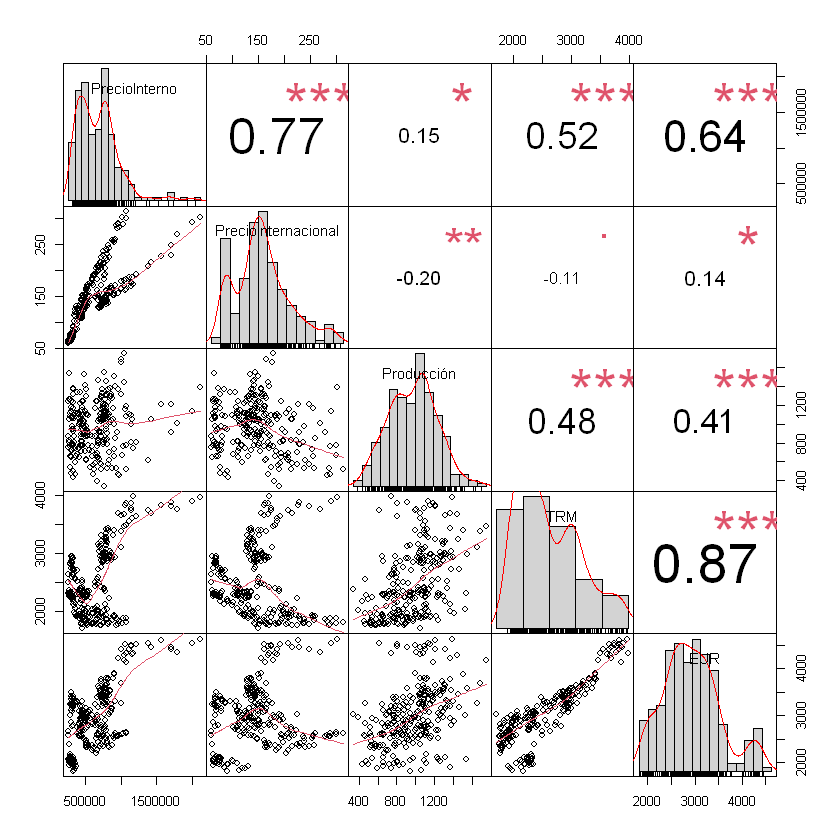
library(GGally)
Loading required package: ggplot2
Registered S3 method overwritten by 'GGally':
method from
+.gg ggplot2
ggpairs(datos[,c("PrecioInterno", "PrecioInternacional", "Producción", "TRM", "EUR")])
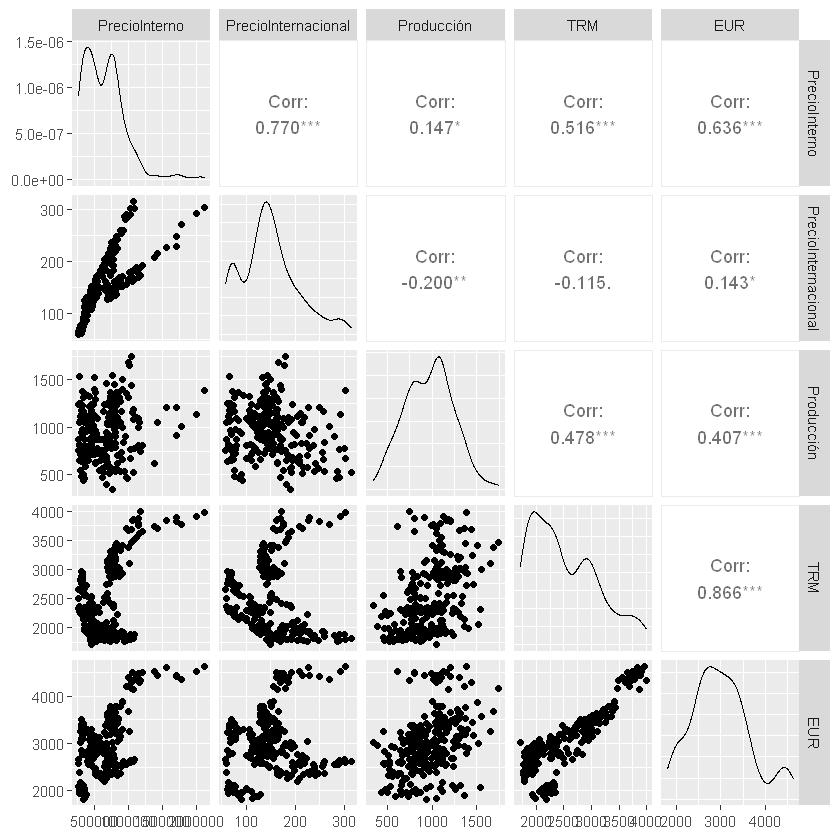
library("corrplot")
corrplot 0.92 loaded
corrplot(correlacion, method = "circle", type = "upper")
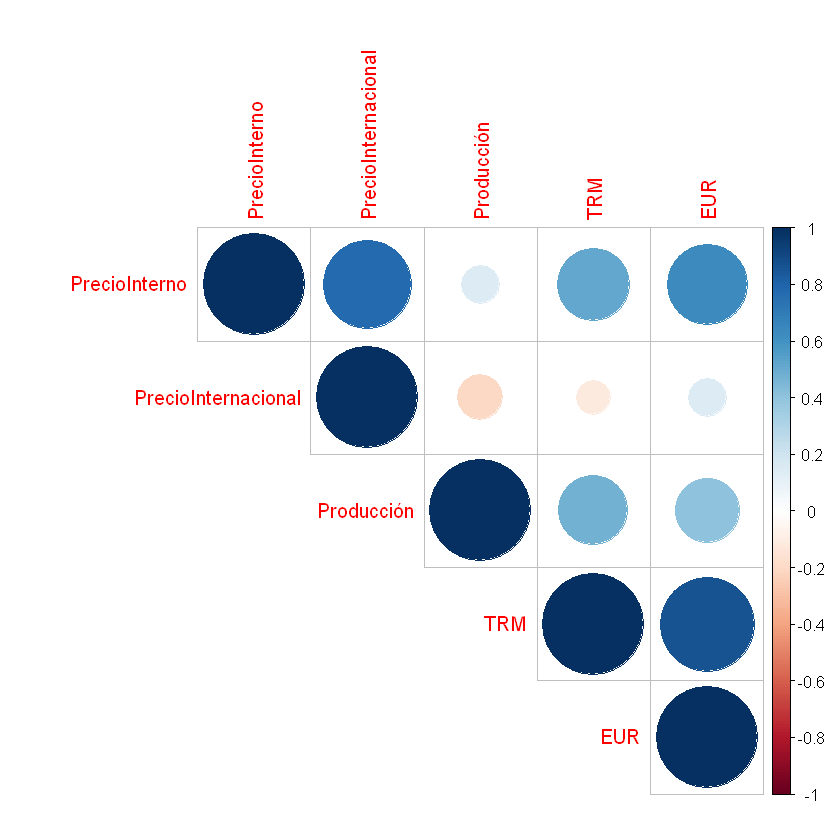
regression <- lm(Exportaciones ~ Producción + PrecioInternacional + PrecioInterno + TRM + EUR, data = datos)
summary(regression)
Call:
lm(formula = Exportaciones ~ Producción + PrecioInternacional +
PrecioInterno + TRM + EUR, data = datos)
Residuals:
Min 1Q Median 3Q Max
-507.57 -73.29 -2.66 74.68 400.44
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.800e+02 1.172e+02 2.390 0.0176 *
Producción 5.806e-01 3.284e-02 17.681 <2e-16 *
PrecioInternacional -1.045e+00 6.248e-01 -1.673 0.0956 .
PrecioInterno 1.878e-04 1.311e-04 1.432 0.1533
TRM -3.049e-02 5.367e-02 -0.568 0.5704
EUR 5.335e-02 2.725e-02 1.958 0.0513 .
---
Signif. codes: 0 '*' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 121.1 on 258 degrees of freedom
Multiple R-squared: 0.7055, Adjusted R-squared: 0.6998
F-statistic: 123.6 on 5 and 258 DF, p-value: < 2.2e-16
VIF para la variable Producción:
Se ajusta un modelo de regresión donde la variable dependiente \(y\) será Producción. Para esta prueba no se usa la variable independiente original (Exportaciones).
1/(1-summary(lm(Producción ~ PrecioInternacional + PrecioInterno + TRM + EUR, data = datos))$r.squared)
VIF para la variable Precio Internacional:
1/(1-summary(lm(PrecioInternacional ~ Producción + PrecioInterno + TRM + EUR, data = datos))$r.squared)
VIF:
Se usa la función vif() de la librería car.
library(car)
Warning message:
"package 'car' was built under R version 4.1.3"
Loading required package: carData
Warning message:
"package 'carData' was built under R version 4.1.3"
print(vif(regression))
Producción PrecioInternacional PrecioInterno TRM
1.373211 22.780668 28.609526 18.108591
EUR
5.470540
Existe el problema de multicolinealidad con las siguientes variables por tener un VIF mayor que 10:
Precio Internacional.
Precio Interno.
TRM.
Las dos variables sin el problema de multicolinealidad son:
Producción.
EUR.
Intentemos eliminar la variable Precio Internacional:
print(vif(lm(Exportaciones ~ Producción + PrecioInterno + TRM + EUR, data = datos)))
Producción PrecioInterno TRM EUR
1.322545 1.728645 4.345986 4.997328
Intentemos eliminar la variable Precio Interno:
print(vif(lm(Exportaciones ~ Producción + PrecioInternacional + TRM + EUR, data = datos)))
Producción PrecioInternacional TRM EUR
1.341211 1.376454 5.367083 5.292280
Intentemos eliminar la variable TRM:
print(vif(lm(Exportaciones ~ Producción + PrecioInternacional + PrecioInterno + EUR, data = datos)))
Producción PrecioInternacional PrecioInterno EUR
1.371007 5.467264 8.479385 3.383222
Con solo eliminar una de las variables que presentan alta multicolinealidad se soluciona este problema.