Análisis de Normalidad en RLM
Supuesto del modelo de regresión lineal:
Linealidad: el valor medio de \(y\) es una función lineal de las variables \(X\), es decir, \(y\) y \(X\) tienen una relación lineal.
Supuestos de los errores:
Independencia: los errores de la predicción, \(\varepsilon_i\), son estadisticamente independientes entre si. Los errores no están correlacionados.
Homocedasticidad (varianza constante): la varianza de los errores es constante a los largo de la distribución \(X\). Lo contrario se llama heterocedasticidad.
Normalidad: los errores son una variable aleatoria normalmente distribuida con media igual a cero. \(\varepsilon_i \sim N(0,\sigma^2)\). Esta premisa se usa para hacer pruebas de hipótesis y determinar intervalos de confianza.
Residuales escalados:
Los residuales escalados se usan para determinar observaciones atípicas o valores extremos.
Si una observación está muy separada del resto de los datos se llama atípica. Los datos influyentes son las observaciones atípicas que si se eliminan del modelo de regresión se obtienen estimaciones diferentes de los coeficientes. Una observación podría ser atípica con respecto a su valor \(y\), o a su valores de \(x\), o con respecto a todos, pero una observación atípica podría ser influyente o no serlo.
Residuales estandarizados:
Donde \(d_i\) son los residuales estandarizados. Estos tienen media cero y varianza aproximada a la unidad. \(SSE\) es la varianza aproximada de los residuales.
Con \(d_i > 3\) indica que la observación \(i\) es un dato atípico.
Residuales estudentizados:
Los residuales estudentizados son los residuales escalados con la varianza del i-ésimo residual. La varianza del i-ésimo residual es \(SSE(1- h_{ij})\). Donde \(h_{ij}\) son los elementos de la diagonal de la matriz \(H\), donde \(H=X(X^TX)^{-1}X^T\). Así que los residuales estudentizados, \(r_i\) se calculan así:
Código en R:
datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))
Fecha PrecioInterno PrecioInternacional Producción Exportaciones TRM
1 ene-00 371375 130.12 658 517 1923.57
2 feb-00 354297 124.72 740 642 1950.64
3 mar-00 360016 119.51 592 404 1956.25
4 abr-00 347538 112.67 1055 731 1986.77
5 may-00 353750 110.31 1114 615 2055.69
6 jun-00 341688 100.30 1092 869 2120.17
EUR
1 1916.0
2 1878.5
3 1875.0
4 1832.0
5 1971.5
6 2053.5
regression <- lm(Exportaciones ~ Producción + PrecioInternacional + PrecioInterno + TRM + EUR, data = datos)
regression
summary(regression)
Call:
lm(formula = Exportaciones ~ Producción + PrecioInternacional +
PrecioInterno + TRM + EUR, data = datos)
Coefficients:
(Intercept) Producción PrecioInternacional
2.800e+02 5.806e-01 -1.045e+00
PrecioInterno TRM EUR
1.878e-04 -3.049e-02 5.335e-02
Call:
lm(formula = Exportaciones ~ Producción + PrecioInternacional +
PrecioInterno + TRM + EUR, data = datos)
Residuals:
Min 1Q Median 3Q Max
-507.57 -73.29 -2.66 74.68 400.44
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.800e+02 1.172e+02 2.390 0.0176 *
Producción 5.806e-01 3.284e-02 17.681 <2e-16 *
PrecioInternacional -1.045e+00 6.248e-01 -1.673 0.0956 .
PrecioInterno 1.878e-04 1.311e-04 1.432 0.1533
TRM -3.049e-02 5.367e-02 -0.568 0.5704
EUR 5.335e-02 2.725e-02 1.958 0.0513 .
---
Signif. codes: 0 '*' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 121.1 on 258 degrees of freedom
Multiple R-squared: 0.7055, Adjusted R-squared: 0.6998
F-statistic: 123.6 on 5 and 258 DF, p-value: < 2.2e-16
Residuales:
residuales <- regression$residuals
print(head(residuales))
1 2 3 4 5 6
-122.35878 -44.57864 -202.81077 -146.20990 -305.43969 -49.27200
Residuales estandarizados:
SSE <- sum(regression$residuals^2)
residuales_stan <- regression$residuals/sqrt(SSE)
print(head(residuales_stan))
1 2 3 4 5 6
-0.06290473 -0.02291791 -0.10426516 -0.07516661 -0.15702675 -0.02533077
Residuales estudentizados:
Usamos la función de la base rstudent() para calcular los residuales
estudentizados. Se hace con el objeto del modelo ajustado.
residuales_student <- rstudent(regression)
print(head(residuales_student))
1 2 3 4 5 6
-1.0213093 -0.3716422 -1.7029943 -1.2251986 -2.5804438 -0.4105190
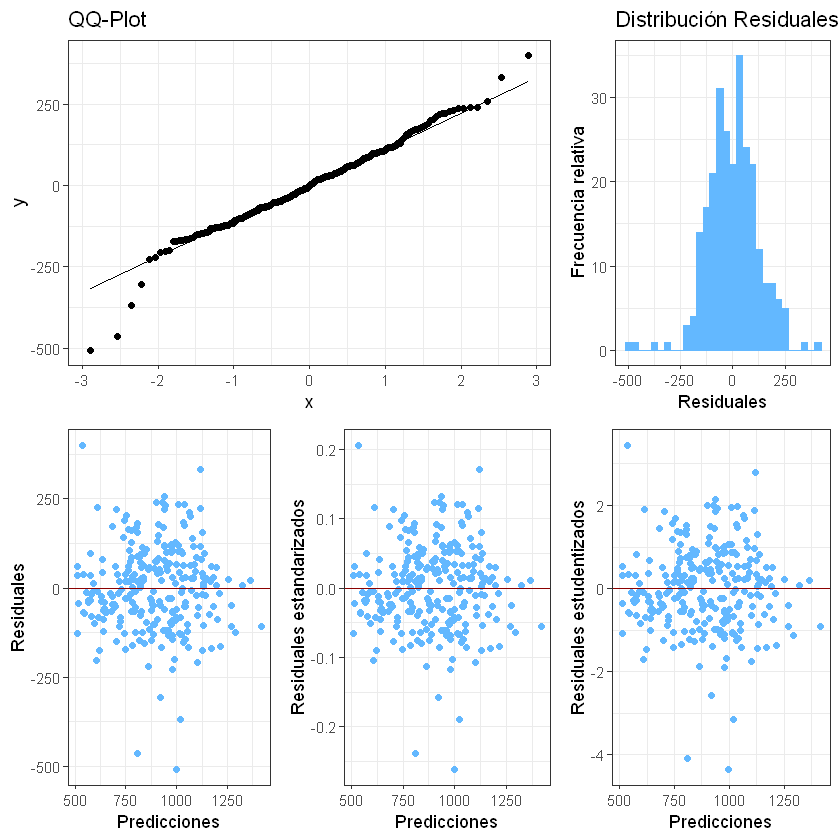
Gráficos de los residuales:
library(ggplot2)
p1 <- ggplot() +
geom_histogram(aes(x = residuales), color = "#63B8FF", fill = "#63B8FF", bins = 30) +
labs(title = "Distribución Residuales",
x = "Residuales",
y = "Frecuencia relativa") +
theme_bw()
p2 <- ggplot(data = data.frame(residuales),
aes(sample = residuales)) +
stat_qq() +
stat_qq_line() +
labs(title = "QQ-Plot") +
theme_bw()
p3 <- ggplot(data = data.frame(regression$fitted.values, residuales),
aes(x = regression$fitted.values, y = residuales)) +
geom_point(color = "#63B8FF") +
geom_hline(yintercept = 0, color = "darkred") +
labs(x = "Predicciones", y = "Residuales") +
theme_bw()
p4 <- ggplot(data = data.frame(regression$fitted.values, residuales_stan),
aes(x = regression$fitted.values, y = residuales_stan)) +
geom_point(color = "#63B8FF") +
geom_hline(yintercept = 0, color = "darkred") +
labs(x = "Predicciones", y = "Residuales estandarizados") +
theme_bw()
p5 <- ggplot(data = data.frame(regression$fitted.values, residuales_student),
aes(x = regression$fitted.values, y = residuales_student)) +
geom_point(color = "#63B8FF") +
geom_hline(yintercept = 0, color = "darkred") +
labs(x = "Predicciones", y = "Residuales estudentizados") +
theme_bw()
library(gridExtra)
grid.arrange(p1, p2, p3, p4, p5, ncol = 3,
layout_matrix = cbind(c(2,3), c(2,4), c(1,5)))
Warning message:
"package 'gridExtra' was built under R version 4.1.3"