ANOVA
Prueba de significancia de la regresión:
Con esta prueba se busca determinar si existe una relación lineal entre \(y\) y alguna de las variables regresosas \(x_j\). Este procedimiento es una prueba de adecuación del modelo.
Pruebas de hipótesis:
En \(H_1\) se cumple con al menos una \(j\) es diferente de cero, indica que al menos un coeficiente Beta cumple. Rechazar la hipótesis nula implica que al menos una regresora contribuye al modelo de forma significativa. El procedimiento para esta prueba es el análisis de varianza o también llamado ANOVA.
Análisis de varianza:
Este método se usa para probar el significado de la regresión. Aporta información adicional sobre qué tan bien funciona el modelo de regresión.
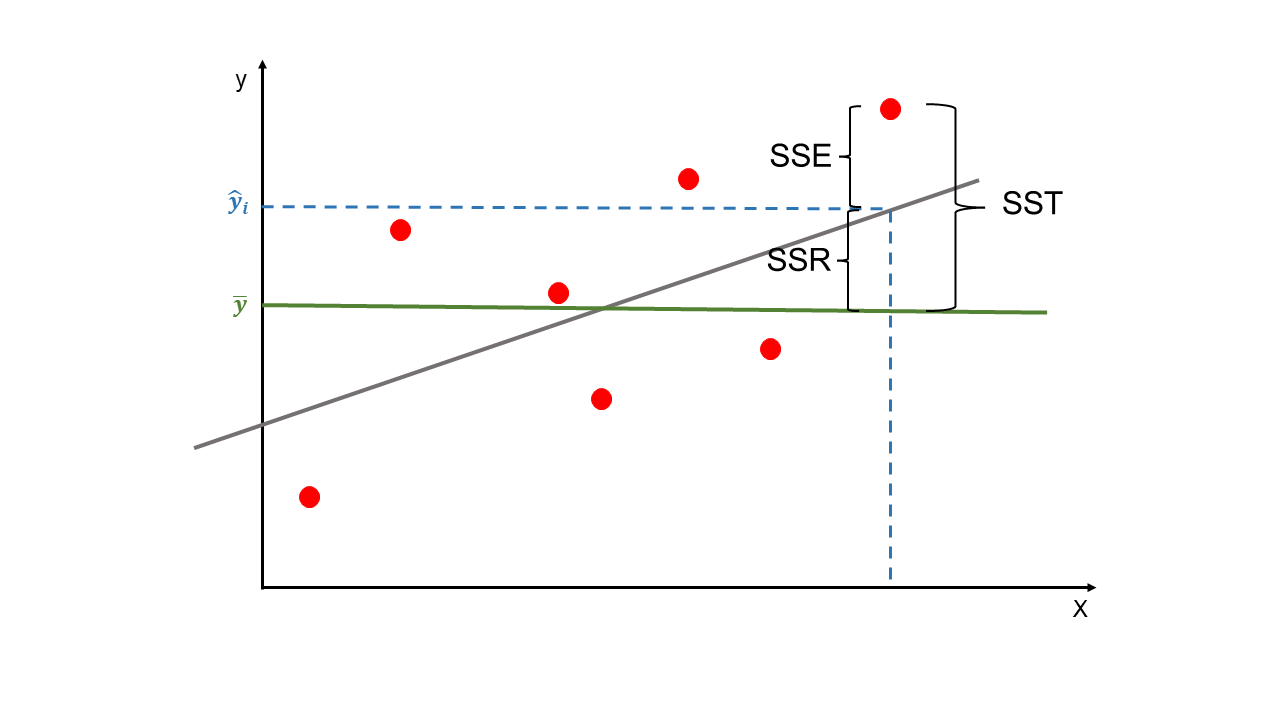
Se basa en una partición de la variabilidad total de la variable \(y\) en dos.
La variabilidad total la denotaremos como \(SST\), es la suma de las diferencias al cuadrado de las observaciones con respecto a la media.
\(SST\) es el sumatoria del cuadrado del error de la predicción, \(\varepsilon_i^2=\sum{y_i-\overline{y_i}}\), que es una medida de la variabilidad de \(y\) sin considerar el efecto de las variables regresoras. \(SST\) se puede descomponer en dos: variabilidad por la regresión, \(SSR\), y en variabilidad residual que queda sin explicar, \(SSE\). \(SSE\) es una medida de variabilidad de \(y\) que queda después de haber tenido en consideración a las variables regresoras.
Variabilidad Tota = Variabilidad Explicada + Variabilidad no Explicada.
SST
\(SSR\) también podría considerarse como la mejora en la predicción sobre la media de los datos de las variables explicativas.
\(SSE\) es la variabilidad sobrante en \(y\) después de tener en cuenta las variables explicativas o regresoras.
Se asume que toda la variación en \(y\) se tiene en cuenta con la variabilidad en las variables regresoras, \(SSR\), y con la variabilidad aleatoria \(SSE\); sin embargo, esto no descarta que se pueda hacer otras variables que expliquen porciones de la variabilidad de \(y\).
Ahora, se debe usar las estadísticas de bondad de ajuste para evaluar qué parte de la variabilidad en la variable :math:`y` es representada por el modelo de regresión lineal múltiple.
\(R^2\) coeficiente de determinación:
\(R^2\) se encuentra entre cero y uno, donde cero indica que \(SSR\) es cero y el uno indica que \(SSR = SST\) con \(SSE = 0\). Un \(R^2\) denota que las variables explicativas predicen perfectamente la variable resultados \(y\), esto es que la predicción perfecta indica que las observaciones caen directamente en la línea del ajuste lineal (esto para RLS), para RLM las observaciones caen en el plano del ajuste del modelo.
\(R^2\) ajustado:
El \(R^2\) ajustado es el mismo \(R^2\), pero ajustado por el número de variables regresoras en el modelo. El \(R^2\) ajustado puede disminuir al incluir más variables.
Donde,
\(n\): tamaño de la muestra. Número de observaciones por cada variable.
\(k\): número de variables explicativas en el modelo.
Los valores de \(R^2\) siguen una distribución \(F\). Esta distribución tiene dos grados de libertad, conocidos como los grados de libertad del numerador y del denominador. Los grados de libertad de numerador, es el número de variables explicativas \(k\) del modelo y los grados de libertad de denominador es el tamaño de la muestra \(n\) menos el número de variables explicativas \(k\) menos uno \((n-k-1)\).
A continuación se muestra la tabla ANOVA (Analysis of Variance). Esta tabla muestra los valores para \(SST\), \(SSR\), \(SSE\) y la forma para calcular el estadístico \(F\).
ANOVA
Así que:
Con el análisis de varianza se calcula el estadístico de prueba \(F_0\) para aceptar o rechazar la hipótesis hula \(H_0\). Si \(F_0\) es grande, es probable que al menos una \(\beta \neq 0\), es decir, se rechaza la hipótesis nula.
\(H_0\) se rechaza si:
Un valor relativamente grande de \(F\) y un \(Valor-p\) pequeño, proporcionan evidencia de que el \(R^2\) es mayor que cero.
El analista puede utilizar el \(R^2\) o \(R^2_{adj}\) y la prueba \(F\) para determinar la importancia del modelo. Una posible conclusión podría ser la siguiente: el modelo representa el 70% de la variabilidad y este porcentaje es significativamente mayor que cero. Esta frase se cumple con un \(R^2\) o \(R^2_{adj}\) igual a 0,70 y que \(F\) sea los suficientemente grande y además, un \(Valor-p\) pequeño.
MSE:
Con los valores de la tabla ANOVA podemos calcular el MSE (Mean Squared Error) que es el error cuadrático medio.
En el MSE, el \(SSE\) se divide por los grados de libertad, \(n-k-1\). El MSE también se denomina varianza residual \(\sigma^2\), que cuantifica la varianza de los residuales.
De esta forma, la varianza de los residuos es el MSE, entonces, la desviación estándar de los residuos es la raíz cuadrada del MSE y se denota RMSE (root-mean-square error).
Las métricas MSE y RMSE también se emplean como estadísticas de bondad de ajuste porque valores pequeños indican menor variación en los residuos del modelo. Esto sería que los valores predichos están más cerca, en promedio, de los valores reales y, por tanto, el modelo está haciendo un mejor trabajo al predecir la variable \(y\).
Código en R:
datos = read.csv("DatosCafe.csv", sep = ";", dec = ",", header = T)
print(head(datos))
Fecha PrecioInterno PrecioInternacional Producción Exportaciones TRM
1 ene-00 371375 130.12 658 517 1923.57
2 feb-00 354297 124.72 740 642 1950.64
3 mar-00 360016 119.51 592 404 1956.25
4 abr-00 347538 112.67 1055 731 1986.77
5 may-00 353750 110.31 1114 615 2055.69
6 jun-00 341688 100.30 1092 869 2120.17
EUR
1 1916.0
2 1878.5
3 1875.0
4 1832.0
5 1971.5
6 2053.5
Ajuste del modelo:
regression <- lm(Exportaciones ~ Producción + PrecioInternacional + PrecioInterno + TRM + EUR, data = datos)
summary(regression)
Call:
lm(formula = Exportaciones ~ Producción + PrecioInternacional +
PrecioInterno + TRM + EUR, data = datos)
Residuals:
Min 1Q Median 3Q Max
-507.57 -73.29 -2.66 74.68 400.44
Coefficients:
Estimate Std. Error t value Pr(>|t|)
(Intercept) 2.800e+02 1.172e+02 2.390 0.0176 *
Producción 5.806e-01 3.284e-02 17.681 <2e-16 *
PrecioInternacional -1.045e+00 6.248e-01 -1.673 0.0956 .
PrecioInterno 1.878e-04 1.311e-04 1.432 0.1533
TRM -3.049e-02 5.367e-02 -0.568 0.5704
EUR 5.335e-02 2.725e-02 1.958 0.0513 .
---
Signif. codes: 0 '*' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
Residual standard error: 121.1 on 258 degrees of freedom
Multiple R-squared: 0.7055, Adjusted R-squared: 0.6998
F-statistic: 123.6 on 5 and 258 DF, p-value: < 2.2e-16
Tabla ANOVA:
anova <- anova(regression)
print(anova)
Analysis of Variance Table
Response: Exportaciones
Df Sum Sq Mean Sq F value Pr(>F)
Producción 1 8556536 8556536 583.4640 < 2.2e-16 *
PrecioInternacional 1 3278 3278 0.2235 0.6368
PrecioInterno 1 439697 439697 29.9826 1.033e-07 *
TRM 1 9752 9752 0.6650 0.4156
EUR 1 56227 56227 3.8341 0.0513 .
Residuals 258 3783586 14665
---
Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1
\(k\): cantidad de variables explicativas.
k <- length(regression$coefficients) - 1
print(k)
[1] 5
\(n\): tamaño de la muestra.
n <- length(regression$residuals)
print(n)
[1] 264
Suma de cuadrados - Sum Sq:
SS <- anova$`Sum Sq`
print(SS)
[1] 8556536.044 3277.966 439697.106 9752.074 56226.905 3783586.184
Cuadrado medio - Mean Sq:
MS <- anova$`Mean Sq`
print(MS)
[1] 8556536.044 3277.966 439697.106 9752.074 56226.905 14665.063
F - F value:
F <- anova$`F value`
print(F)
[1] 583.4639921 0.2235221 29.9826270 0.6649868 3.8340719 NA
Valor-p para F - Pr(>F):
p_value <- anova$`Pr(>F)`
print(p_value)
[1] 3.498183e-68 6.367690e-01 1.033471e-07 4.155571e-01 5.129843e-02
[6] NA
SSR:
SSR <- sum((regression$fitted.values - mean(datos[, "Exportaciones"]))^2)
print(SSR)
[1] 9065490
print(sum(SS[0:k])) # Suma de los SS sin contar el de los Residuales.
[1] 9065490
SSE:
SSE <- sum(regression$residuals^2)
print(SSE)
[1] 3783586
SST:
SST <- SSR + SSE
print(SST)
[1] 12849076
\(R^2\):
R2 <- SSR/SST
print(R2)
[1] 0.7055363
R2 <- 1 - SSE/SST
print(R2)
[1] 0.7055363
\(R^2\) ajustado:
R2_adj <- (R2-k/(n-1))*((n-1)/(n-k-1))
print(R2_adj)
[1] 0.6998297
\(F_0\):
F <- (SS[1:k])/(SS[k+1]/(n-k-1))
print(F)
[1] 583.4639921 0.2235221 29.9826270 0.6649868 3.8340719
MSE - \(\sigma^2\):
MSE <- SSE/(n-k-1)
print(MSE)
[1] 14665.06
\(F_0\): con \(\sigma^2\)
print(SS[1:k]/MSE)
[1] 583.4639921 0.2235221 29.9826270 0.6649868 3.8340719
RMSE:
RMSE <- sqrt(MSE)
print(RMSE)
[1] 121.0994