Pronóstico con AR

Supongamos que estamos en el período con índice $h$ y el pronóstico se realiza para el período $h+\ell$, donde $\ell \geq 1$. El índice $h$ es llamado origen del pronóstico (forecast origin) y $\ell$ es el horizonte de pronóstico (forecast horizon).

Así que, $\hat{z_h}(\ell)$ es la predicción de $z_{h+\ell}$.

El pronóstico se realiza con el modelo AR(p) ajustado y con la información histórica disponible que la llamaremos $F_h = \{ z_h, z_{h-1}, z_{h-2},...\}$

Pronóstico para un paso hacia adelante:

El modelo AR(p) para pronosticar un período hacia adelante (1-Step Ahead Forecast), donde $\ell = 1$, para el período $h+1$, es:

\[z_{h+1} = \phi_0+\phi_1 z_h+\phi_2 z_{h-1} + ... + \phi_p z_{h+1-p} + a_{h+1}\]

El ajuste de $z_{h+1}$ es $\hat{z_h}(1)$, que es el ajuste del modelo AR(p) para un período hacia adelante.

\[\hat{z_h}(1) = E(z_{h+1}|F_h) = \phi_0+\sum_{i=1}^p{\phi_i z_{h+1-i}}\]

Donde,

\[e_h(1) = z_{h+1}-\hat{z_h}(1) = a_{h+1}\]

La varianza del error de predicción de un período hacia adelante es:

\[Var[e_h(1)] = Var(a_{h+1}) = \sigma_a^2\]

Como $a_t$ se distribuye normal, entonces un intervalo del 95% para el período pronosticado es $\hat{z_h}(1) \pm 1,96 \times \sigma_a$

Pronóstico para dos pasos hacia adelante:

El modelo AR(p) para pronosticar dos períodos hacia adelante (2-Step Ahead Forecast), donde $\ell = 2$, para el período $h+2$, es:

\[z_{h+2} = \phi_0+\phi_1 z_h+\phi_2 z_{h-1} + ... + \phi_p z_{h+2-p} + a_{h+2}\]

El ajuste de $z_{h+2}$ es $\hat{z_h}(2)$, que es el ajuste del modelo AR(p) para dos períodos hacia adelante.

\[\hat{z_h}(2) = E(z_{h+2}|F_h) = \phi_0+\phi_1 \hat{z_h}(1) + \phi_2 z_h + ... + \phi_p z_{h+2-p}\]

El error de la predicción es:

\[e_h(2) = z_{h+2}-\hat{z_h}(2) = \phi_1[z_{h+1}-\hat{z_h}(1)]+a_{h+2}\]

\[e_h(2) = a_{h+2}+\phi_1 a_{h+1}\]

La varianza del error del pronóstico:

\[Var[e_h(2)] = (1+\phi_1^2)\sigma_a^2\]

El intervalo del pronóstico puede ser calculado de la misma forma que el anterior, $z_{h+1}$.

En estos modelos se cumple que $Var[e_h(2)] \geq Var[e_h(1)]$. Esto significa que a medida que aumenta el horizonte de pronóstico, también aumenta la incertidumbre del pronóstico. En otras palabras, tenemos más incertiducmbre acerca de $z_{h+2}$ que de $z_{h+1}$.

Pronóstico para múltiples pasos hacia adelante:

En general, tememos:

\[z_{h+\ell} = \phi_0+\phi_1 z_{h+\ell -1} + ... + \phi_p z_{h+\ell-p}+a_{h+\ell}\]

El modelo estimado para el pronóstico sería:

\[\hat{z_h}(\ell) = \phi_0+\sum_{i=1}^p{\phi_i \hat{z_h}(\ell -i)}\]

Para $i=1,2,3,...,\ell-1$

El error de predicción en el período $h+\ell$ es:

\[e_h(\ell) = z_{h+\ell} - \hat{z_h}(\ell)\]

Es fácil demostrar que cuando $\ell \rightarrow \infty$, es decir, pronosticar muchos períodos hacia adelante, $\hat{z_h}(\ell)$ converge a $E[z_t]$. El pronóstico puntual a largo plazo se aproxima a su media incondicional. Esta propiedad se conoce como reversión a la media.

Para el modelo AR(1), la velocidad de reversión a la media se mide como $k = ln(\frac{0,5}{|\phi_1|})$ y la varianza del error del pronóstico se aproxima a la varianza de $z_t$

Código en `R` para pronosticar modelos AR:

library(forecast)

Warning message:
"package 'forecast' was built under R version 4.1.3"
Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo

estacional <- read.csv("Estacionalidad.csv", sep = ",", dec = ".", header = T)
estacional2 <- read.csv("Estacionalidad2.csv", sep = ",", dec = ".", header = T)
tendencia <- read.csv("Tendencia.csv", sep = ",", dec = ".", header = T)
ruidoblanco <- read.csv("ruidoblanco.csv", sep = ",", dec = ".", header = T)

library(ggplot2)

Ejemplo 1: serie estacional

ggplot()+geom_line(aes(x = c(1:nrow(estacional)), y = estacional[,1]), size = 0.7)+
        theme_minimal() +
        labs(title = "Serie de tiempo 1", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

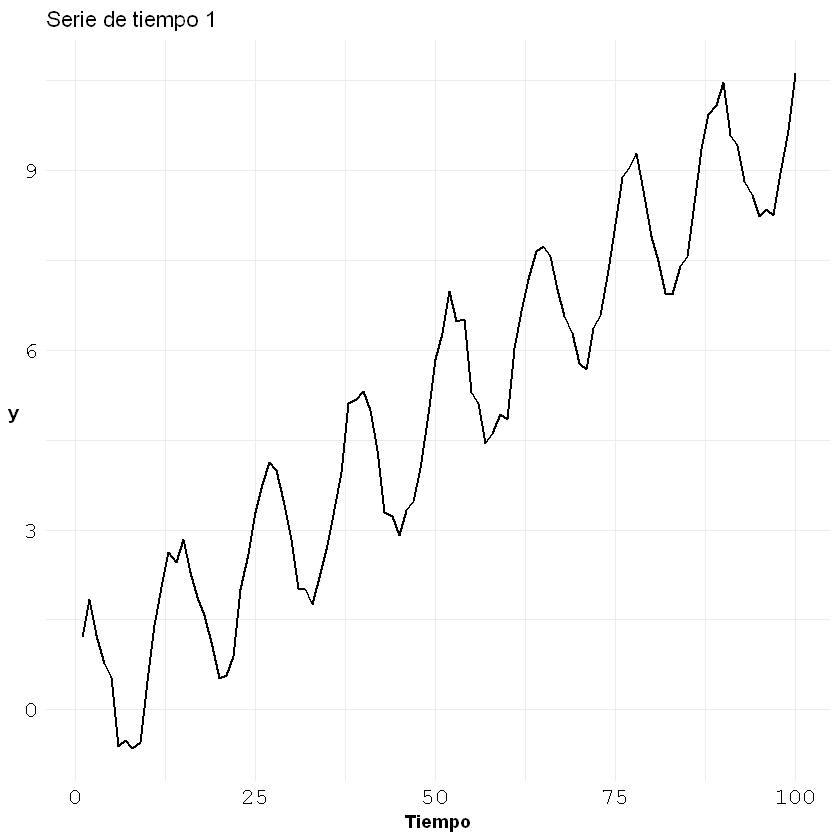
pacf(estacional[,1], main = "Serie de tiempo 1")

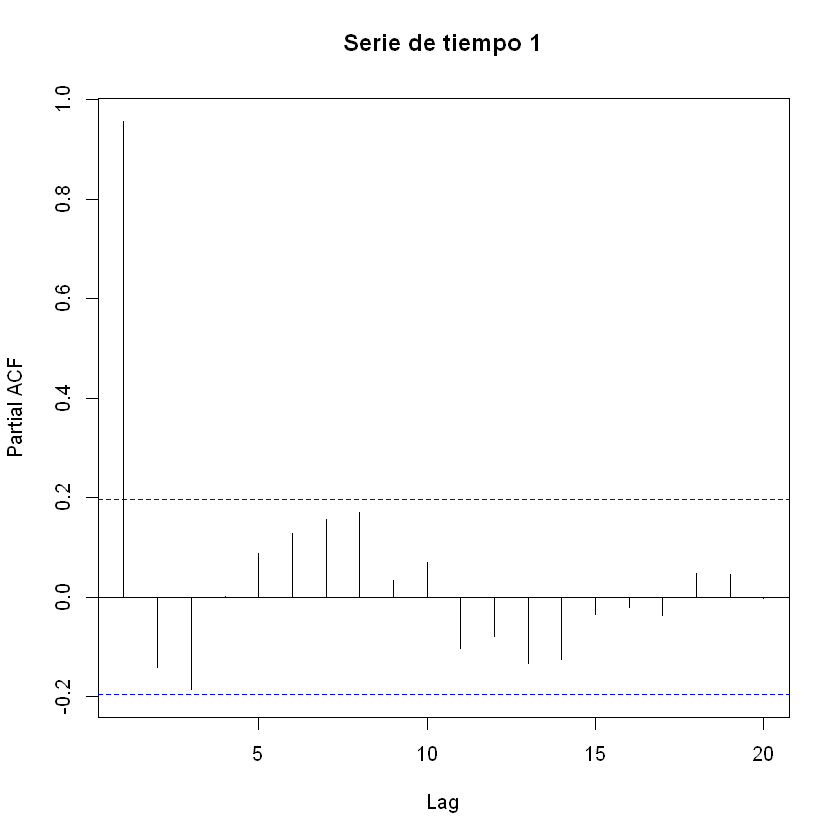
Ajuste modelo AR(1):

ar <- arima(estacional[,1], order = c(1, 0, 0))
ar

Call:
arima(x = estacional[, 1], order = c(1, 0, 0))

Coefficients:
         ar1  intercept
      0.9895     5.5923
s.e.  0.0118     3.2046

sigma^2 estimated as 0.3253:  log likelihood = -87.68,  aic = 181.36

Antes de realizar el pronóstico podemos ajustar el modelo AR(1) a las observaciones de la serie de tiempo original.

El modelo estimado es:

\[\hat{z_t} = 0,9895 z_{t-1}\]

El coeficiente $\phi_1$ se extrae con $coef[1].

phi_1 <- ar$coef[1]
print(phi_1)

      ar1
0.9894924

z <- estacional[,1]
p <- 1              # AR (1)

fitted <- vector()  # vector para almacenar los valores ajustados sobre la serie de tiempo

for(k in length(z):2){

    fitted[k] <- phi_1*z[k-p]
}
print(head(fitted))  # El primer término es NA porque no hay más datos históricos

[1]        NA 1.1900454 1.8174858 1.2311345 0.7646015 0.5281369

Gráfico de la serie original con los valores ajustados:

ggplot()+geom_line(aes(x = c(1:nrow(estacional)), y = estacional[,1]), size = 0.7)+
        geom_line(aes(x = c(1:nrow(estacional)), y = fitted), col = "red")+
        theme_minimal() +
        labs(title = "Serie de tiempo 1", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

Warning message:
"Removed 1 row(s) containing missing values (geom_path)."

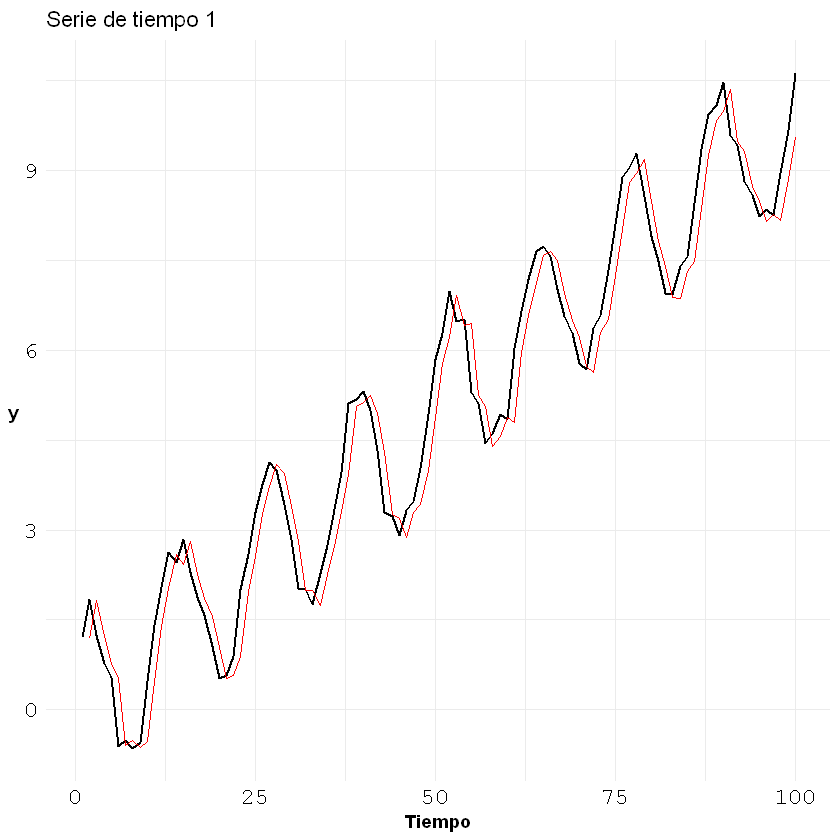
El ajuste anterior, sobre la serie de tiempo, se puede hacer con la función fitted().

print(head(fitted(ar))) # Hay una diferencia con el cálculo manual porque se usan diferente cantidad de decimales.

Time Series:
Start = 1
End = 6
Frequency = 1
[1] 1.8373579 1.2488073 1.8762477 1.2898964 0.8233634 0.5868988

Pronóstico (Forecasting):

Se usa la función forecast(). Se debe indicar lo siguiente:

h =: cantidad de períodos hacia adelante para pronosticas $(\ell)$.
level =: intervalo de confianza para el pronóstico. Usualmente es 95% o 99%.

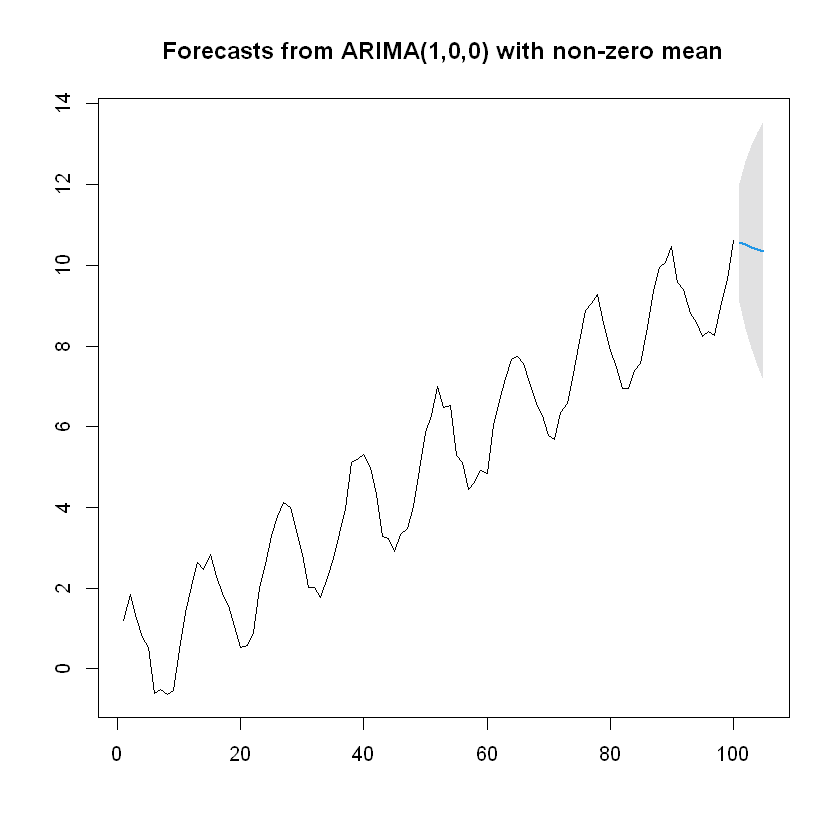
Pronóstico para 5 períodos hacia adelante:

La serie de tiempo tiene $N=100$ y como $\ell = 5$, entonces los $\hat{z_h}(\ell)$ con su respectivo intervalo de confianza al 99% son:

forecast <- forecast(ar, h = 5, level = 99)
forecast

    Point Forecast    Lo 99    Hi 99
     10.55864 9.089502 12.02777
     10.50645 8.439670 12.57323
     10.45482 7.936753 12.97288
     10.40372 7.511242 13.29620
     10.35317 7.136040 13.57029

plot(forecast)

Pronóstico para 10 períodos hacia adelante:

forecast <- forecast(ar, h = 10, level = 99)
forecast

    Point Forecast    Lo 99    Hi 99
     10.55864 9.089502 12.02777
     10.50645 8.439670 12.57323
     10.45482 7.936753 12.97288
     10.40372 7.511242 13.29620
     10.35317 7.136040 13.57029
     10.30314 6.797162 13.80912
     10.25364 6.486244 14.02104
     10.20466 6.197802 14.21152
     10.15620 5.928000 14.38439
     10.10824 5.674025 14.54246

plot(forecast)

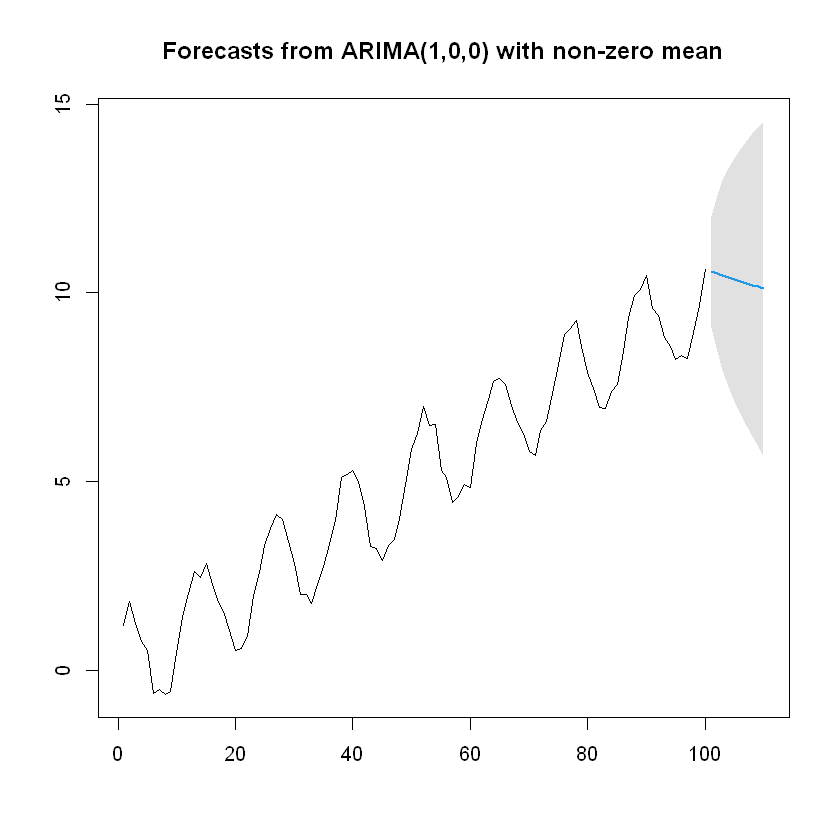
Predicciones:

Las predicciones se pueden extraer con $mean.

print(forecast$mean)

Time Series:
Start = 101
End = 110
Frequency = 1
 [1] 10.55864 10.50645 10.45482 10.40372 10.35317 10.30314 10.25364 10.20466
 [9] 10.15620 10.10824

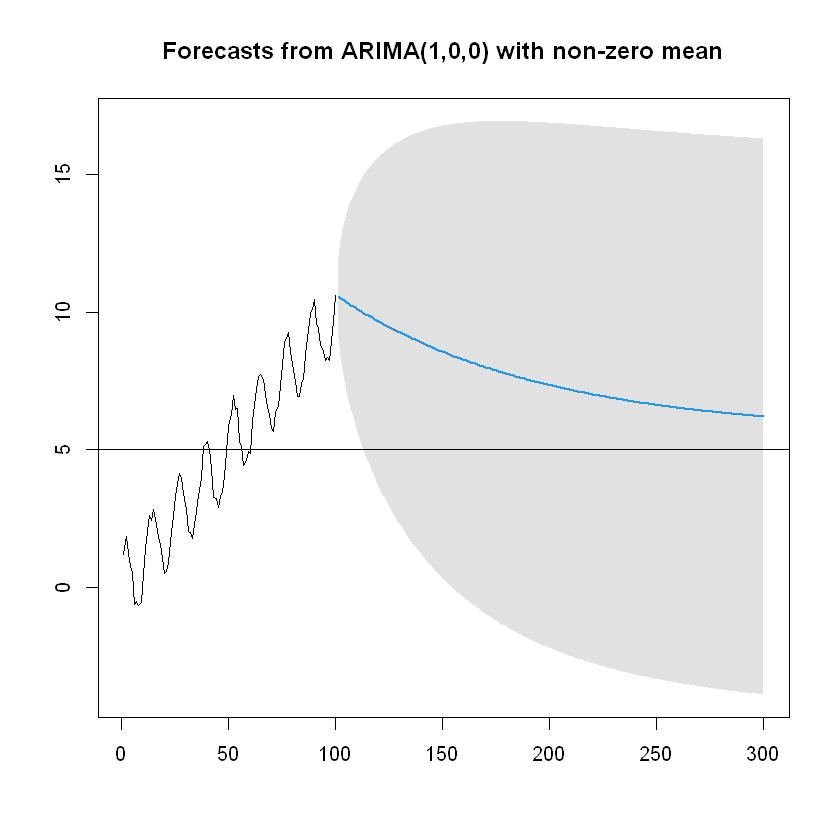
Los modelos AR(p) tienen una reversión a la media de la serie original. Pronosticar muchos períodos hacia adelante, $\hat{z_h}(\ell)$ converge a $E[z_t]$. Hagamos el ejemplo de pronosticar 200 períodos hacia adelante.

forecast <- forecast(ar, h = 200, level = 99)
plot(forecast)
abline(h = mean(estacional[,1]))

Ejemplo 2: serie estacional, varianza no cosntante

pacf(estacional2[,2], main = "Serie de tiempo 2")

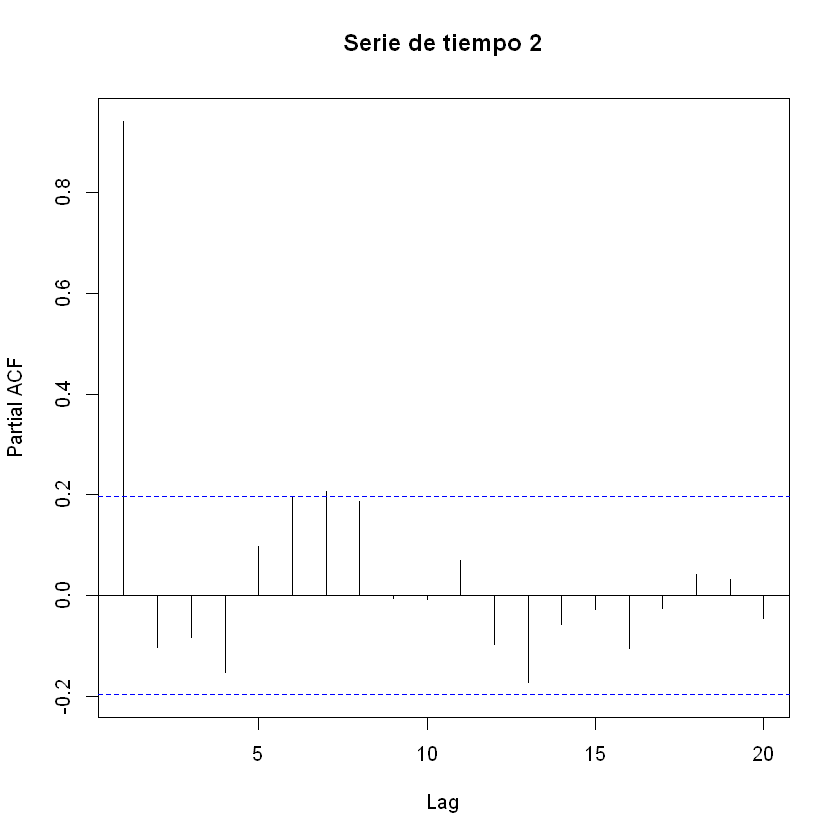
Ajuste modelo AR(1):

ar <- arima(estacional2[,2], order = c(1, 0, 0))
ar

Call:
arima(x = estacional2[, 2], order = c(1, 0, 0))

Coefficients:
         ar1  intercept
      0.9749     1.6177
s.e.  0.0215     0.7873

sigma^2 estimated as 0.06952:  log likelihood = -10.09,  aic = 26.17

fitted <- fitted(ar)

ggplot()+geom_line(aes(x = c(1:nrow(estacional2)), y = estacional2[,2]), size = 0.7)+
        geom_line(aes(x = c(1:nrow(estacional2)), y = fitted), col = "red")+
        theme_minimal() +
        labs(title = "Serie de tiempo 2", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

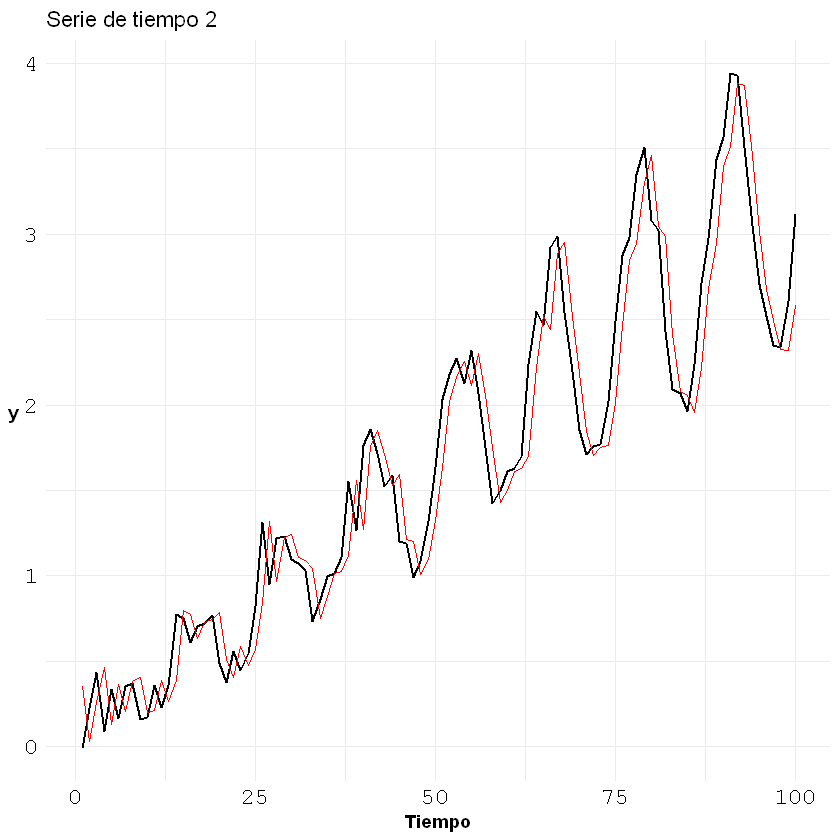
Pronóstico (Forecasting):

forecast <- forecast(ar, h = 5, level = 99)
plot(forecast)

Ejemplo 3: serie con tendencia, varianza constante

pacf(tendencia[,2], main = "Serie de tiempo 3")

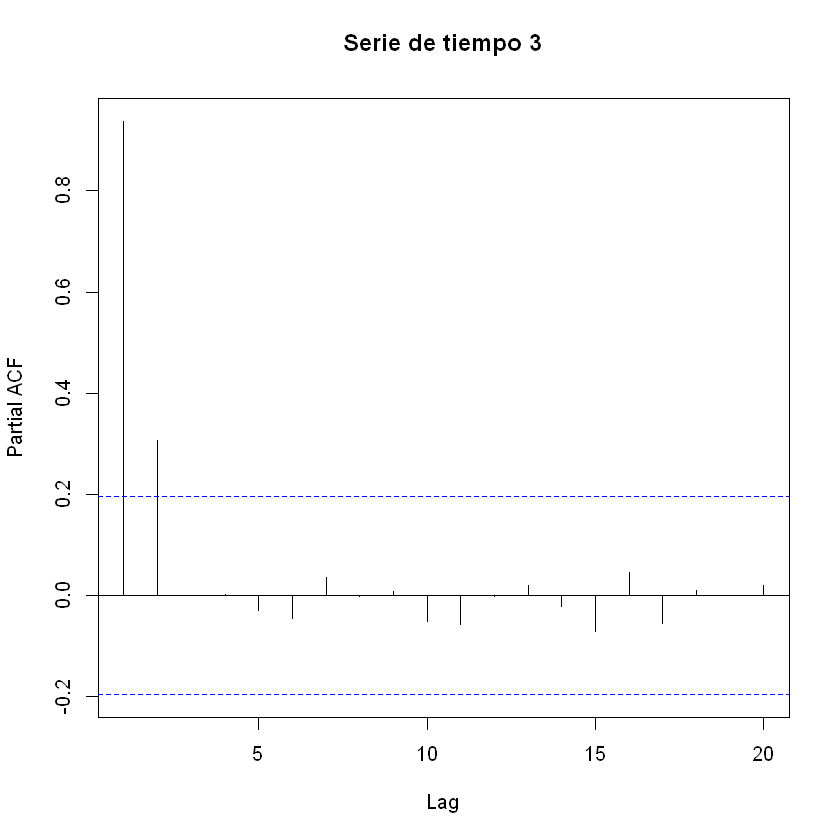
Ajuste modelo AR(2):

ar <- arima(tendencia[,2], order = c(2, 0, 0))
ar

Call:
arima(x = tendencia[, 2], order = c(2, 0, 0))

Coefficients:
         ar1     ar2  intercept
      0.4305  0.5639   985.1726
s.e.  0.0860  0.0863   839.8509

sigma^2 estimated as 14648:  log likelihood = -623.71,  aic = 1255.42

fitted <- fitted(ar)

ggplot()+geom_line(aes(x = c(1:nrow(tendencia)), y = tendencia[,2]), size = 0.7)+
        geom_line(aes(x = c(1:nrow(tendencia)), y = fitted), col = "red")+
        theme_minimal() +
        labs(title = "Serie de tiempo 3", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

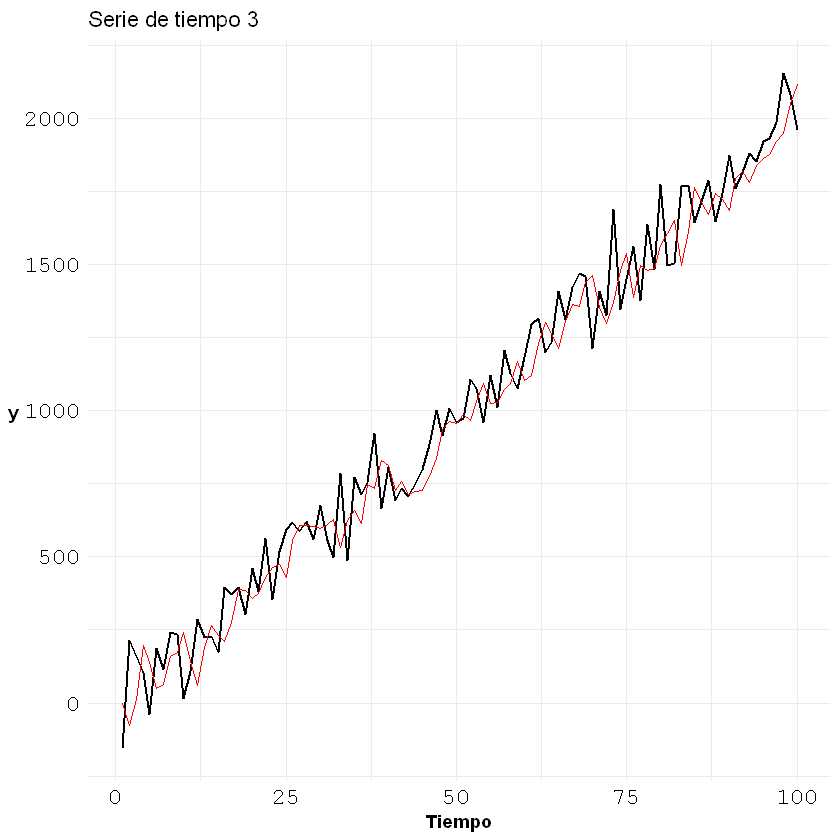
La gráfica anterior la podemos hacer de forma manual siguiente la siguiente ecuación de estimación para un AR(2):

\[\hat{z_t} = \phi_1z_{t-1}+\phi_2z_{t-2}\]

phi_1 <- ar$coef[1]
print(phi_1)

      ar1
0.4304606

phi_2 <- ar$coef[2]
print(phi_2)

      ar2
0.5638954

z <- tendencia[,2]
p <- 2              # AR (2)

fitted <- vector()  # vector para almacenar los valores ajustados sobre la serie de tiempo

for(k in length(z):3){

    fitted[k] <- phi_1*z[k-p+1] + phi_2*z[k-p]
}
print(head(fitted))

[1]         NA         NA   5.944229 189.616020 134.291362  42.786254

ggplot()+geom_line(aes(x = c(1:nrow(tendencia)), y = tendencia[,2]), size = 0.7)+
        geom_line(aes(x = c(1:nrow(tendencia)), y = fitted), col = "red")+
        theme_minimal() +
        labs(title = "Serie de tiempo 3", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

Warning message:
"Removed 2 row(s) containing missing values (geom_path)."

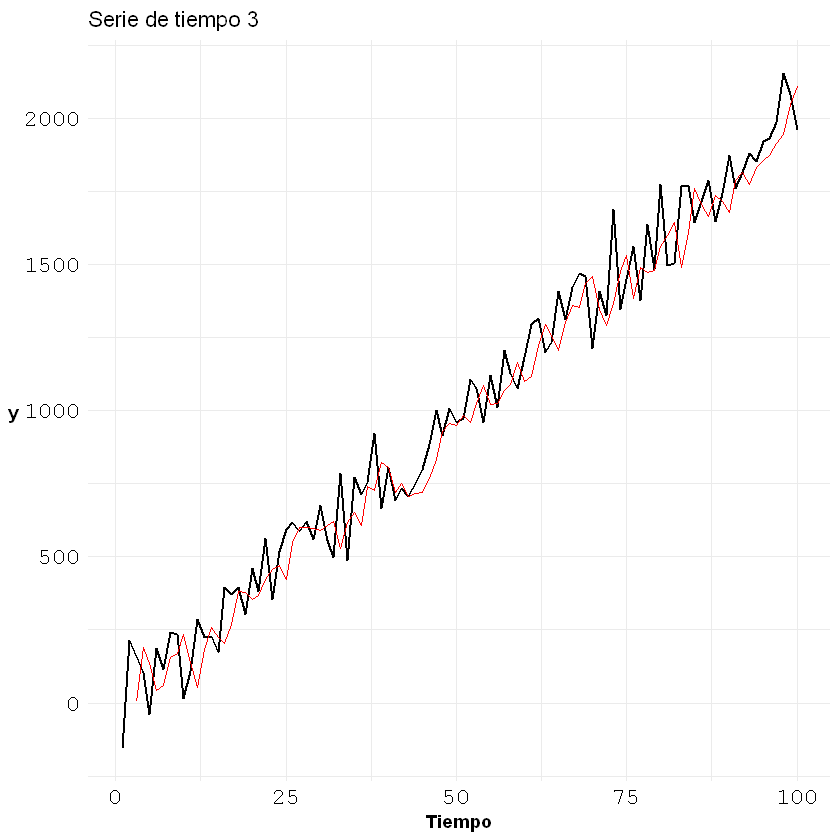
Pronóstico (Forecasting):

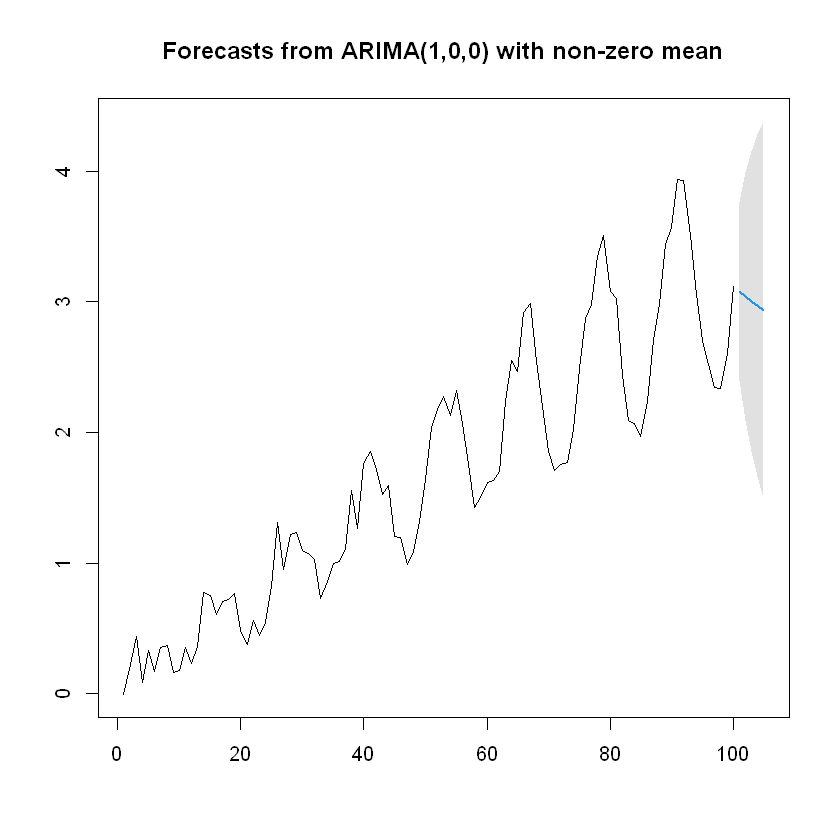
forecast <- forecast(ar, h = 5, level = 99)
plot(forecast)

Ejemplo 4: serie Ruido Blanco

Ya sabemos que no se tiene una buen ajuste a las series de tiempo ruido blanco, pero hagamos el ejercicio.

pacf(ruidoblanco[,2], main = "Serie de tiempo 4")

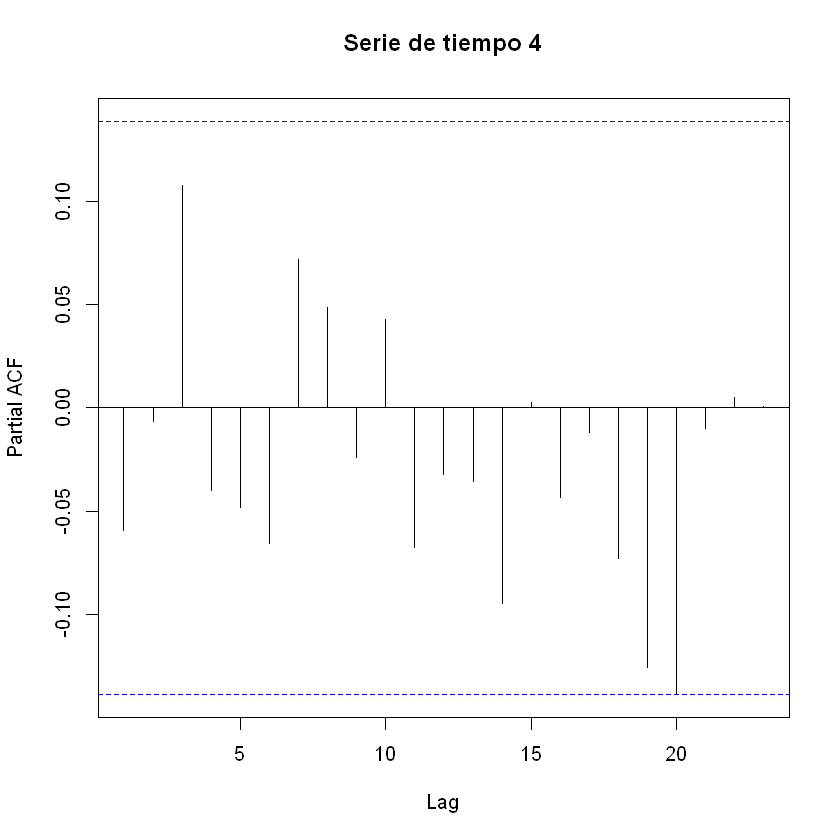
Ajuste modelo AR(1):

ar <- arima(ruidoblanco[,2], order = c(2, 0, 0))
ar

Call:
arima(x = ruidoblanco[, 2], order = c(2, 0, 0))

Coefficients:
          ar1      ar2  intercept
      -0.0600  -0.0061    -0.1104
s.e.   0.0709   0.0711     0.0683

sigma^2 estimated as 1.061:  log likelihood = -289.71,  aic = 587.42

fitted <- fitted(ar)

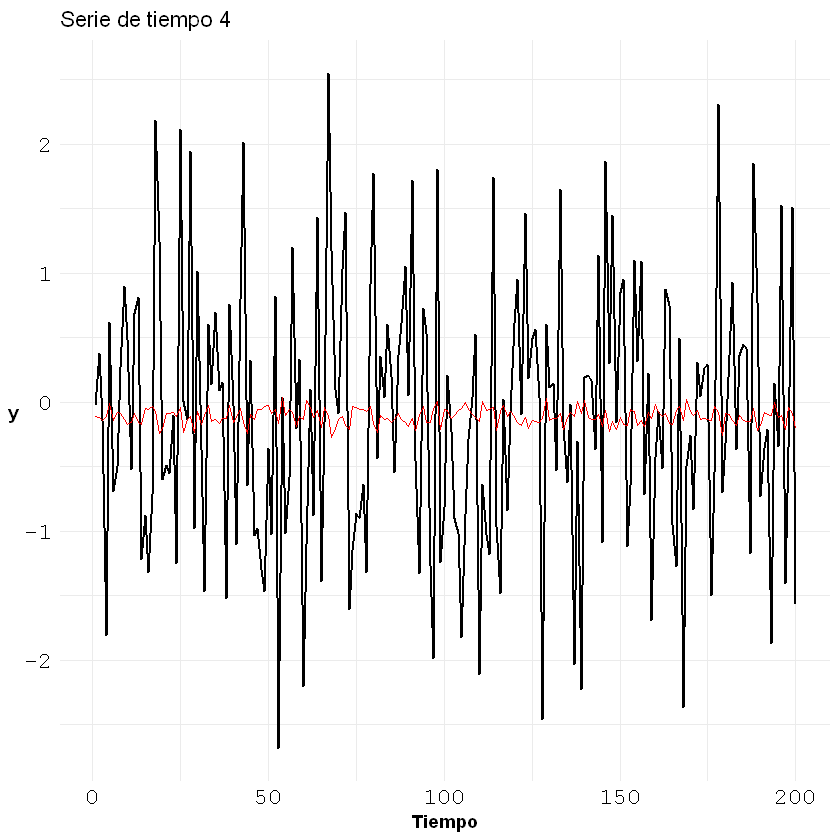
ggplot()+geom_line(aes(x = c(1:nrow(ruidoblanco)), y = ruidoblanco[,2]), size = 0.7)+
        geom_line(aes(x = c(1:nrow(ruidoblanco)), y = fitted), col = "red")+
        theme_minimal() +
        labs(title = "Serie de tiempo 4", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

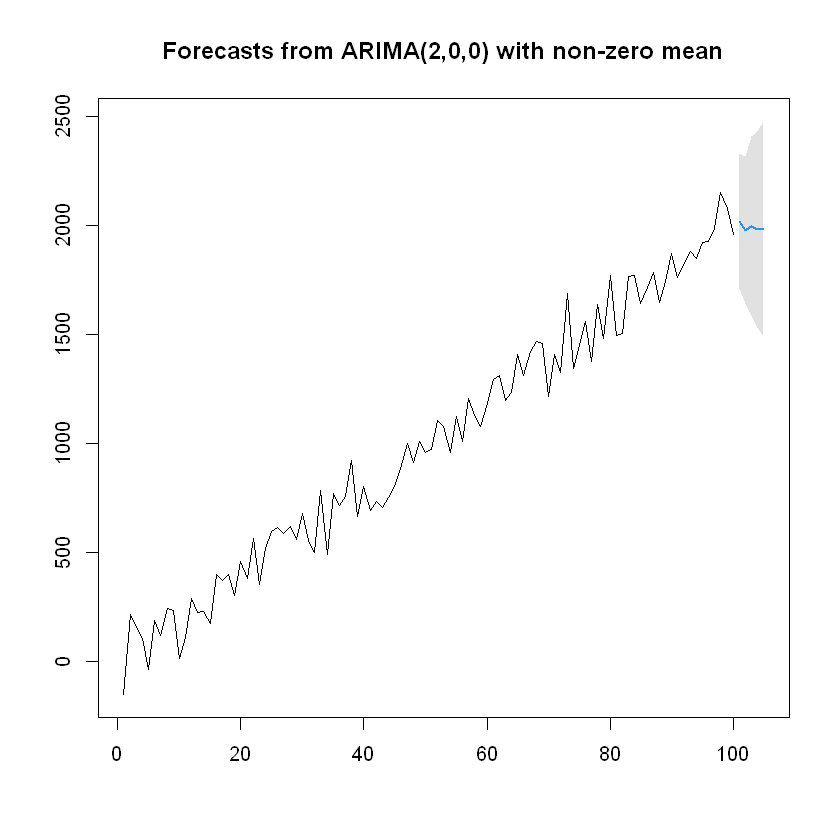
Pronóstico (Forecasting):

forecast <- forecast(ar, h = 5, level = 99)
plot(forecast)

Pronóstico con AR

Código en R para pronosticar modelos AR:

Código en `R` para pronosticar modelos AR: