Modelos de promedio móvil - MA
Los modelos de promedio móvil MA (Moving-Average) son similares a un modelo AR de orden infinito con algunas restricciones de parámetros.
En forma teórica y no realista podemos considerar un modelo AR de orden infinito como:
Este modelo no es realista porque tendría infinitos parámetros; sin embargo, se puede asumir que los coeficientes \(\phi_i\) satisfacen algunas restricciones para que estén determinados por un número finito de parámetros así:
Donde los coeficientes dependen de un solo parámetros \(\theta_1\) así: \(\phi_i = -\theta_1^i\) para \(i \geq 1\).
Para que el modelo sea estacionario, \(\theta_1\) debería ser menor que uno en valor absoluto \((|\theta_1|<1)\).
Si \(|\theta_1|<1\) entonces \(\theta_1^i \rightarrow 0\) cuando \(i \rightarrow \infty\). Esto significa que los valores más recientes tienen más impacto que los valores más antiguos.
Así que la contribución de \(zr_{t-i}\) hacia \(z_t\) decae exponencialmente cuando \(i\) incrementa. Esto es razonable en una serie de tiempo estacionario \(z_t\) donde la dependencia con los rezagos \(z_{t-i}\), si lo hay, disminuya en el tiempo.
La ecuación del modelo MA puede ser reescrita de la siguiente forma despejando \(\phi_0\) y \(a_t\):
Para \(z_{t-1}\) es:
Para MA(1):
Sabemos que para \(z_{t-1}\) el modelo es \(\phi_0+a_{t-1}\). Reescribiendo la ecuación anterior:
Despejando:
Reordenando:
La anterior ecuación indica que \(z_t\) es un promedio ponderado de las innovación \(a_t\) y \(a_{t-1}\). Este modelo es llamado MA de orden uno o simplemente MA(1). También se puede reescribir así:
\(a_t\) y \(a_{t-1}\) son incorrelacionados.
Donde \(c_0\) es una constante y \(a_t\) es ruido blanco.
Para MA(2) tenemos:
De forma general, el modelo MA(q) sería:
Propiedades de los modelos MA:
Estacionariedad:
Debido a que los modelos MA son combinaciones lineales finitas de una secuencia de ruido blanco, la media y la desviación estándar son invariantes en el tiempo.
Función de autocorrelación (ACF):
Para los modelos MA(1), la ACF del lag 1 no es cero, pero para los demás la AFC si es cero. Esto es que en el gráfico de la ACF hay un corte o caída rápida en los modelo MA(1). Los valores de la AFC para MA(1) son:
Si \(lag>1\):
Para MA(2), AFC es:
Si \(lag>2\):
Así que el corte o la caída rápida en el gráfico de la ACF en los modelo MA(2) ocurre en el lag 2.
De forma general, para los modelos MA(q), los valores de AFC del lag \(q\) no son cero, pero para \(lag>q\), \(\rho_k=0\).
Identificación del orden de MA:
Se utiliza AFC para identificar el orden del modelo MA.
Si el ACF del rezago \(q\) es diferente de cero \((\rho_q \neq 0)\), pero el AFC del rezago \(\ell\) es igual a cero \((\rho_{\ell} = 0)\), entonces la serie de tiempo sigue un modelo MA(q).
Pronóstico (Forecasting) con MA:
Para un paso hacia adelante y un MA(1), el pronóstico es:
La esperanza condicional es:
El error es:
La varianza del error es:
Para dos pasos hacia adelante y un MA(1), el pronóstico es:
La esperanza condicional es:
La varianza del error es:
La varianza de dos pasos hacia adelante es mayor o igual que el de un paso hacia adelante.
El resultado anterior muestra que para un modelo MA(1) el pronóstico de 2 pasos adelante de la serie es simplemente la media incondicional del modelo, \(c_0\). Por tanto, de forma general, \(\hat{z_h}(\ell)=c_0\) para \(\ell \geq 2\).
En resumen, en el modelo MA(1), el pronóstico de un paso es \(c_0-\theta_1a_h\) y para múltiples pasos es la media incondicional, \(c_0\), quiere decir que los modelos MA(1) tardan solo \(1\) período en reversar a la media. Similarmente ocurre con los modelo MA(2), tardan \(2\) períodos de tiempo para la reversión a la media y la varianza del error del pronóstico se aproxima a la varianza de la serie de tiempo en \(2\) pasos.
Las ecuaciones del pronóstico para MA(2) son:
Pronóstico de un paso de MA(2):
Pronóstico de dos pasos de MA(2):
Pronóstico para \(\ell\) pasos de MA(2):
En general, los modelo MA(q) con múltiples pasos de pronóstico tienen reversión a la media en \(q\) pasos.
Ajuste modelo MA en R:
ejemplo3 <- read.csv("Ejemplo3.csv", sep = ",", dec = ".", header = T)
timeserie <- ts(ejemplo3[,2])
library(ggplot2)
library(forecast)
Warning message:
"package 'forecast' was built under R version 4.1.3"
Registered S3 method overwritten by 'quantmod':
method from
as.zoo.data.frame zoo
ggtsdisplay(timeserie)
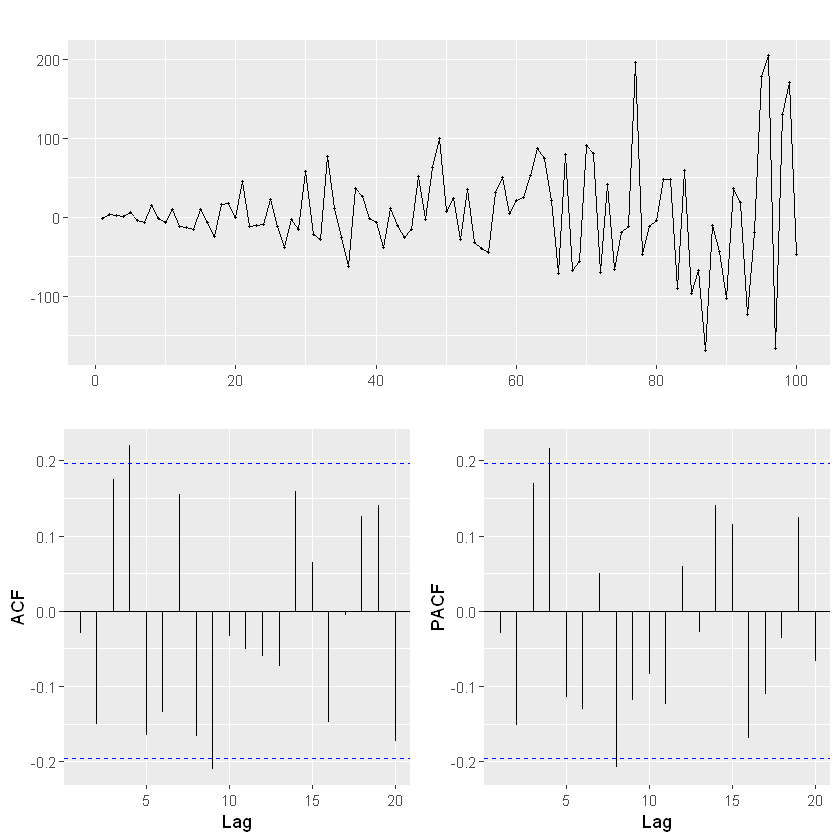
MA(4):
El orden \(q\) del MA es 4 porque en la ACF el rezago para \(k=4\) está por fuera de las bandas azules.
Las series de tiempo univaridas se ajustan en R con la función
arima() al igual que en AR. En este caso el \(q\) del modelo MA
se especifica de la siguiente manera: order = c(0, 0, q).
Para este ejemplo que solo el AFC del rezago 4 es significativo, puede comprobar que los valores de los coeficientes \(\theta_i\) menores a 4 tienen valores cercanos a cero.
ma <- arima(timeserie, order = c(0, 0, 4))
ma
Call:
arima(x = timeserie, order = c(0, 0, 4))
Coefficients:
ma1 ma2 ma3 ma4 intercept
0.0106 -0.0736 -0.0284 0.5003 4.4707
s.e. 0.0980 0.0860 0.1096 0.1323 8.1861
sigma^2 estimated as 3455: log likelihood = -549.86, aic = 1111.72
El intercepto es \(c_0\), el cual será el valor de la predicción después del período \(q=4\).
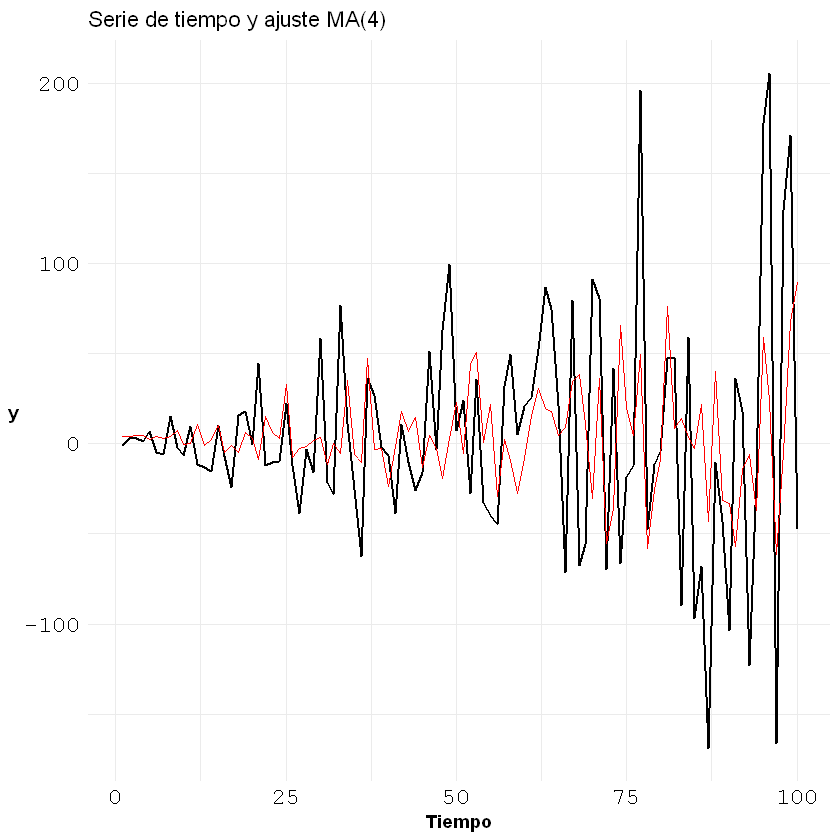
Ajuste del modelo MA(4) sobre la serie de tiempo:
fitted <- fitted(ma)
timeserie <- data.frame(timeserie)
print(fitted)
Time Series:
Start = 1
End = 100
Frequency = 1
[1] 3.8591451 4.3386383 4.7378070 4.3491948 2.4544620 3.9632828
[7] 3.0189029 3.9411836 7.3527550 -0.3321435 0.3983087 10.5825640
[13] -0.7845584 2.5968972 10.2921454 -4.9472929 -1.1056808 -4.5826421
[19] 6.3580960 2.7620419 -8.6284549 15.1849201 6.1321248 3.1146035
[25] 32.9925435 -7.7929819 -2.7259374 -1.7412458 1.8227936 3.2595544
[31] -11.6859419 0.1001768 -5.5208601 35.2187463 -5.9085283 -10.4252587
[37] 47.1471677 -3.3416601 -2.6602688 -23.5679729 -1.5832539 17.8050519
[43] 6.8829850 14.4017725 -13.0295278 4.4102354 -2.3378217 -18.9826462
[49] 2.7319509 22.9025545 -5.4657772 44.1083371 50.4301633 0.8777953
[55] 21.9883011 -29.2916874 2.4095807 -9.0211358 -27.5248529 -8.0401514
[61] 15.3708873 30.8904038 19.5639426 17.7139197 4.5638443 9.2354326
[67] 34.3396687 38.7031137 10.6132720 -30.0766319 36.2991638 -55.2676263
[73] -35.7117488 65.6735675 19.9265577 4.4740993 49.5447263 -57.8570754
[79] -25.0653399 -8.4765316 76.2881463 8.7365030 13.7946671 3.3984525
[85] -2.8100901 21.7860170 -43.0175805 40.2643433 -31.1868250 -33.2474762
[91] -56.8207929 -14.2950974 -6.0793692 -36.8126391 58.9802981 23.9358959
[97] -61.2151528 -4.5712024 67.8847135 89.2979145
ggplot()+geom_line(aes(x = c(1:nrow(timeserie)), y = timeserie[,1]), size = 0.7)+
geom_line(aes(x = c(1:nrow(timeserie)), y = fitted), col = "red")+
theme_minimal() +
labs(title = "Serie de tiempo y ajuste MA(4)", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))
Don't know how to automatically pick scale for object of type ts. Defaulting to continuous.
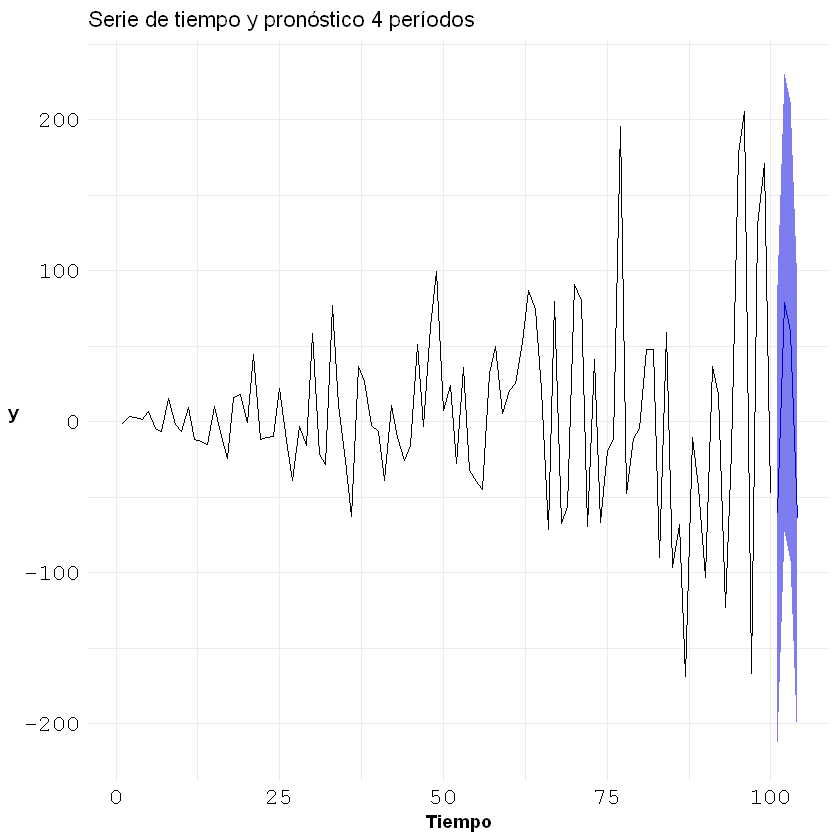
Pronósticos del modelo MA(4):
forecast <- forecast(ma, h = 4, level = 99)
forecast
Point Forecast Lo 99 Hi 99
101 -60.95020 -212.36338 90.46298
102 78.76388 -72.65782 230.18559
103 59.90433 -91.92679 211.73546
104 -64.04996 -215.94207 87.84215
autoplot(forecast)+
theme_minimal() +
labs(title = "Serie de tiempo y pronóstico 4 períodos", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))
forecast <- forecast(ma, h = 10, level = 99)
forecast
Point Forecast Lo 99 Hi 99
101 -60.950203 -212.36338 90.46298
102 78.763882 -72.65782 230.18559
103 59.904333 -91.92679 211.73546
104 -64.049957 -215.94207 87.84215
105 4.470695 -165.26055 174.20194
106 4.470695 -165.26055 174.20194
107 4.470695 -165.26055 174.20194
108 4.470695 -165.26055 174.20194
109 4.470695 -165.26055 174.20194
110 4.470695 -165.26055 174.20194
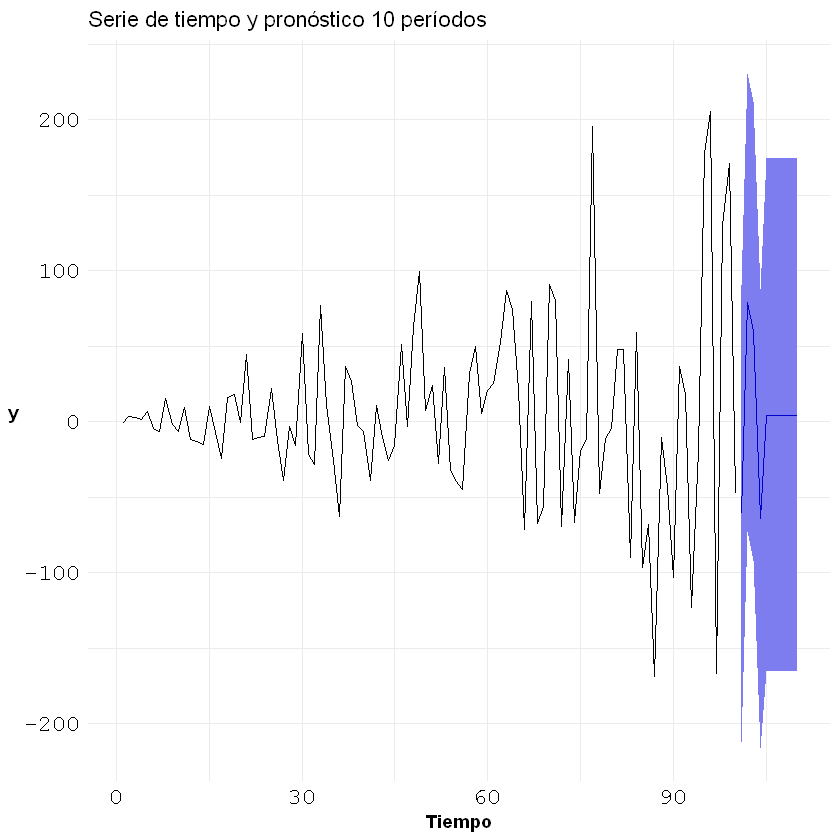
Después del 4 período hacia adelante en la predicción, el pronóstico se convierte en el intecepto que es \(c_0\).
autoplot(forecast)+
theme_minimal() +
labs(title = "Serie de tiempo y pronóstico 10 períodos", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))