Características de las series de tiempo

Las series de tiempo son datos secuenciales ordenados por el tiempo, en otras palabras, las series de tiempo son variables que dependen del tiempo. Para cada punto en el tiempo \(t\) existe un único valor de \(y\). Cada intervalo de tiempo tiene la misma distancia temporal.

Para la modelación de las series temporales primero se debe introducir los conceptos que son insumos para determinar el tipo de variable con la cual se está trabajando.

Variación estacional:

Variación estacional constante: la dimensión de los cambios estacionales es la misma. La magnitud del cambio estacional no depende del nivel de la serie de tiempo.

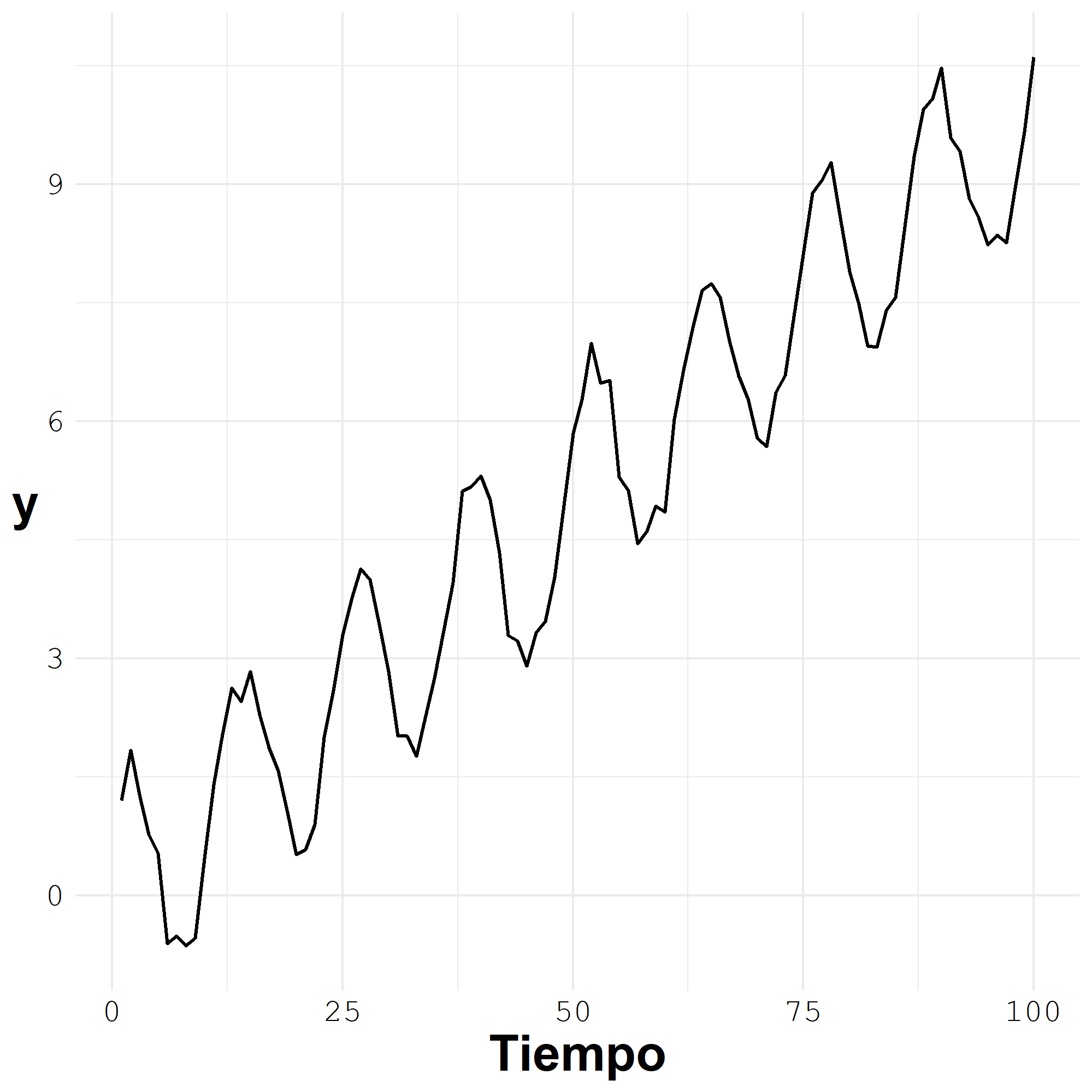
Estacionalidad

variación estacional creciente (decreciente): la magnitud del cambio estacional es mayor (menor) a través del tiempo.

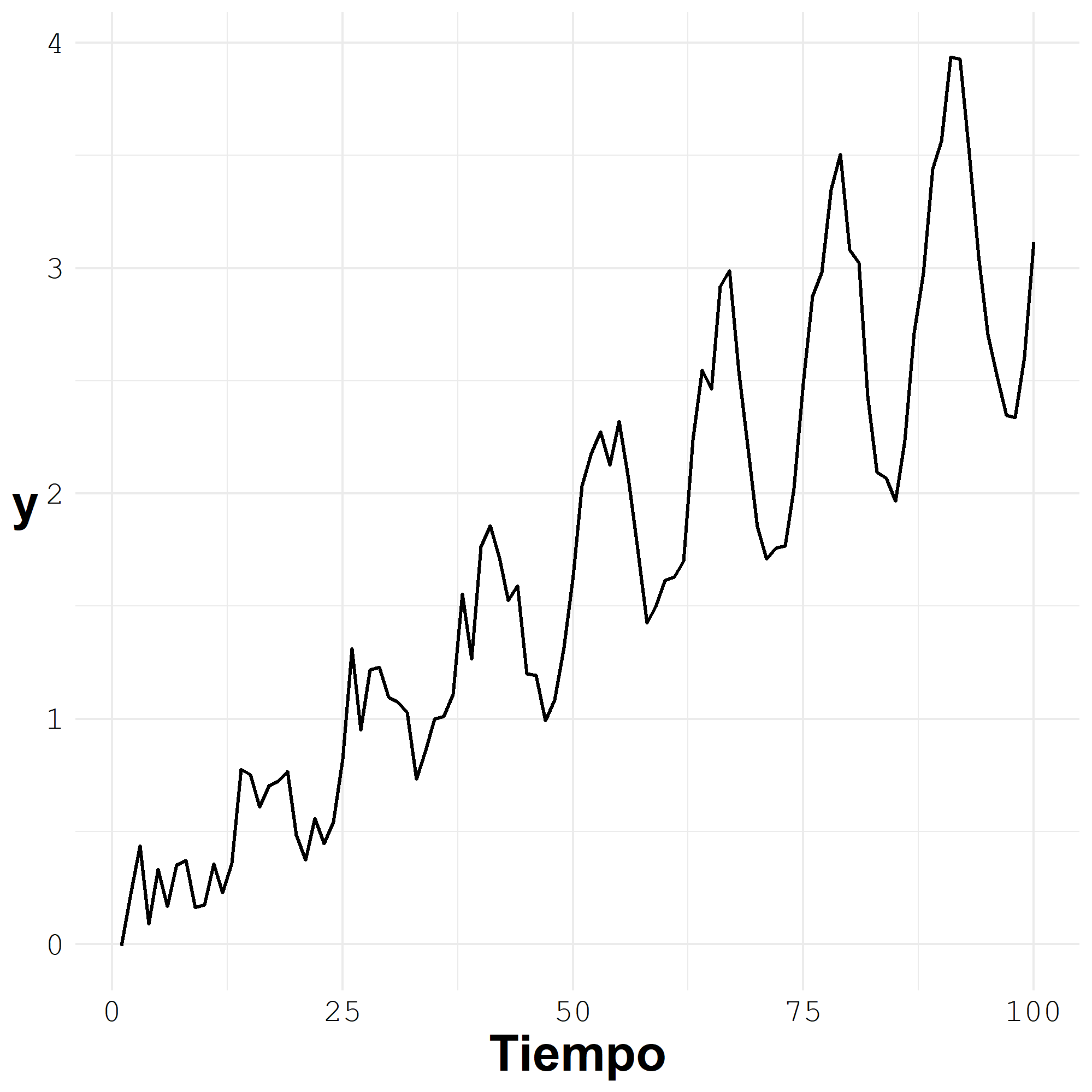
Estacionalidad2

Cuando una serie de tiempo muestra una variación estacional creciente, lo común es aplicar una transformación a los datos para generar una serie de tiempo con variación estacional constante. Se puede aplicar alguna de las siguientes transformaciones:

\(y* = y^{\lambda}\) donde \(0<\lambda<1\)

Cuando \(\lambda\) se aproxima a cero, la transformación se convierte en: \(y* = ln[y]\)

Métodos de descomposición:

Descomposición multiplicativa:

Para las series de tiempo con variación estacional creciente o decreciente.

\[y = TR_t \times SN_t \times CL_t \times IR_t\]

Donde,

\(TR_t\): componente de la tendencia en el período \(t\).

\(SN_t\): componente o factor estacional en el período \(t\).

\(CL_t\): componente o factor cíclico en el período \(t\).

\(IR_t\): componente o factor irregular en el período \(t\).

El componente cíclico, \(CL_t\), son los movimientos recurrentes hacia arriba y hacia abajo con respecto a los niveles de la tendencia.

Descomposición aditiva:

Para series de tiempo con variación estacional constante.

\[y = TR_t + SN_t + CL_t + IR_t\]

ClasificaciónPegel

Descomposición de las series en `R`:

estacional <- read.csv("Estacionalidad.csv", sep = ",", dec = ".", header = T)

Primero debemos convertir el objeto de la serie de tiempo a un objeto ts para que se pueda cargar en decompose() que en la función para descomponer la serie de tiempo.

Esto es muy común en la modelación de las series de tiempo, antes de aplicar los modelos, convertir los datos en ts.

Las funciones ts() ydecompose() son de la librería stats.

Con ts() se puede especificar la fecha inicial y final de la serie de tiempo con los siguientes argumentos: start = c(año,mes), end = c(año,mes). Para especificar la frecuencia de los datos se agrega el argumento: frequency =. Si los datos son mensuales se pone 12, si son trimestrales, 4, etc.

La serie de tiempo estacional no es una serie real, solo se creó para los ejemplos. En ts() no especificaremos las fechas de las serie de tiempo, pero si la frecuencia para poder utilizar la función decompose(), se tendrá el supuesto de que la serie de tiempo es mensual, por tanto, frequency = 12. Si se asume otra frecuencia el resultado de la descomposición cambia.

estacional <- ts(estacional, frequency = 12)

decompose <- decompose(estacional)
decompose

$x
         Jan        Feb        Mar        Apr        May        Jun        Jul
1.2026828  1.8367861  1.2442082  0.7727209  0.5337453 -0.6102938 -0.5144100
2.6251946  2.4515889  2.8351613  2.2859972  1.8694217  1.5721461  1.0502858
3.2992367  3.7647258  4.1327094  3.9925741  3.4241588  2.8354822  2.0184399
3.9628845  5.1106396  5.1782534  5.3047738  5.0001233  4.3337633  3.2865388
4.9317941  5.8472142  6.2735598  6.9872686  6.4809596  6.5183766  5.2941263
6.0252207  6.6477995  7.1865786  7.6562103  7.7373140  7.5709648  7.0182733
6.5818510  7.3234092  8.1061113  8.8865823  9.0500176  9.2761011  8.5709034
7.5651845  8.4569446  9.3495594  9.9424333 10.0839361 10.4694078  9.5882462
8.2572978  8.9481321  9.6600890 10.6113738
         Aug        Sep        Oct        Nov        Dec
-0.6384637 -0.5429922  0.4702575  1.4013552  2.0399015
0.5198622  0.5767464  0.8949620  2.0003338  2.5936841
2.0155806  1.7642253  2.2740441  2.7467055  3.3497802
3.2220106  2.9047779  3.3205185  3.4709205  4.0312092
5.1192112  4.4485744  4.6122909  4.9252277  4.8494827
6.5712279  6.2794672  5.7871986  5.6814357  6.3617022
7.8934253  7.4763065  6.9536320  6.9388675  7.3991301
9.4137737  8.8180279  8.5792719  8.2329555  8.3538300
9

$seasonal
          Jan         Feb         Mar         Apr         May         Jun
0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
0.07740675  0.61614510  0.99482020  1.17567569
          Jul         Aug         Sep         Oct         Nov         Dec
-0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011
-0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011
-0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011
-0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011
-0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011
-0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011
-0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011
-0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011
9

$trend
        Jan       Feb       Mar       Apr       May       Jun       Jul
      NA        NA        NA        NA        NA        NA 0.6588961
1.3864588 1.4999181 1.5948374 1.6591892 1.7018427 1.7498744 1.8010338
2.4640699 2.5667312 2.6785311 2.7854712 2.8740317 2.9366346 2.9957906
3.6411052 3.7442106 3.8420016 3.9331277 4.0069064 4.0654749 4.1342390
4.8565785 5.0192780 5.1626529 5.2808016 5.3952216 5.4899125 5.5695666
6.0779229 6.2102630 6.3470509 6.4722926 6.5527558 6.6472736 6.7334756
7.3083077 7.4280922 7.5330520 7.6315217 7.7325161 7.8281353 7.9123337
8.4673668 8.5731039 8.6923569 8.8159969 8.9376522 9.0313517 9.0999690
      NA        NA        NA        NA
        Aug       Sep       Oct       Nov       Dec
0.7437842 0.8356907 0.9650336 1.0837400 1.2303282
1.8838329 1.9926114 2.1177833 2.2536714 2.3710911
3.0795223 3.1791664 3.2774057 3.3977458 3.5258394
4.2053008 4.2816292 4.3973709 4.5291764 4.6819035
5.6484838 5.7198840 5.7857990 5.8660197 5.9622256
6.7848190 6.8512832 6.9408626 7.0468241 7.1725674
8.0005365 8.0995775 8.1953816 8.2824554 8.3752564
9.1492732 9.1826780 9.2234893        NA        NA
9

$random
           Jan          Feb          Mar          Apr          May          Jun
         NA           NA           NA           NA           NA           NA
1.161329022  0.335525733  0.245503715 -0.548867753 -0.717748884 -0.831996319
0.757760120  0.581849506  0.459358113  0.031427296 -0.335200898 -0.755420346
0.244372532  0.750283856  0.341431608  0.195970451  0.107888936 -0.385979544
-0.002191147  0.211791060  0.116086735  0.530791336  0.200410123  0.374196143
-0.130108939 -0.178608610 -0.155292559  0.008242036  0.299230271  0.269423191
-0.803863475 -0.720828054 -0.421760910  0.079384887  0.432173539  0.793697806
-0.979589108 -0.732304486 -0.337617697 -0.049239248  0.260955917  0.783788073
         NA           NA           NA           NA
           Jul          Aug          Sep          Oct          Nov          Dec
-0.813806568 -0.674495321 -0.291122569  0.541979656  1.109400347  1.229863426
-0.391248352 -0.656218086 -0.328304645 -0.186065484  0.538447569  0.642883056
-0.617851071 -0.356189069 -0.327380623  0.033394272  0.140744779  0.244230887
-0.488200632 -0.275537652 -0.289290940 -0.040096647 -0.266470806 -0.230404211
0.084059248  0.178480051 -0.183749152 -0.136752215 -0.149006843 -0.692452745
0.644297206  0.494161512  0.515744329 -0.116908209 -0.573603260 -0.390575166
1.018069349  0.600641390  0.464289365 -0.204993793 -0.551802782 -0.555836242
0.847776825  0.972253180  0.722910239  0.392538426           NA           NA
9

$figure
 [1]  0.07740675  0.61614510  0.99482020  1.17567569  0.88532792  0.65426799
 [7] -0.35949957 -0.70775262 -1.08756040 -1.03675583 -0.79178512 -0.42029011

$type
[1] "additive"

attr(,"class")
[1] "decomposed.ts"

plot(decompose)

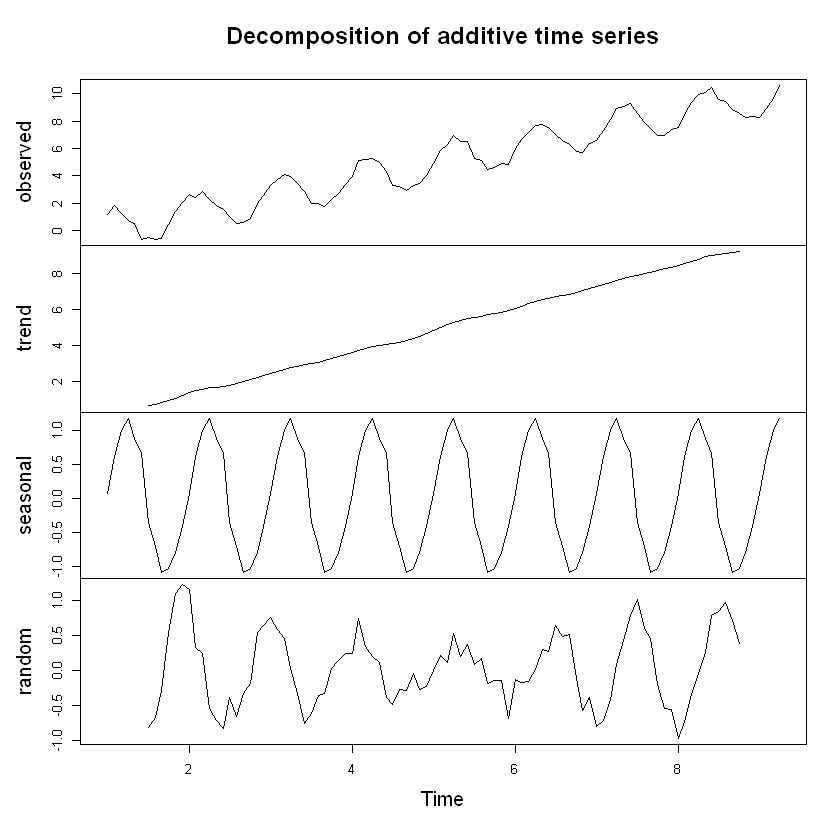
estacional2 <- read.csv("Estacionalidad2.csv", sep = ",", dec = ".", header = T)
estacional2 <- estacional2[,2]
estacional2 <- ts(estacional2, frequency = 12)
plot(decompose(estacional2))

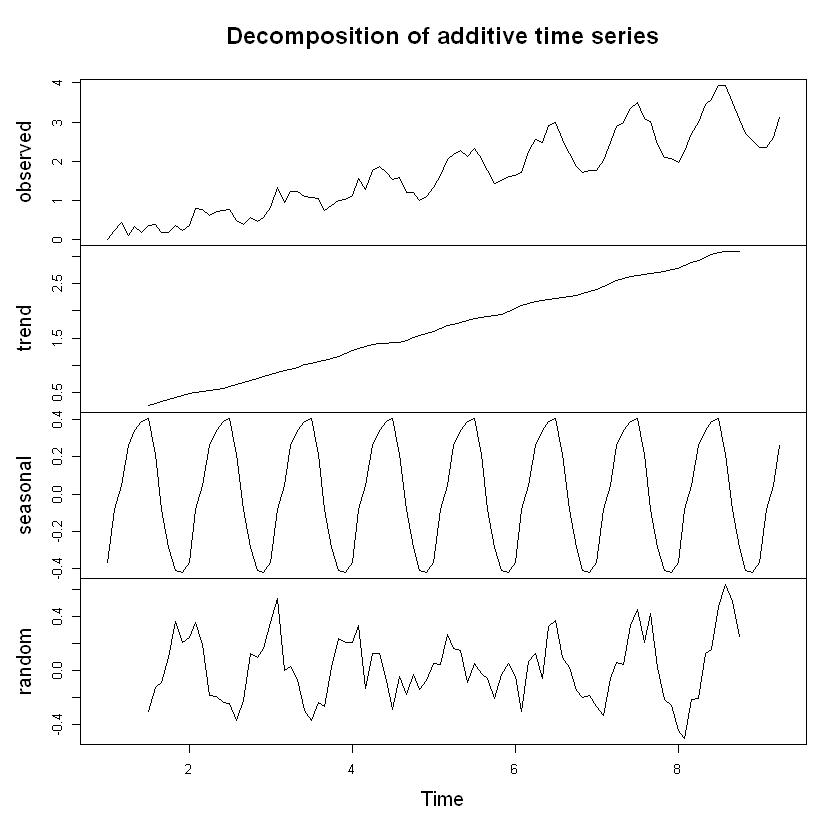
tendencia <- read.csv("Tendencia.csv", sep = ",", dec = ".", header = T)
tendencia <- tendencia[,2]
tendencia <- ts(tendencia, frequency = 12)
plot(decompose(tendencia))

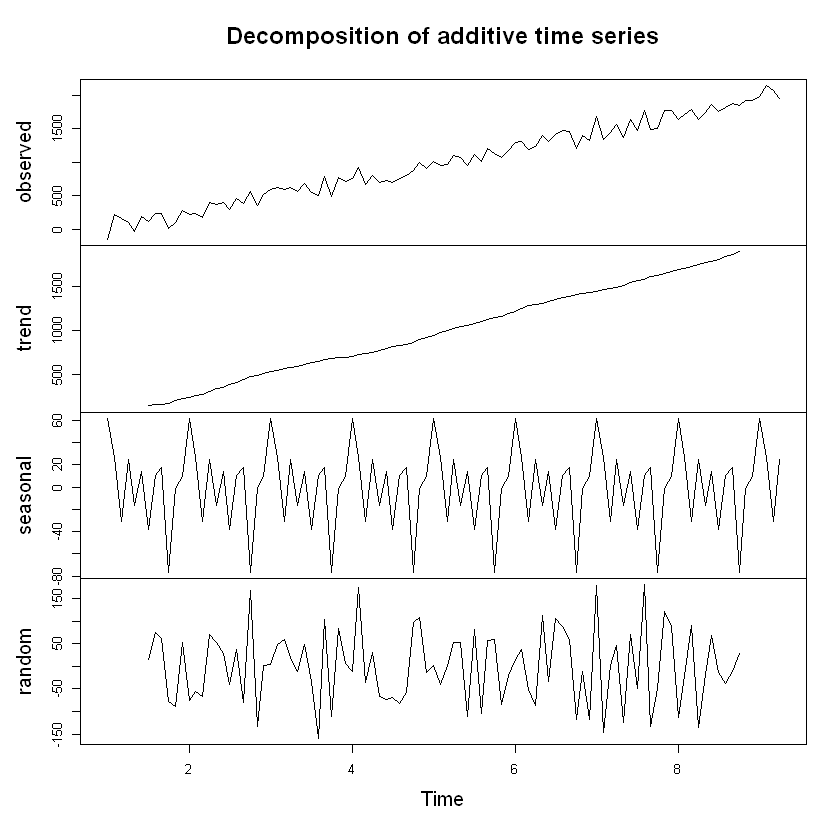
ejemplo3 <- read.csv("ejemplo3.csv", sep = ",", dec = ".", header = T)
ejemplo3 <- ejemplo3[,2]
ejemplo3 <- ts(ejemplo3, frequency = 12)
plot(decompose(ejemplo3))

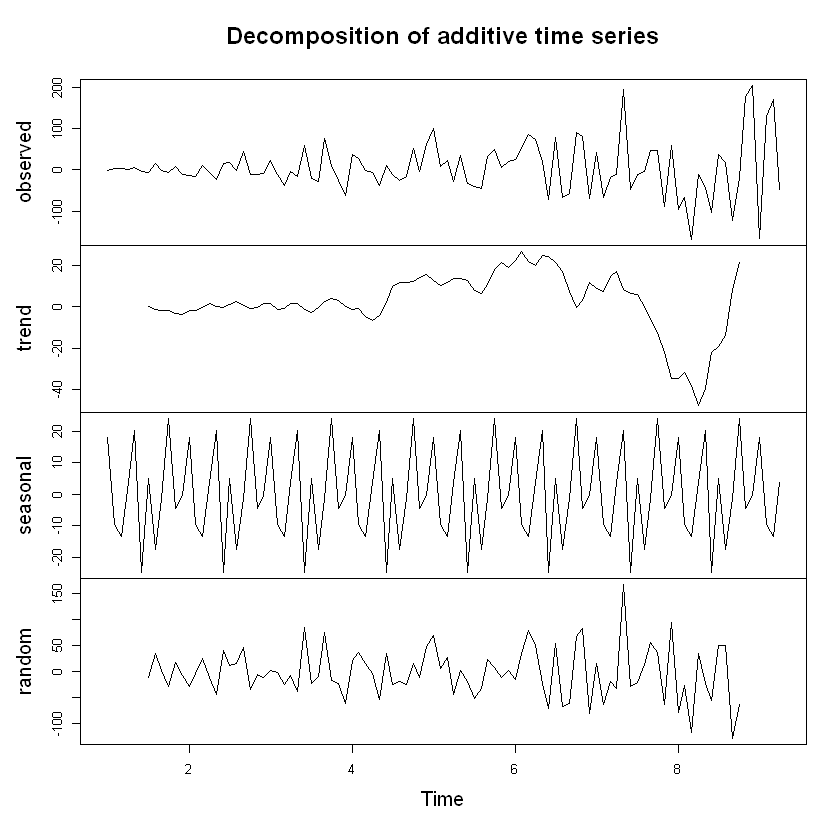
ruidoblanco <- read.csv("ruidoblanco.csv", sep = ",", dec = ".", header = T)
ruidoblanco <- ruidoblanco[,2]
ruidoblanco <- ts(ruidoblanco, frequency = 12)
plot(decompose(ruidoblanco))

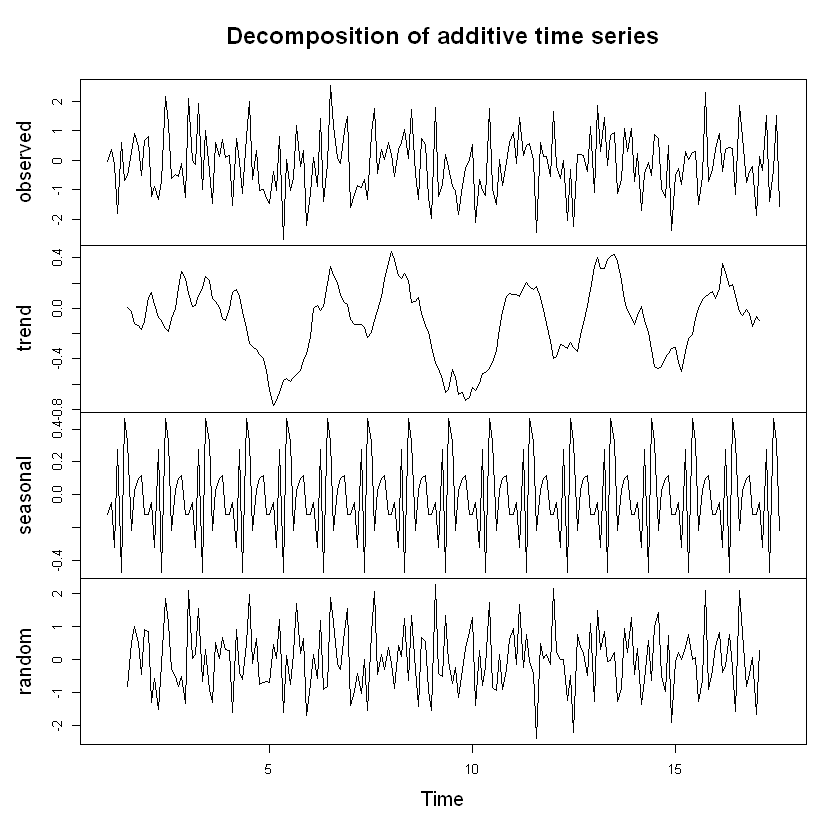
Estacionariedad:

La estacionariedad es una característica de algunas series de tiempo. Toda serie de tiempo tiene una tendencia y una oscilación alrededor de la tendencia, una serie de tiempo es estacionaria si la tendencia siempre es la misma a los largo del horizonte de tiempo de análisis y además, las variaciones de la serie de tiempo oscilan alrededor de esta tendencia. Lo anterior significa que las series estacionarias tienen una media constante y una varianza constante. Se dice que tiene un equilibrio estadístico con propiedades probabilísticas que no cambian a través del tiempo.

Identifique cuáles de los siguientes ejemplos de series temporales tienen la condición de estacionariedad y cuáles no.

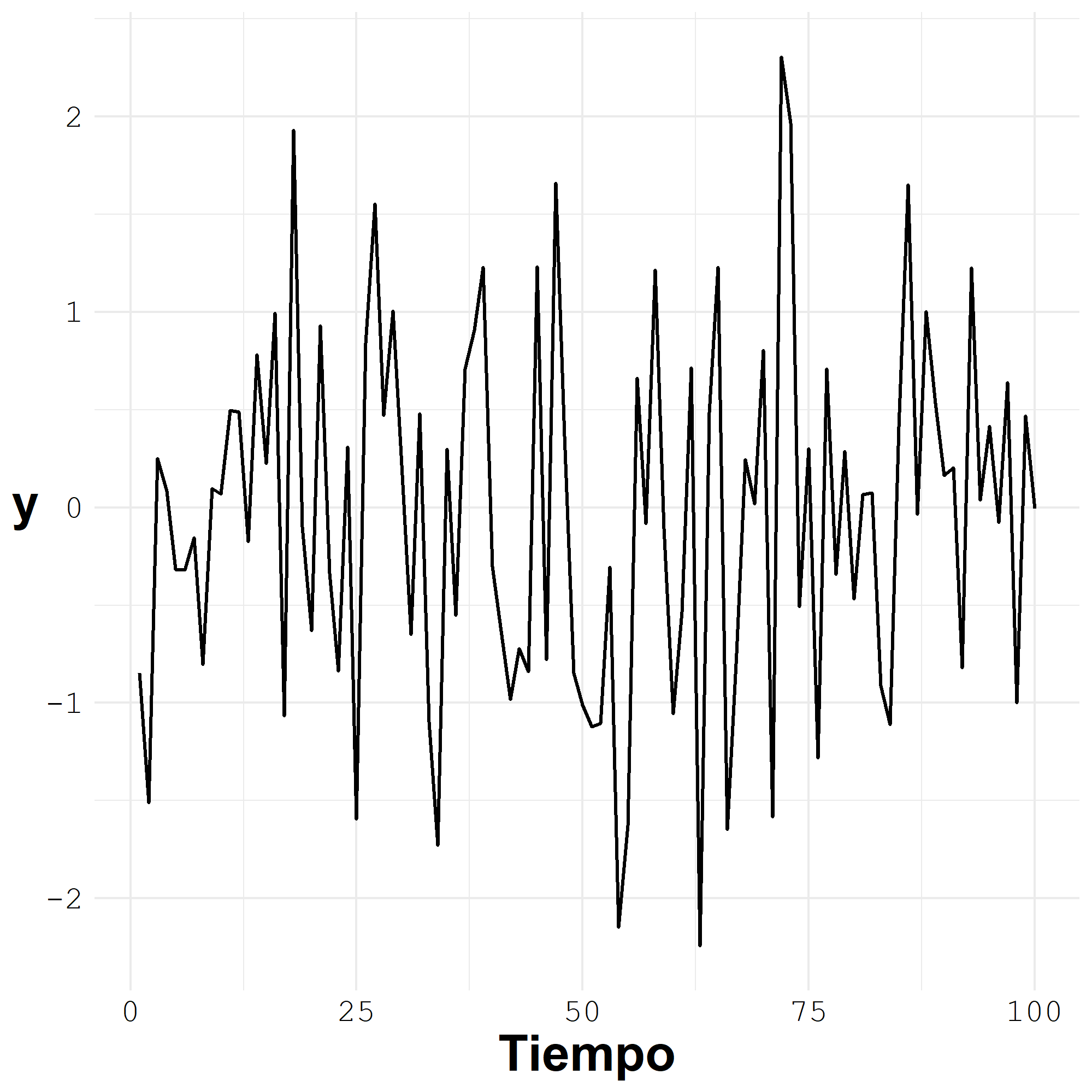
EjemploWhiteNoise

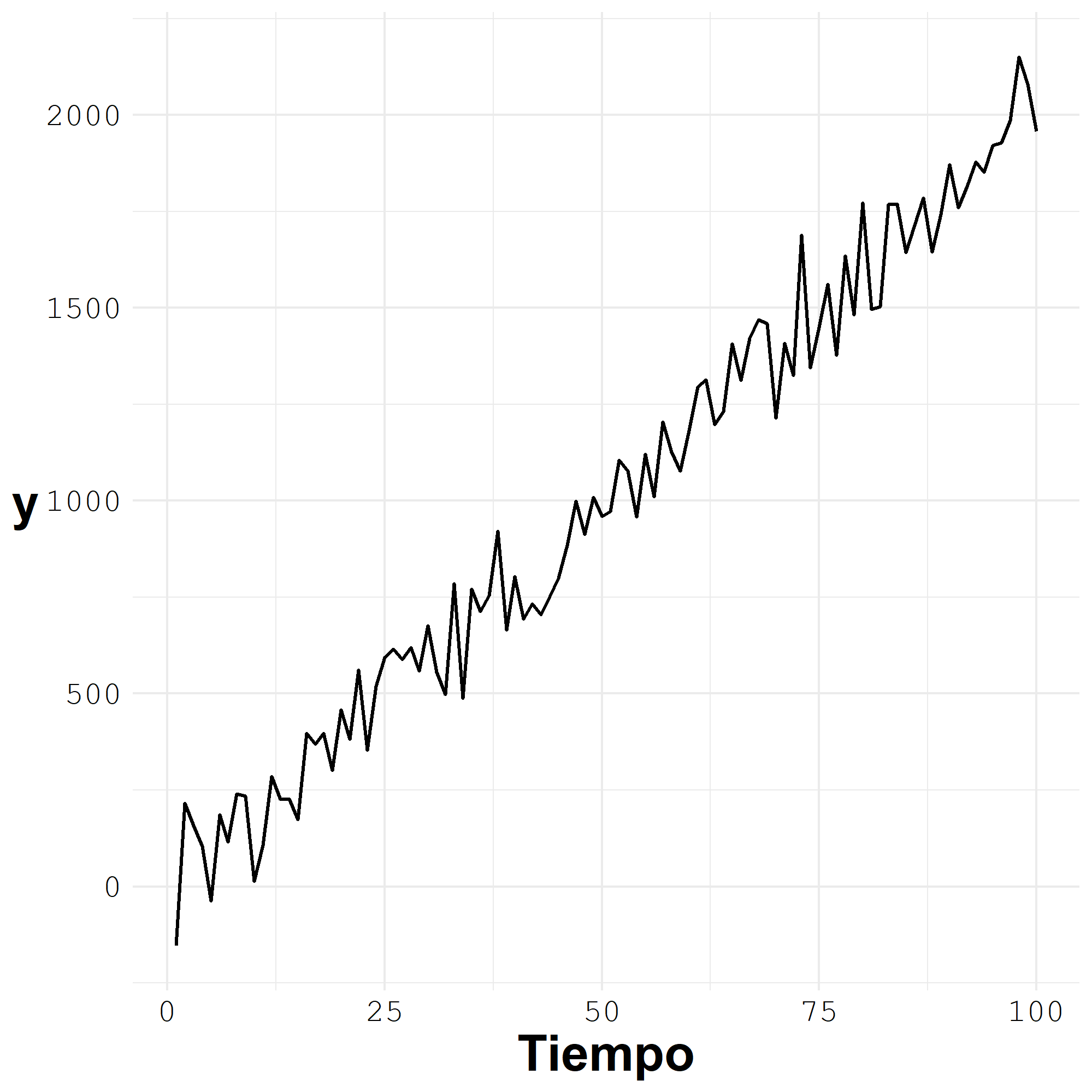
EjemploTendencia

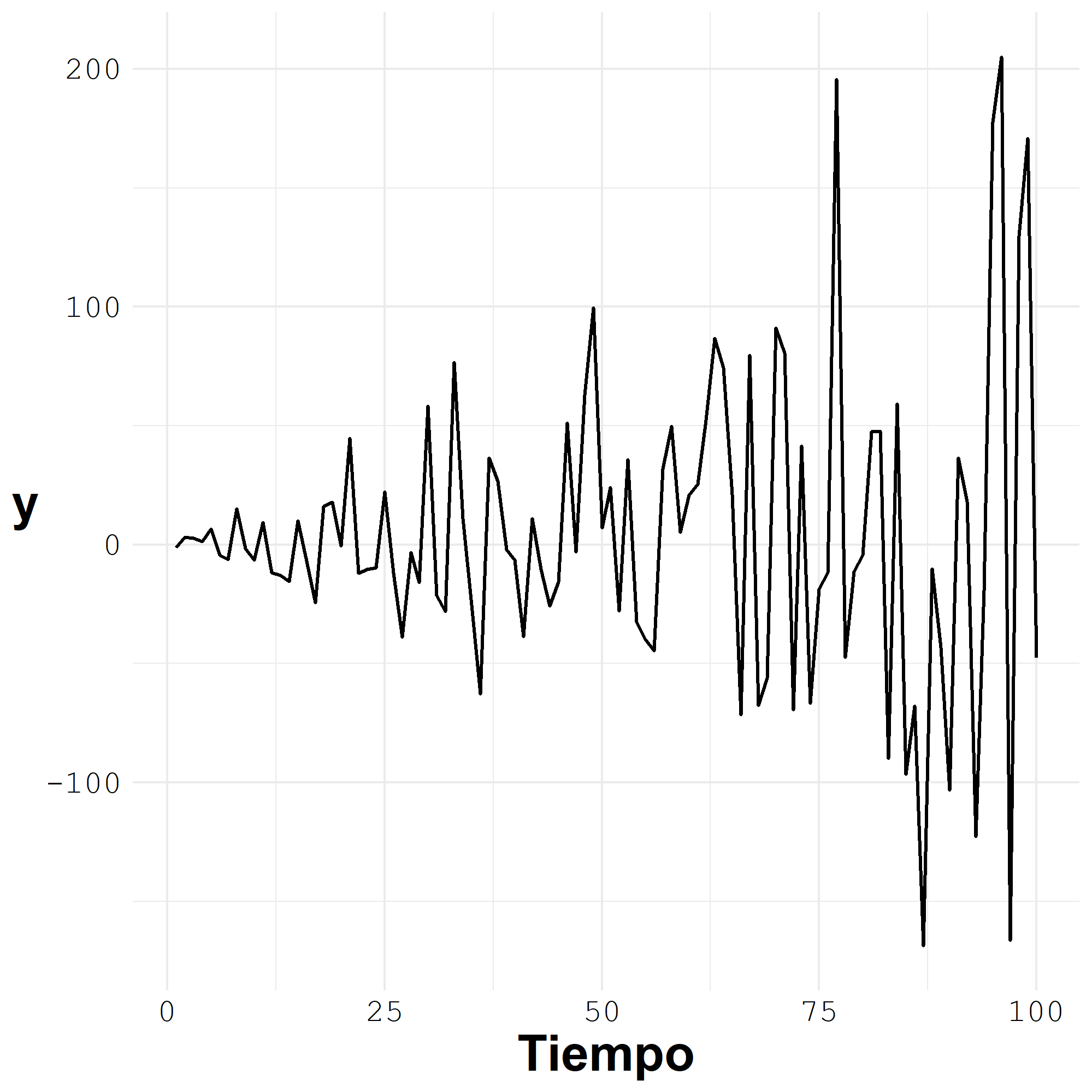
Ejemplo3

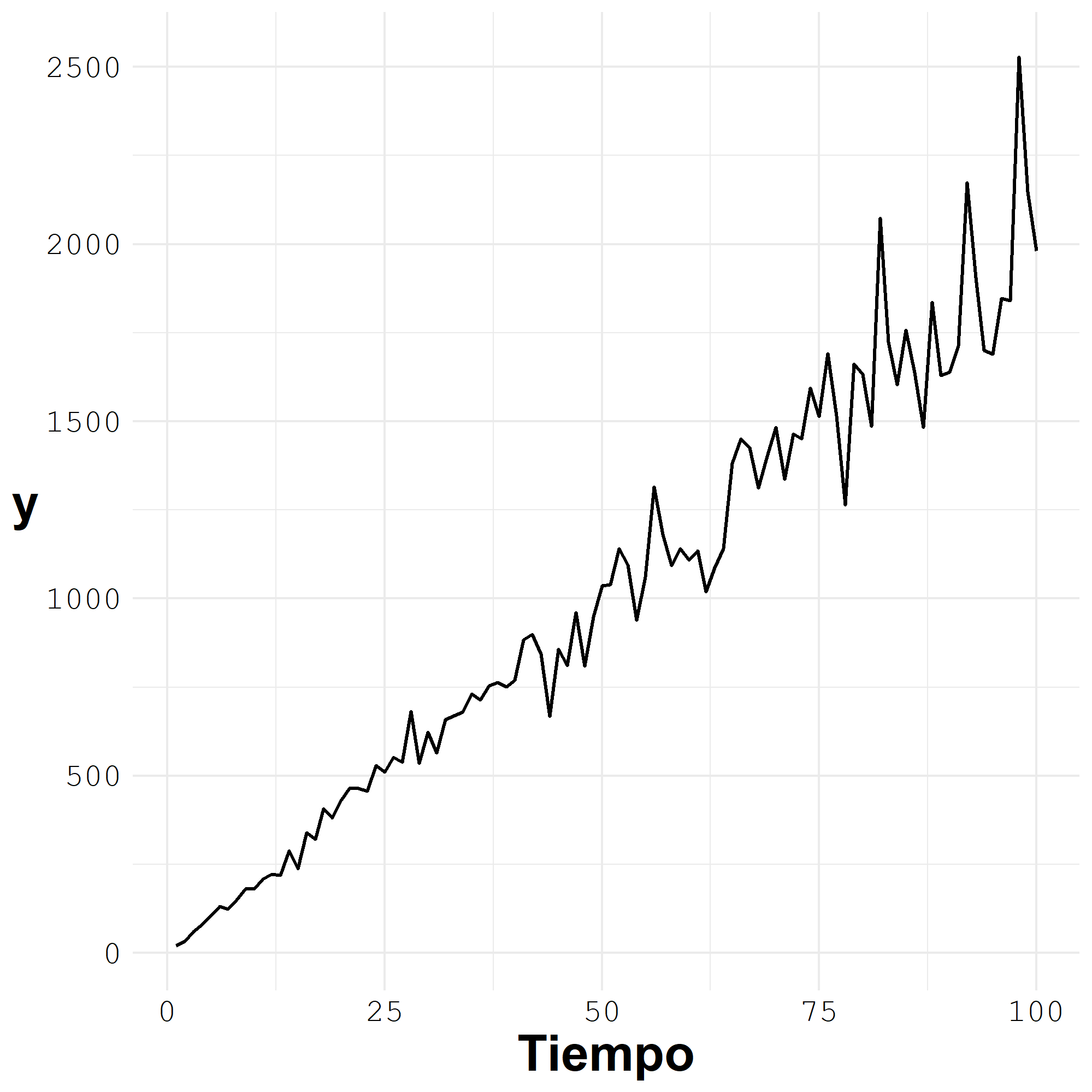
Ejemplo4

Estacionalidad

Estacionalidad2

Media y varianza:

Los gráficos de series de tiempo tienen en el eje \(X\) la variable tiempo \(t\) y en el eje \(y\) el valor que toma la serie, así que \(y\) depende de \(t\) y se denota \(y_t\). \(y_t\) son los valores de la serie de tiempo original; sin embargo, como se verá más adelante, los valores originales pueden ser transformados y se obtendrá otra serie temporal. Esta es una condición para poder aplicar los modelos convencionales de series de tiempo. De esta manera, utilizaremos la notación \(z_t\) para referirnos ya sea a la serie de tiempo original o a la transformada.

Si \(z_t\) es la variable que estamos trabajando, podemos calcular la media \(\overline{z}\) de la siguiente manera:

\[\overline{z} = \frac{1}{N}\sum_{t=1}^N{z_t}\]

Donde \(N\) es la cantidad total de valores que tenemos de la serie de tiempo. Si tenemos \(N=100\) precios de una acción (100 valores para \(z_t\)), tenemos 100 puntos en el tiempo \(t\). El intervalo entre cada punto en el tiempo es el mismo.

La forma de medir el grado de oscilación de las observaciones alrededor de la media es por medio de la varianza \(\sigma_z^2\):

\[\sigma_z^2=\frac{1}{N}\sum_{t=1}^N{(z_t-\overline{z})^2}\]

Procesos estocásticos:

Un fenómeno estadístico que evoluciona en el tiempo de acuerdo con leyes probabilísticas se denomina proceso estocástico. A veces se denomina solo proceso.

Existe una clase de procesos estocásticos llamados procesos estacionarios. Un proceso estrictamente estacionario es aquel donde las propiedades estadísticas no cambian en el tiempo. Para cualquier intervalo de tiempo, la distribución de probabilidad es invariante.

El supuesto de estacionariedad implica que una serie de tiempo \(z_t\) tiene una distribución de probabilidad \(p(z_t)\) invariante para todos los intervalos de tiempo y puede ser reescrita como \(p(z)\). Así que el proceso estocástico tiene media constante:

\[\mu = E[z_t] = \int_{-\infty}^{\infty}{zp(z)dz}\]

La media en el proceso estocástico puede ser estimada como \(\overline{z}= \frac{1}{N}\sum_{t=1}^N{z_t}\). Esta media es el nivel de fluctuación de las observaciones.

La varianza constante es:

\[\sigma_z^2=E[(z_t-\mu)^2]=\int_{-\infty}^{\infty}{(z-\mu)^2p(z)dz}\]

La varianza del proceso estocástico puede ser estimada como \(\sigma_z^2=\frac{1}{N}\sum_{t=1}^N{(z_t-\overline{z})^2}\).

El supuesto de estacionariedad también implica que la distribución de probabilidad conjunta \(p(z_{t_1},z_{t_2})\) es la misma para todos los puntos en el tiempo \(t_1\) y \(t_2\). Esto indica que la covarianza entre los valores \(z_t\) y \(z_{t+k}\) separados por intervalo de tiempo \(k\), o por un rezago (lag) \(k\), debería ser la misma para todos los intervalos de tiempo.

Para un proceso estacionario, la varianza \(\sigma_z^2=\gamma_0\) es la misma en el tiempo \(𝑡 + 𝑘\) como en el tiempo \(𝑡\). Por lo tanto, la autocorrelación en el rezago \(𝑘\), es decir, la correlación entre \(z_t\) y \(z_{t+k}\) es:

\[\rho_k = \frac{\gamma_k}{\gamma_0}\]

Lo anterior implica que \(\rho_0=1\), lo que es obvio.

Más adelante se explicará con mayor profundidad la autocorrelación.

Ruido blanco:

El ruido blanco (white noise) es un ejemplo de un proceso estacionario y es una secuencia de variables aleatorias independientes e idénticamente distribuidas denotadas \(a_1, a_2, a_3, \dotso, a_t\) que es común asumir que tienen media cero y varianza constante \(\sigma_a^2\). Este proceso es estrictamente estacionario.

La independencia implica que los rezagos de \(a_t\) están incorrelacionados y tienen la siguiente función de autocovarianza:

Si \(k=0\): \(\gamma_k=\sigma_a^2\)
Si \(k\neq0\): \(\gamma_k=0\)

Los procesos de ruido blanco tienen un papel muy importante en la construcción de los modelos para series de tiempo.

El ruido blanco es una secuencia de datos aleatorios donde cada valor tiene un período de tiempo asociado y la serie de tiempo tiene un comportamiento aleatorio y no se puede proyectar el futuro.

Un ruido blanco es una serie temporal que no tiene un patrón y por lo cual no se puede predecir el futuro.

Para que la serie de tiempo sea Ruido Blanco debe tener:

Media constante.
Varianza constante.
Sin autocorrelaciones en ningún período (no tiene estacionalidad).

El proceso de ruido blanco se puede resumir con la siguiente expresión:

\[a_t \sim^{iid}N(0,\sigma^2)\]

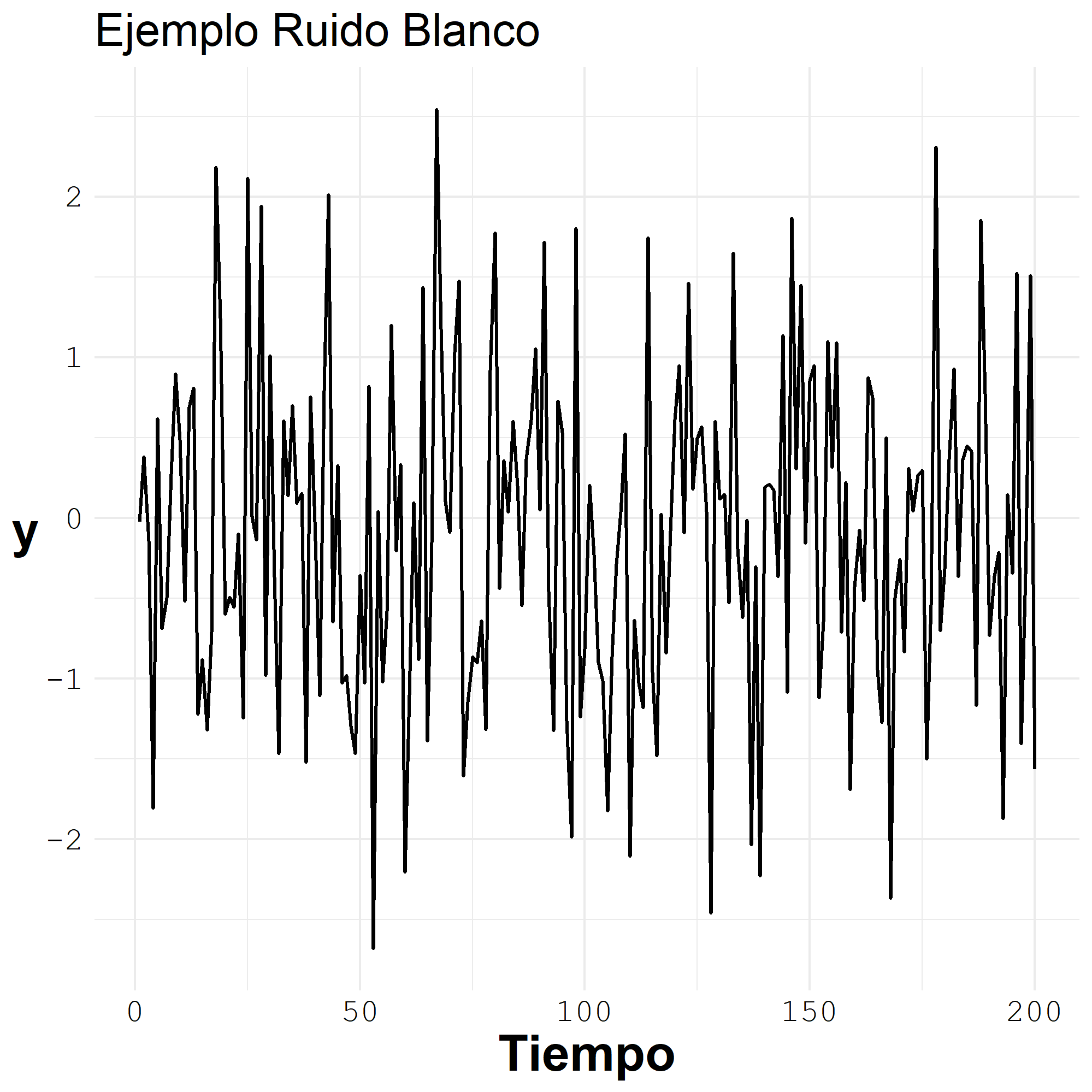
RuidoBlanco