Modelos Autorregresivos - AR

Una serie de tiempo puede ser lineal si puede ser representada como:

\[z_t = \mu+\sum_{i=0}^{\infty}{\Psi_i a_{t-i}}\]

Donde \(\mu\) es la media de \(z_t\), \(\Psi_0=1\) y \(a_t\) es una secuencia de variables aleatorias independientes e idénticamente distribuidas con media cero (podría ser un ruido blanco).

\(a_t\) también es llamado las innovaciones o shock en el período \(t\) y representa la nueva información en el período \(t\) de la serie de tiempo.

La serie de tiempo \(z_t\) depende de los coeficientes \(\Psi_i\), que son llamados los pesos de \(z_t\).

AR(1):

Los modelos autorregresivos (Autoregressive Models) de orden 1 - AR(1) - se describen de la siguiente manera:

\[z_t = \phi_0 + \phi_1 z_{t-1} + a_t\]

Donde \(a_t\) se asume que es una serie ruido blanco con media cero y varianza constante. Este modelo es de la forma de una regresión lineal simple en que \(z_t\) es la variable dependiente y \(z_{t-1}\) es la variable explicativa.

\[E(z_t|z_{t-1}) = \phi_0 + \phi_1 z_{t-1}\]

\[Var(z_t|z_{t-1}) = Var(a_t) = \sigma_a^2\]

Esto es que, dado el valor pasado $z_{t-1} $, el actual valor \(z_t\) está centrado en \(\phi_0 + \phi_1 z_{t-1}\) con desviación estándar \(\sigma_a^2\).

Propiedades del modelo AR(1):

Podemos determinar la media, varianza y las autocorrelaciones del modelo AR (1).

Partiendo de la ecuación del AR(1):

\[z_t = \phi_0 + \phi_1 z_{t-1} + a_t\]

Sabemos que \(E(a_t)=0\) porque se supone que \(a_t\) es una secuencia de variables aleatorias independientes e idénticamente distribuidas con media cero (ruido blanco), entonces:

\[E(z_t) = \phi_0 + \phi_1 E(z_{t-1})\]

Bajo la condición de estacionariedad, \(E(z_t) = E(z_{t-1})= \mu\) porque la media es constante, por tanto:

\[\mu = \phi_0 + \phi_1 \mu\]

\[\mu = \frac{\phi_0}{1-\phi_1}\]

Lo anterior tiene dos implicaciones:

1. La media de \(z_t\) existe si \(\phi_1 \neq 1\).

2. La media de \(z_t\) es cero si \(\phi_0 = 0\).

Despejando \(\phi_0\) tenemos:

\[\phi_0 = (1 - \phi_1)\mu\]

Podemos reescribir el modelo AR(1) reemplazando \(\phi_0\) en \(z_t\):

\[z_t - \mu = \phi_1(z_{t-1}-\mu) + a_t\]

AR(p):

De forma generalizada, los modelos autorregresivo de orden \(p\) - AR(p) se describen:

\[z_t = \phi_0 + \phi_1 z_{t-1}+ \phi_2 z_{t-2}+...+ \phi_p z_{p-1} + a_t\]

Donde \(p\) es un entero positivo. Este modelo dice que las \(p\) valores pasados (rezagos) de \(z_{t-i}\) \((i= 1,2,...,p)\) determinan \(z_t\). Este modelo es de la misma forma que un modelo de regresión lineal múltiple con los rezagos como variables explicativas.

\[E(z_t) = \frac{\phi_0}{1-\phi_1-...-\phi_p}\]

Estimación de los parámetros:

El modelo AR(p) se especifica de la siguiente forma:

\[z_t = \phi_0 + \phi_1 z_{t-1}+ \phi_2 z_{t-2}+...+ \phi_p z_{p-1} + a_t\]

Esta es la forma de una regresión lineal múltiple y los parámetros pueden ser estimados por el método de mínimos cuadrados. Por tanto, el modelo estimado sería:

\[\hat{z_t} = \hat{\phi_0} + \hat{\phi_1} z_{t-1}+ \hat{\phi_2} z_{t-2}+...+ \hat{\phi_p} z_{p-1}\]

El residual (residual series) es:

\[\hat{a_t} = z_t - \hat{z_t}\]

La varianza del residual es:

\[\hat{\sigma_a^2} = \frac{\sum_{t=p+1}^n{\hat{a_t^2}}}{n-2p-1}\]

Identificación del orden p de AR:

Se pueden usar dos enfoques para determinar el orden \(p\) del modelo AR: Usar PACF o algún el criterio de información (AIC o BIC).

• Con PACF: se selecciona el orden con el último lag de los valores más grandes.

• Con AIC: se selecciona el orden que tenga el menor valor del AIC.

Partial Autocorrelation Function (PACF):

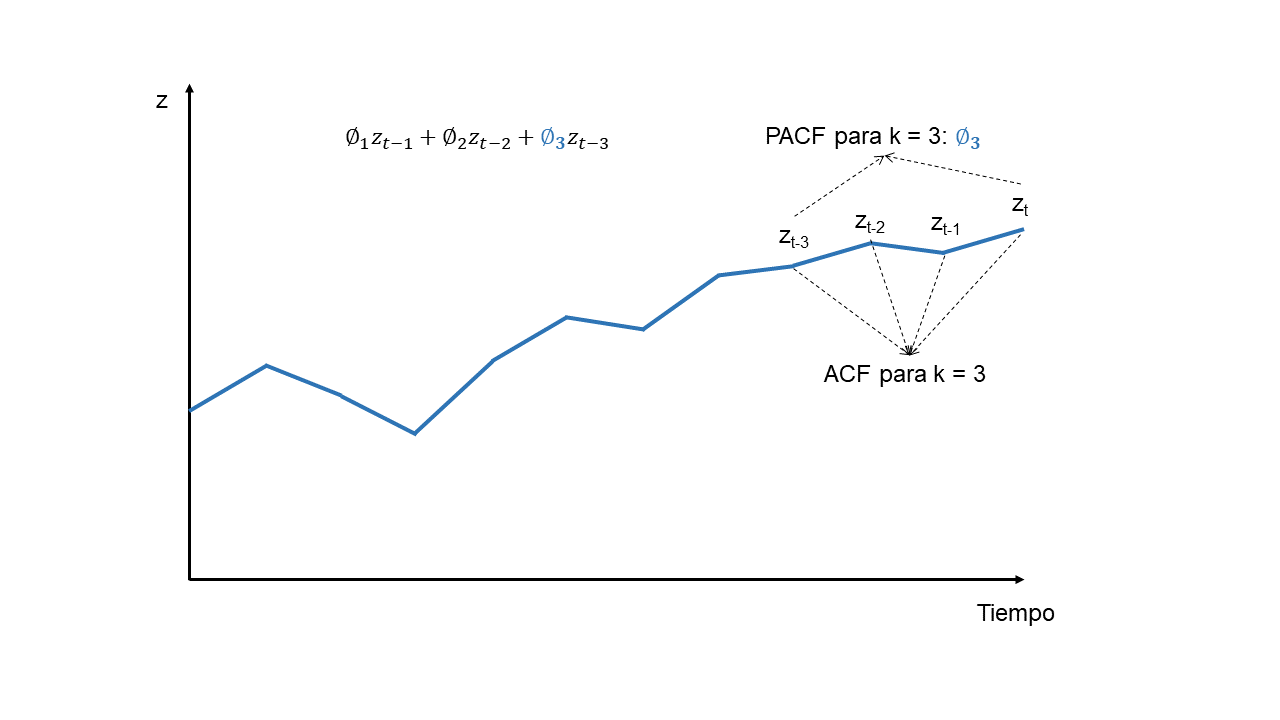
La ACF mide la relación lineal entre \(z_t\) y \(z_{t-k}\), pero esta medida está relacionada con el encadenamiento que hay entre \(z_t\) y \(z_{t-k}\) a través de las variables \(z_{t-1}, \dotso , z_{t-k+1}\). En cambio, la PACF (Partial Autocorrelation Function) mide la relación entre \(z_t\) y \(z_{t-k}\) sin el efecto de las variables intermedias.

PACFvsACF

El coeficiente de autocorrelación parcial entre \(z_t\) y \(z_{t-k}\) se denota como \(\rho_{kk}\) y es proporcional a la correlación entre \(z_t\) y \(z_{t-k}\) menos la parte que puede ser explicada por las variables intermedias.

La PACF para el rezago \(k\) es el último coeficiente de un modelo AR(k).

La PACF para \(k=0\) es uno y para \(k=1\) es igual al valor de la ACF porque no hay variables intermedias.

A diferencia que el ACF, la PACF tiene como hipótesis nula que la serie es realmente un AR(p). Se buscar con la PACF el orden \(p\) con el rezago con el valor que supere la franja de decisión y que los valores de la PACF para el rezago superiores \(p\) sean cero.

Al igual que en ACF, se usa el límite de \(2\pm se[\rho_{kk}]\), pero para la PACF se busca el orden \(p\) para los modelos AR(p). Los valores de \(\rho_k\) mayores a \(2\pm se[\rho_{kk}]\) se concluyen que son mayores que cero.

Si \(\rho_{kk}\) está por fuera del rango \(\frac{2}{\sqrt{(N)}}\), la serie de tiempo se puede modelar como un AR(p).

Función pacf de R:

Para calcular el PACF y graficarlo usamos en R la función pacf() de la librería tseries.

estacional <- read.csv("Estacionalidad.csv", sep = ",", dec = ".", header = T)
estacional2 <- read.csv("Estacionalidad2.csv", sep = ",", dec = ".", header = T)
tendencia <- read.csv("Tendencia.csv", sep = ",", dec = ".", header = T)
ruidoblanco <- read.csv("ruidoblanco.csv", sep = ",", dec = ".", header = T)

library(ggplot2)

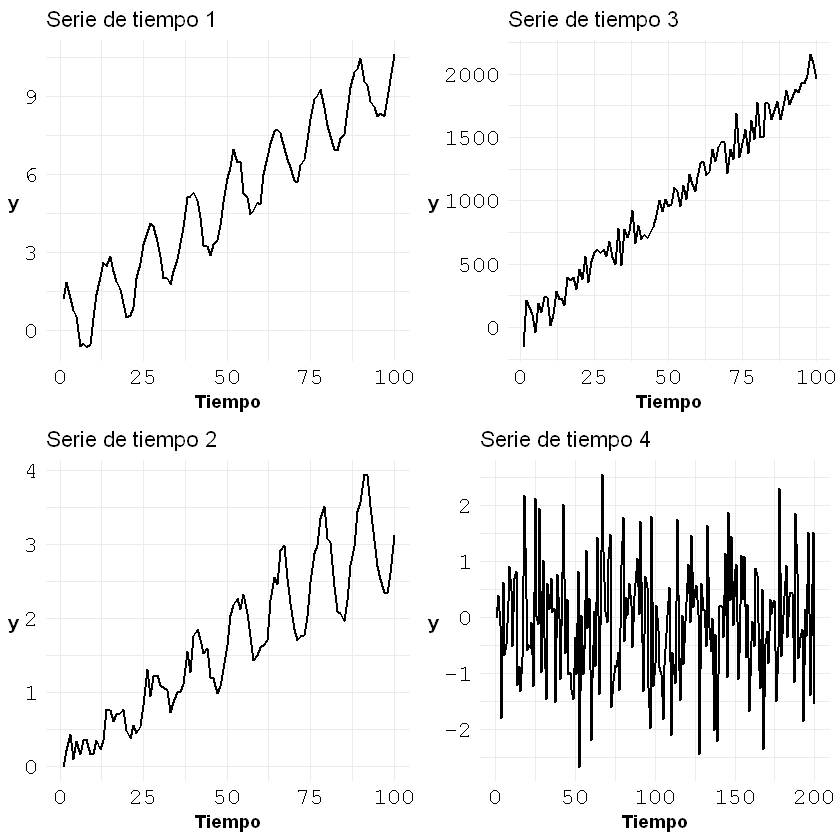
p1 <- ggplot()+geom_line(aes(x = c(1:nrow(estacional)), y = estacional[,1]), size = 0.7)+
        theme_minimal() +
        labs(title = "Serie de tiempo 1", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

p2 <- ggplot()+geom_line(aes(x = c(1:nrow(estacional2)), y = estacional2[,2]), size = 0.7)+
        theme_minimal() +
        labs(title = "Serie de tiempo 2", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

p3 <- ggplot()+geom_line(aes(x = c(1:nrow(tendencia)), y = tendencia[,2]), size = 0.7)+
        theme_minimal() +
        labs(title = "Serie de tiempo 3", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

p4 <- ggplot()+geom_line(aes(x = c(1:nrow(ruidoblanco)), y = ruidoblanco[,2]), size = 0.7)+
        theme_minimal() +
        labs(title = "Serie de tiempo 4", x = "Tiempo", y = "y")+
        theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
              axis.title.x = element_text(face = "bold", colour = "black", size = rel(1)),
              axis.title.y = element_text(face = "bold", colour = "black", size = rel(1), angle = 0,vjust = 0.5))

library(gridExtra)

Warning message:
"package 'gridExtra' was built under R version 4.1.3"

grid.arrange(p1, p2, p3, p4, ncol = 2,
             layout_matrix = cbind(c(1,2), c(3,4)))

layout(matrix(c(1:4), 2,2))
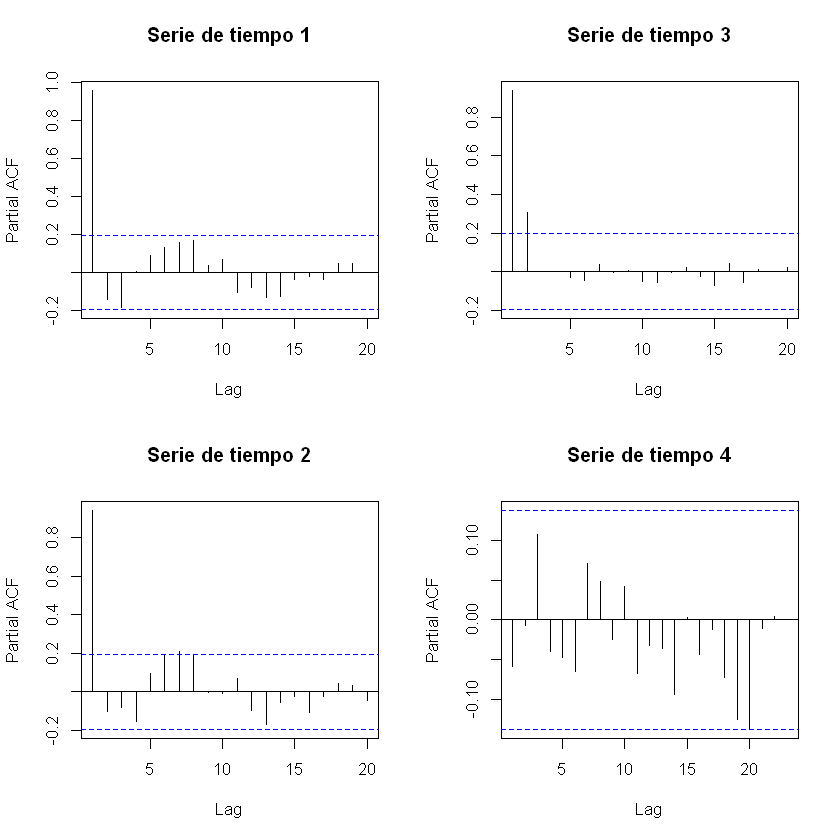
pacf(estacional[,1], main = "Serie de tiempo 1")
pacf(estacional2[,2], , main = "Serie de tiempo 2")
pacf(tendencia[,2], , main = "Serie de tiempo 3")
pacf(ruidoblanco[,2], , main = "Serie de tiempo 4")
#layout.show(2) # Muestra las dos particiones

Ajuste modelo AR en R:

Instalar la librería forecast para usar la función arima(). Esta función se aplica a series de tiempo univariadas.

install.packages("forecast")

library(forecast)

Warning message:
"package 'forecast' was built under R version 4.1.3"
Registered S3 method overwritten by 'quantmod':
  method            from
  as.zoo.data.frame zoo

arima(serie de tiempo, orde = c(p, 0, 0)): Para los modelos AR(p). El orden de \(p\) se determina con la PACF.

Ejemplo 1: serie estacional

p1

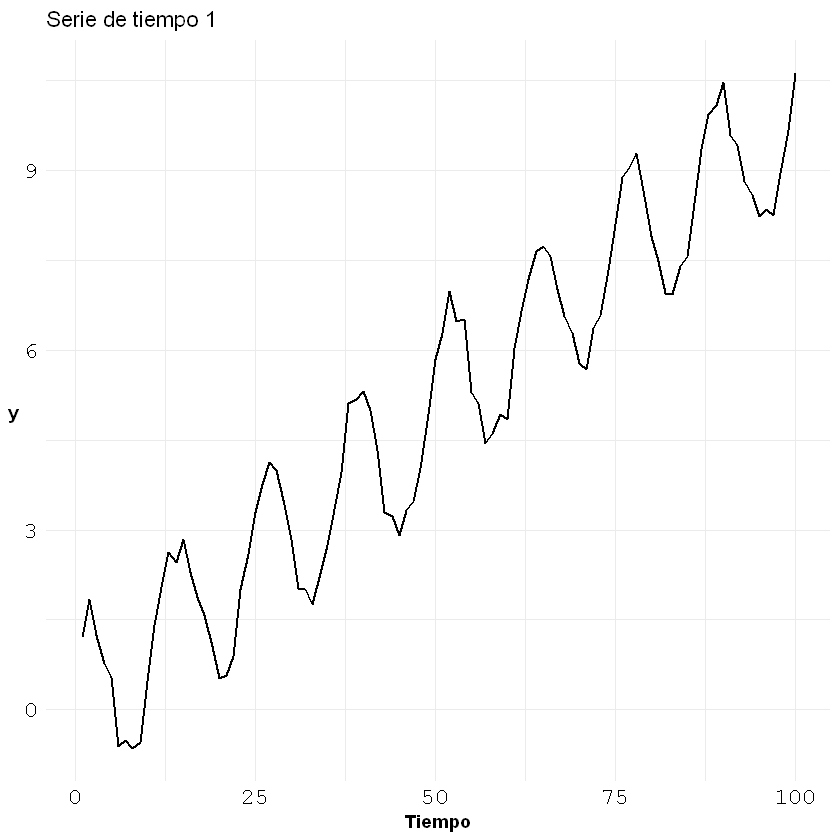
pacf(estacional[,1], main = "Serie de tiempo 1")

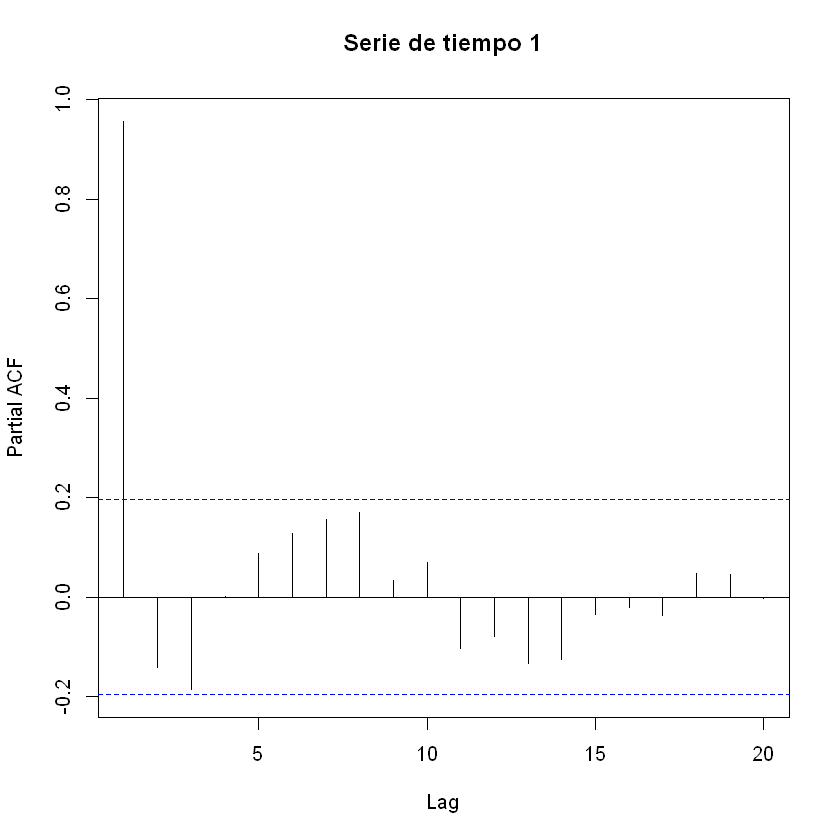
El orden es \(p=1\) porque es el único significativo. Está por fuera de las líneas azules (está por fuera del rango \(\frac{2}{\sqrt{(N)}}\)).

arima(estacional[,1], order = c(1, 0, 0))

Call:
arima(x = estacional[, 1], order = c(1, 0, 0))

Coefficients:
         ar1  intercept
      0.9895     5.5923
s.e.  0.0118     3.2046

sigma^2 estimated as 0.3253:  log likelihood = -87.68,  aic = 181.36

El modelo estimado sería:

\[\hat{z_t} = \hat{\phi_1} z_{t-1}\]

\[\hat{z_t} = 0,9895 z_{t-1}\]

El primer rezago es muy importante para modelar la serie de tiempo porque tiene un peso de 0,9895. La serie de tiempo depende de su historia.

Ejemplo 2: serie estacional, varianza no cosntante

p2

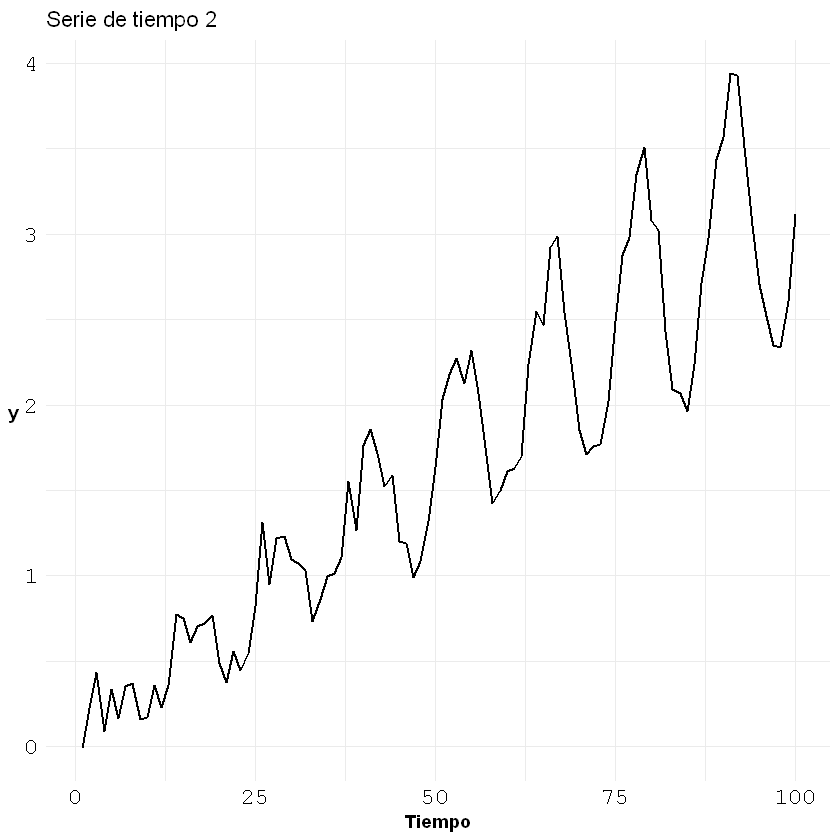
pacf(estacional2[,2], main = "Serie de tiempo 2")

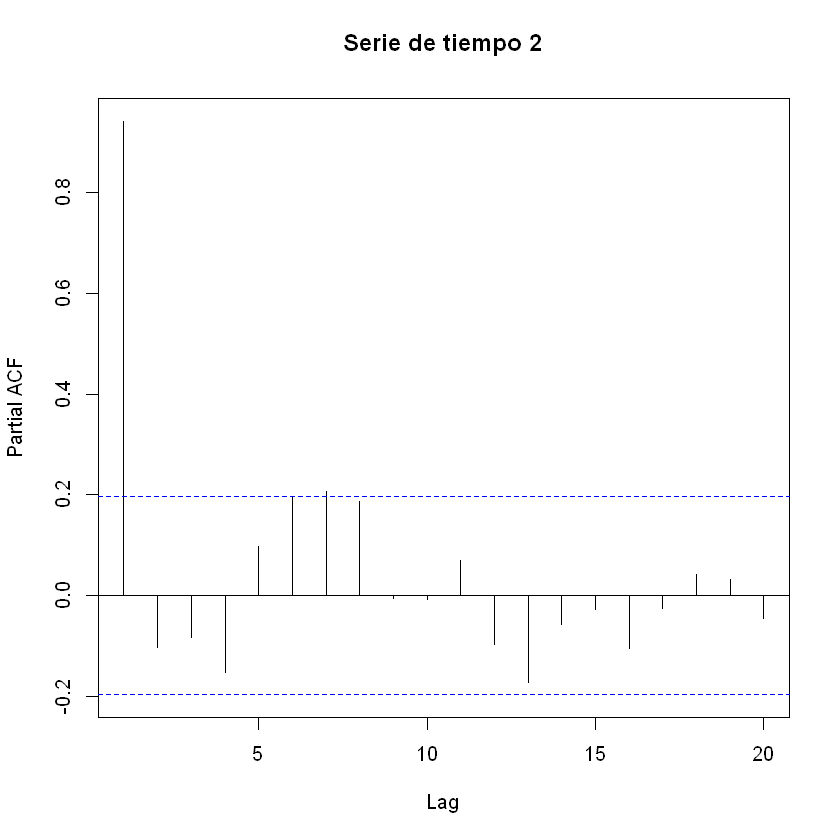
AR(1):

arima(estacional2[,2], order = c(1, 0, 0))

Call:
arima(x = estacional2[, 2], order = c(1, 0, 0))

Coefficients:
         ar1  intercept
      0.9749     1.6177
s.e.  0.0215     0.7873

sigma^2 estimated as 0.06952:  log likelihood = -10.09,  aic = 26.17

Ejemplo 3: serie con tendencia, varianza constante

p3

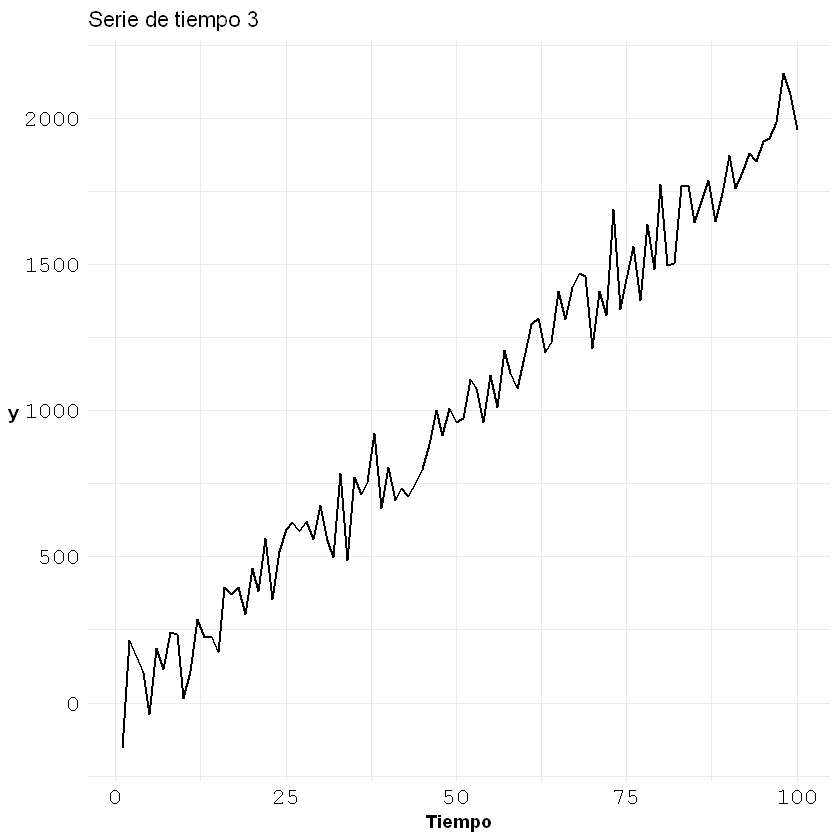
pacf(tendencia[,2], main = "Serie de tiempo 3")

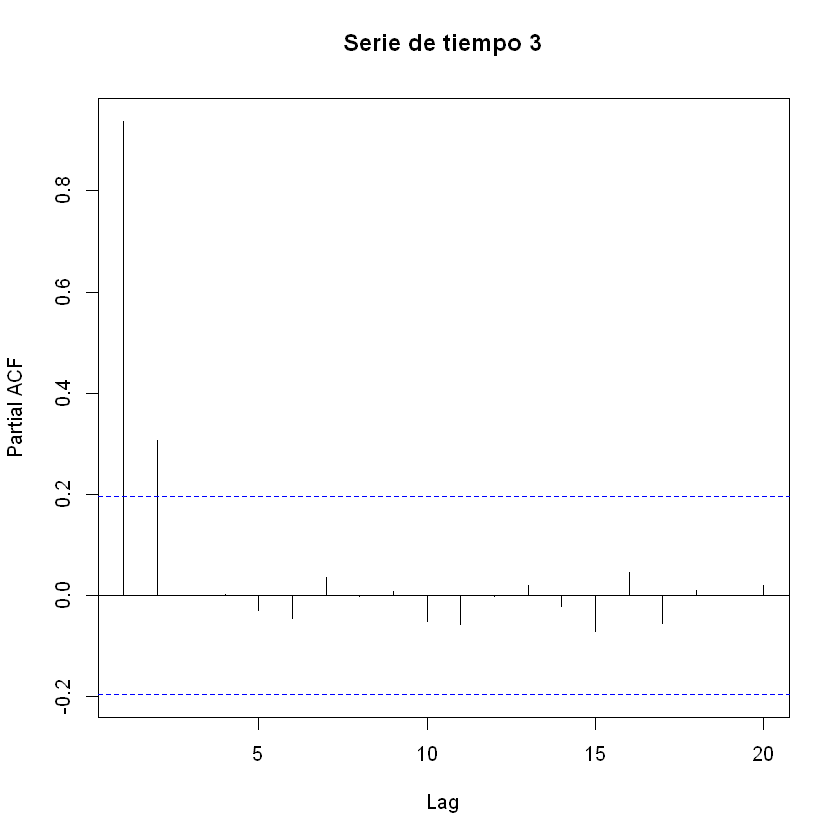
AR(2):

arima(estacional2[,2], order = c(2, 0, 0))

Call:
arima(x = estacional2[, 2], order = c(2, 0, 0))

Coefficients:
         ar1      ar2  intercept
      1.2752  -0.3108     1.6528
s.e.  0.0967   0.0979     0.6029

sigma^2 estimated as 0.06309:  log likelihood = -5.3,  aic = 18.59

\[\hat{z_t} = 1,6528 + 1,2752 z_{t-1}-0,3108 z_{t-2}\]

Ejemplo 4: serie Ruido Blanco

p4

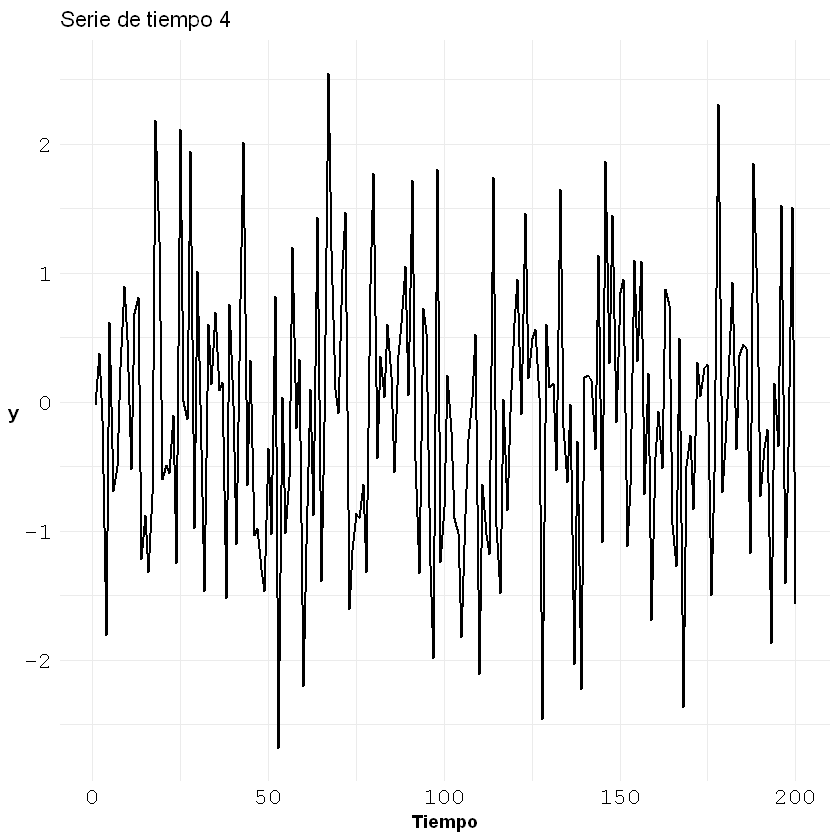
pacf(ruidoblanco[,2], main = "Serie de tiempo 4")

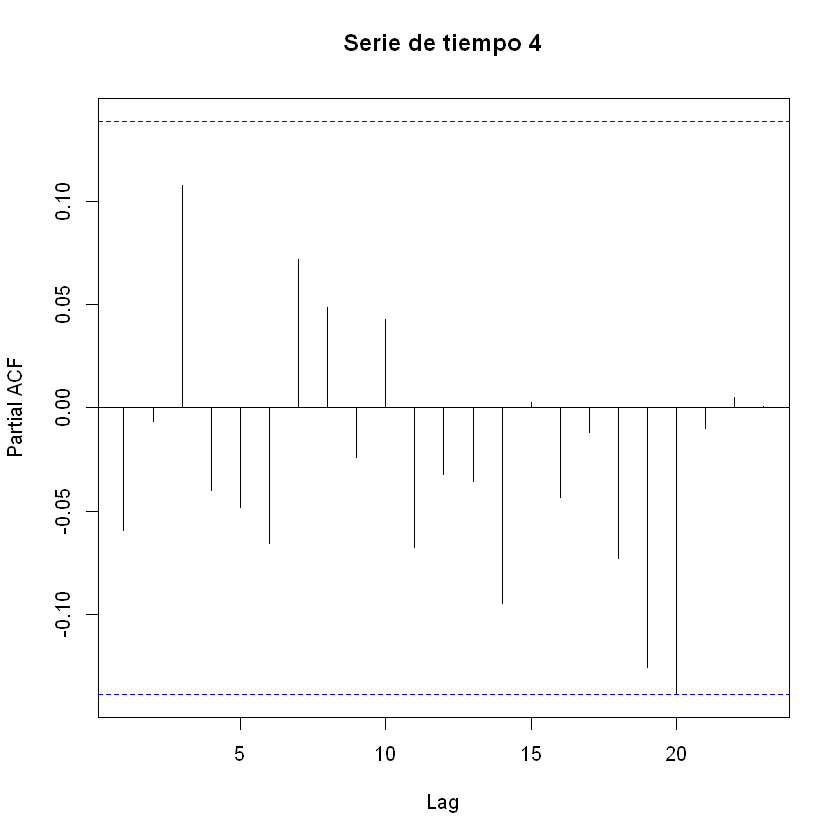
No es una serie con dependencia a los valores históricos. Se puede hacer la estimación de cualquier modelo AR(p), pero el valor de los coeficientes será cercanos a cero, son no significativos. No tiene sentido modelar un ruido blanco. En la siguiente estimación de un AR(1) el coeficiente \(\phi_1\) tien un valor cercano a cero.

arima(ruidoblanco[,2], order = c(1, 0, 0))

Call:
arima(x = ruidoblanco[, 2], order = c(1, 0, 0))

Coefficients:
          ar1  intercept
      -0.0597    -0.1104
s.e.   0.0708     0.0688

sigma^2 estimated as 1.061:  log likelihood = -289.72,  aic = 585.43