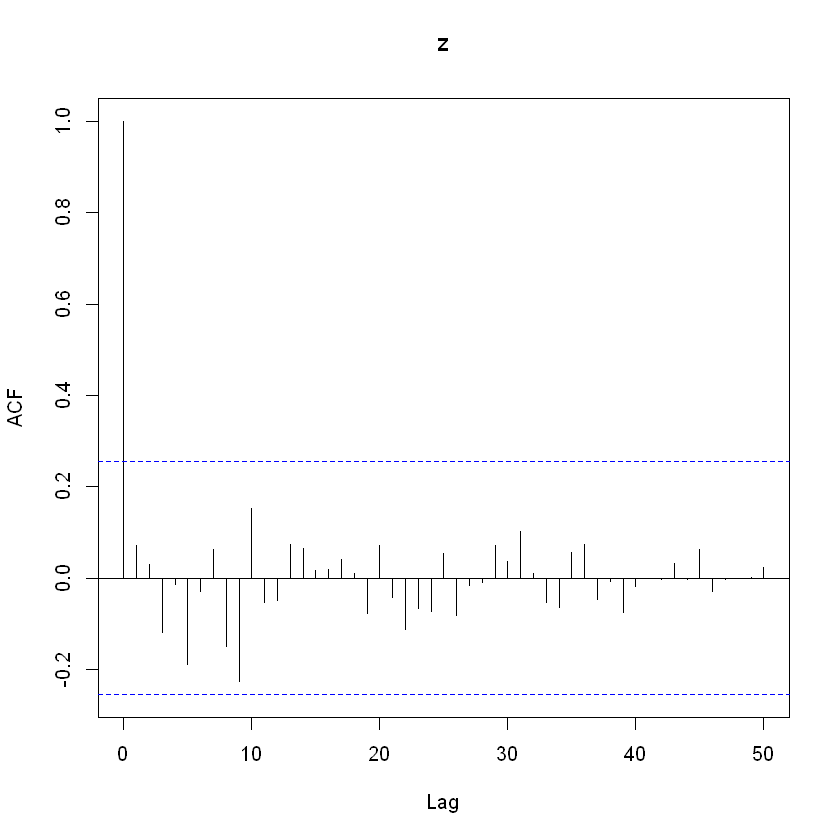ACF
La covarianza mide el movimiento conjunto (co-movimiento) entre dos variables aleatorias. En las series de tiempo univariadas donde tenemos una sola variable aleatoria, la covarianza se aplica para medir la relación entre varios puntos en el tiempo de la misma serie temporal, es decir, se puede calcular la covarianza entre el valor \(z_t\) y el valor \(z_{t-1}\) (un período anterior). También se podría hacer entre \(z_t\) y \(z_{t-2}\), que es la covarianza entre dos períodos. Estos períodos anteriores se llaman rezagos, en inglés lags y se denominan con la letra \(k\).
La covarianza entre los rezagos \(k\) de una serie de tiempo se llama autocovarianza \(\gamma_k\) y se define como:
Las covarianzas tienen las mismas unidades que la variable por lo que es difícil concluir la dimensión del movimiento conjunto, pero una forma estándar de medir el movimiento conjunto es con el coeficiente de correlación que parte de la covarianza, pero se divide por la varianza entre las variables y el resultado siempre estará entre \(-1\) y \(1\).
La correlación entre los rezagos \(k\) de una serie de tiempo se llama autocorrelación \(\rho_k\) y se define como:
Como solo se tiene una variable aleatoria que es la serie de tiempo, entonces el denominador es solo la varianza de la serie \(\sigma_z^2\) así:
Para:
Donde:
Una forma para estimar la covarianza \(\gamma_k\) para una serie estacionaria de \(N\) observaciones es:
Así que la autocorrelación se puede reescribir como:
La autocorrelación siempre estará entre \(-1\) y \(1\). Valores cercanos a \(1\) significan que las observaciones separadas \(k\) unidades de tiempo tienen una fuerte tendencia a moverse juntas en forma lineal con pendiente positiva, es decir, tienen alta correlación. En cambio, con ACF cercana a \(-1\) las observaciones con un lag de \(k\) unidades de tiempo tienen una fuerte tendencia a moverse juntas en forma lineal con pendiente negativa, es decir, tienen correlación inversa.
Función de Autocorrelación (ACF):
El gráfico del coeficiente de autocorrelación, \(\rho_k\), en función de los rezagos \(k\), es llamado Función de Autocorrelación (ACF) (sample autocorrelation function). Anteriomente se le llamaba correlograma.
Debido a que la matriz de coeficientes de correlación es simétrica, se cumple que \(\rho_k=\rho_{-k}\), por tanto, solo es necesario graficar la parte positiva \(k\).
En la práctica, para obtener una estimación útil de la función de autocorrelación, se necesita al menos 50 observaciones y la estimación de autocorrelación \(\rho_k\), debería ser calculada hasta un máximo de \(k=\frac{N}{4}\).
Para un proceso estacionario, la varianza \(\sigma_z^2\) es igual a la autocovarianza \(\gamma_0\) \((\sigma_z^2=\gamma_0)\) y es la misma en el tiempo \(𝑡 - 𝑘\) como en el tiempo \(𝑡\). Por lo tanto, la autocorrelación en el rezago \(𝑘\), es decir, la correlación entre \(z_t\) y \(z_{t-k}\) es:
Lo anterior implica que \(\rho_0=1\). Es común encontrar el ACF donde se grafica a partir del cero donde \(k=0\) y siempre tendrá una autocorrelación igual a la unidad (la correlación de una variable con ella misma siempre es 1).
ACF series estacionales:
Ejemplo 1:
Utilizar el archivo Estacionalidad.csv que contiene 100
observaciones.
estacional <- read.csv("Estacionalidad.csv", sep = ",", dec = ".", header = T)
library(ggplot2)
ggplot()+geom_line(aes(x = c(1:nrow(estacional)), y = estacional[,1]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
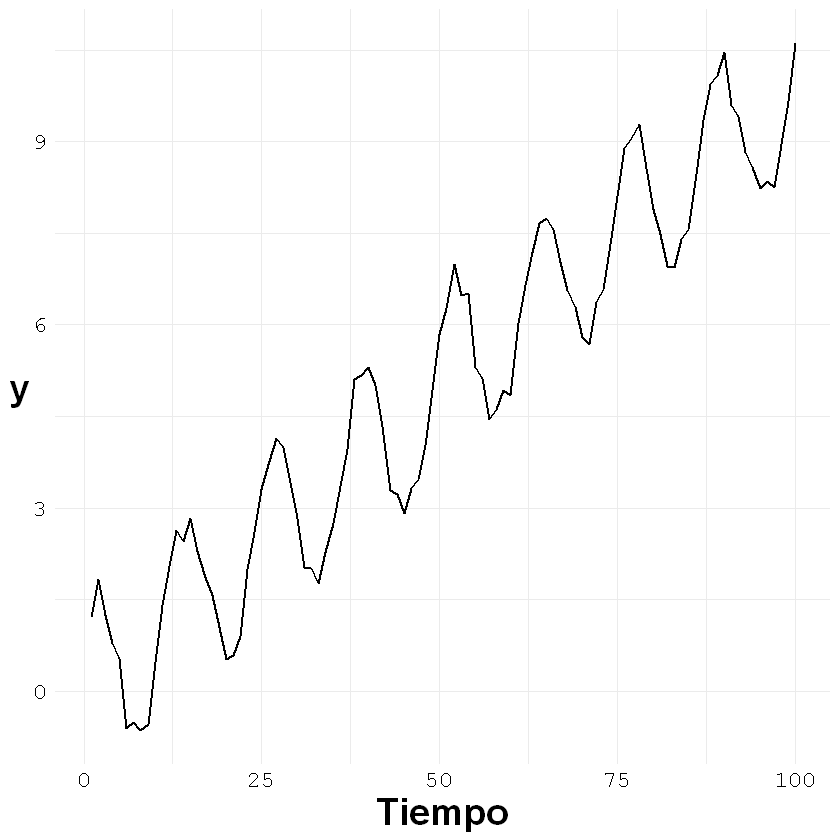
La serie de tiempo para hacer los cálculos la llamaremos \(z\).
z <- estacional[,1]
print(head(z))
[1] 1.2026828 1.8367861 1.2442082 0.7727209 0.5337453 -0.6102938
La serie de tiempo \(z\) tiene \(N = 100\) observaciones.
N <- length(z)
print(N)
[1] 100
Los rezagos se denominarán \(k\).
Para el primer rezago \(k=1\).
k <- 1
\(z_t\) será la serie de tiempo sin los últimos \(k\) valores.
z_t <- z[1:(length(z)-k)]
print(head(z_t))
[1] 1.2026828 1.8367861 1.2442082 0.7727209 0.5337453 -0.6102938
\(z_t\) será la serie de tiempo que empieza desde el rezago \(k\).
z_k <- z[(k + 1):length(z)]
print(head(z_k))
[1] 1.8367861 1.2442082 0.7727209 0.5337453 -0.6102938 -0.5144100
La varianza de la serie de tiempo \(z\) es:
var_z <- (sum((z - mean(z))^2))/N
print(var_z)
[1] 8.974702
La autocorrelación para rezago \(k=1\) es:
rho_k <- sum((z_t - mean(z))*(z_k - mean(z)))/(N*var_z)
print(rho_k)
[1] 0.9564429
El valor del AFC para el primer rezago es 0,956, este valor está muy cercano a la unidad, por tanto, la serie de tiempo tiene alta dependencia de la observación del período anterior.
Para \(k=2\):
k <- 2
z_t <- z[1:(length(z)-k)]
z_k <- z[(k + 1):length(z)]
rho_k <- sum((z_t - mean(z))*(z_k - mean(z)))/(N*var_z)
print(rho_k)
[1] 0.9026627
La serie de tiempo también tiene alta dependencia con el segundo rezago porque el AFC para \(k=2\) es 0,903.
Podemos utilizar un ciclo for para calcular varios valores de ACF.
rho_k <- vector()
for(k in 1:25){
z_t <- z[1:(length(z)-k)]
z_k <- z[(k + 1):length(z)]
rho_k[k] <- sum((z_t - mean(z))*(z_k - mean(z)))/(N*var_z)
}
ggplot()+geom_bar(aes(x = c(1:25), y = rho_k), stat = "identity", position = "identity")+
theme_minimal()
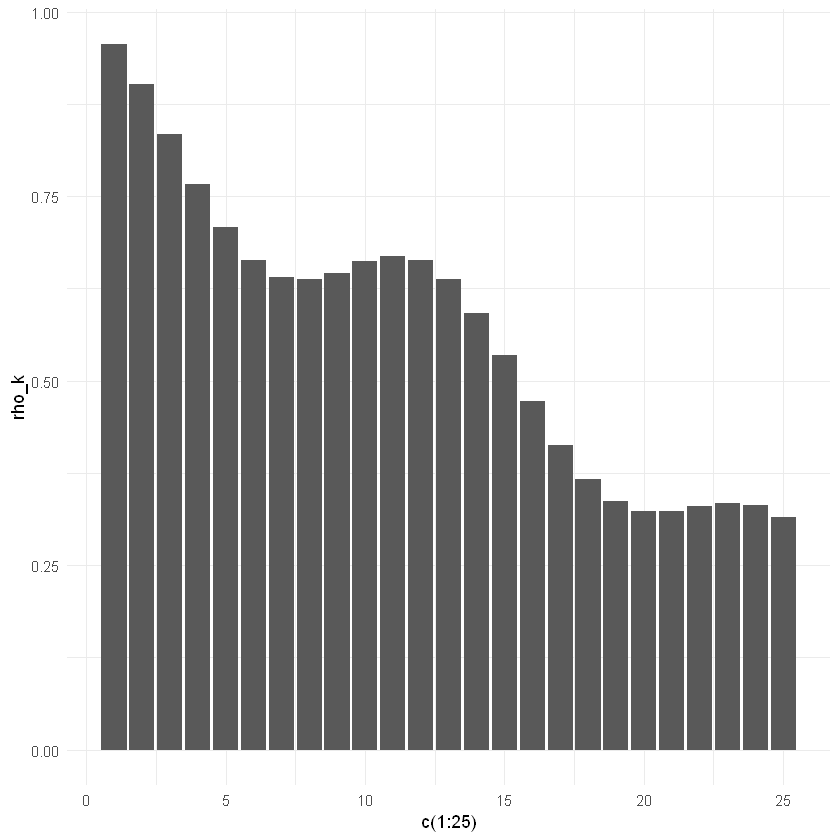
La relación lineal entre los rezagos los podemos ver en un gráfico de nubes de puntos así:
ggplot()+geom_point(aes(x = z_t, y = z_k))+
theme_minimal()
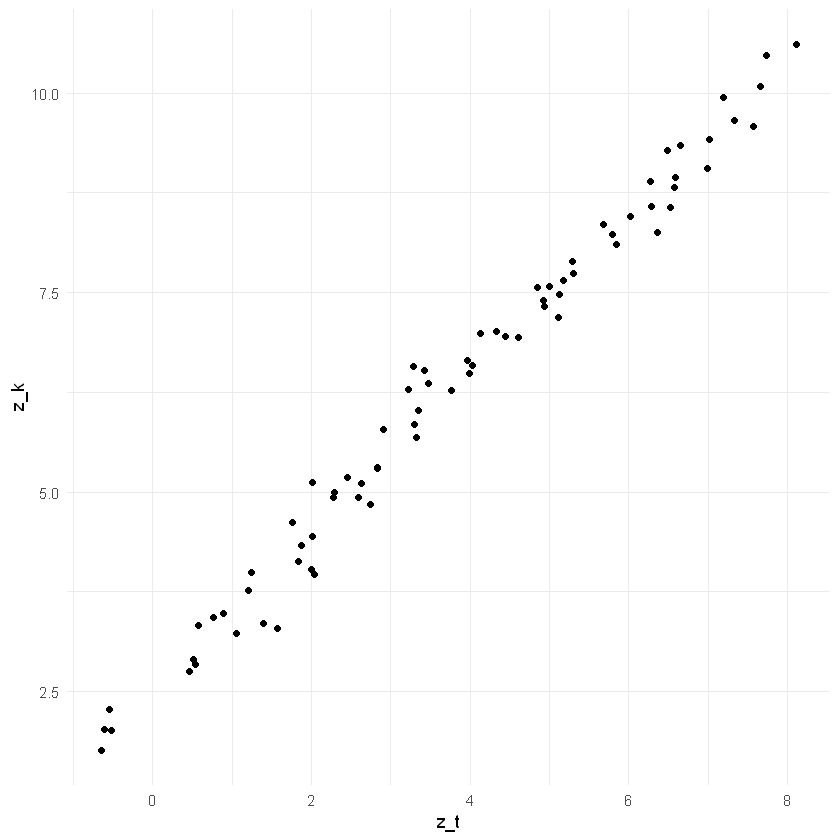
El gráfico anterior muestra que la serie de tiempo tiene alta dependencia con el primer rezago. Esto también se puede aplicar para los demás rezagos, pero lo común es graficar solamente la función de autocorrelación.
Función acf de R:
Podemos utilizar la función acf() de la librería stats para
calcular los valores del ACF y mostrar la gráfica.
acf <- acf(z, lag.max = 25)
acf
Autocorrelations of series 'z', by lag
0 1 2 3 4 5 6 7 8 9 10 11 12
1.000 0.956 0.903 0.835 0.767 0.708 0.664 0.640 0.638 0.646 0.662 0.669 0.664
13 14 15 16 17 18 19 20 21 22 23 24 25
0.637 0.592 0.535 0.473 0.413 0.367 0.337 0.323 0.323 0.330 0.335 0.332 0.316
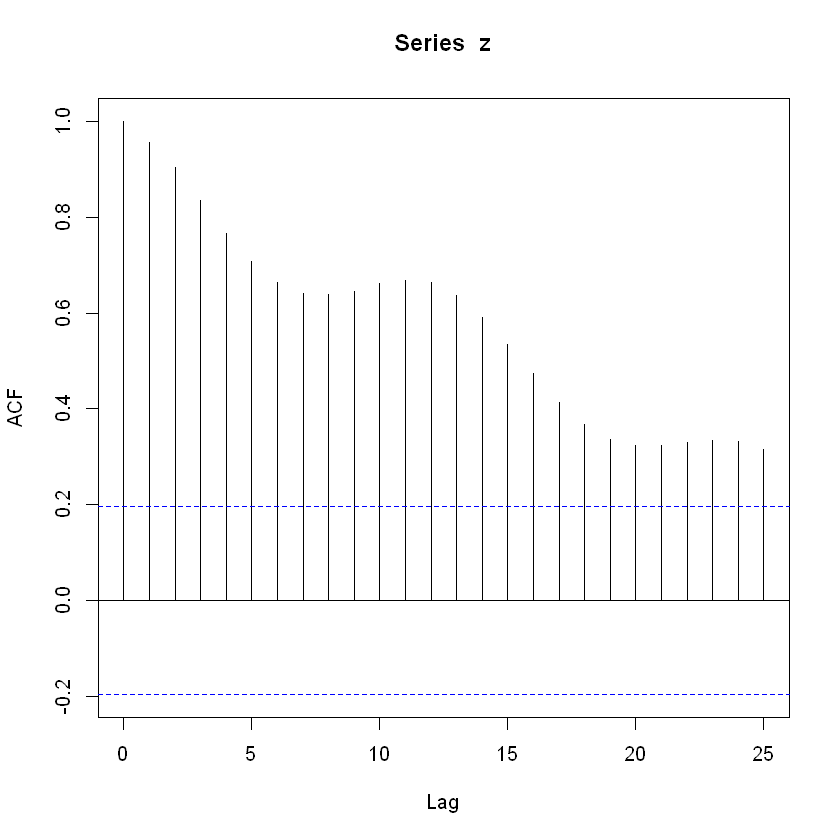
El comportamiento anterior de la ACF es común en las series de tiempo estacionales.
Ejemplo 2:
Utilizar el archivo Estacionalidad2.csv que contiene 100
observaciones.
estacional2 <- read.csv("Estacionalidad2.csv", sep = ",", dec = ".", header = T)
ggplot()+geom_line(aes(x = c(1:nrow(estacional2)), y = estacional2[,2]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
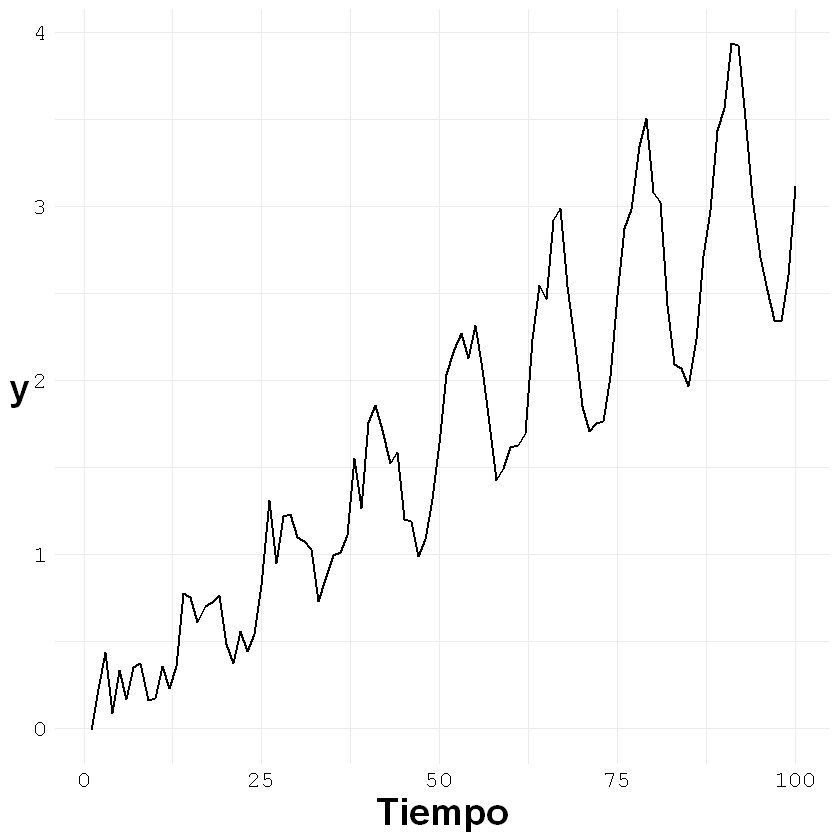
acf(estacional2[,2], lag.max = 25)
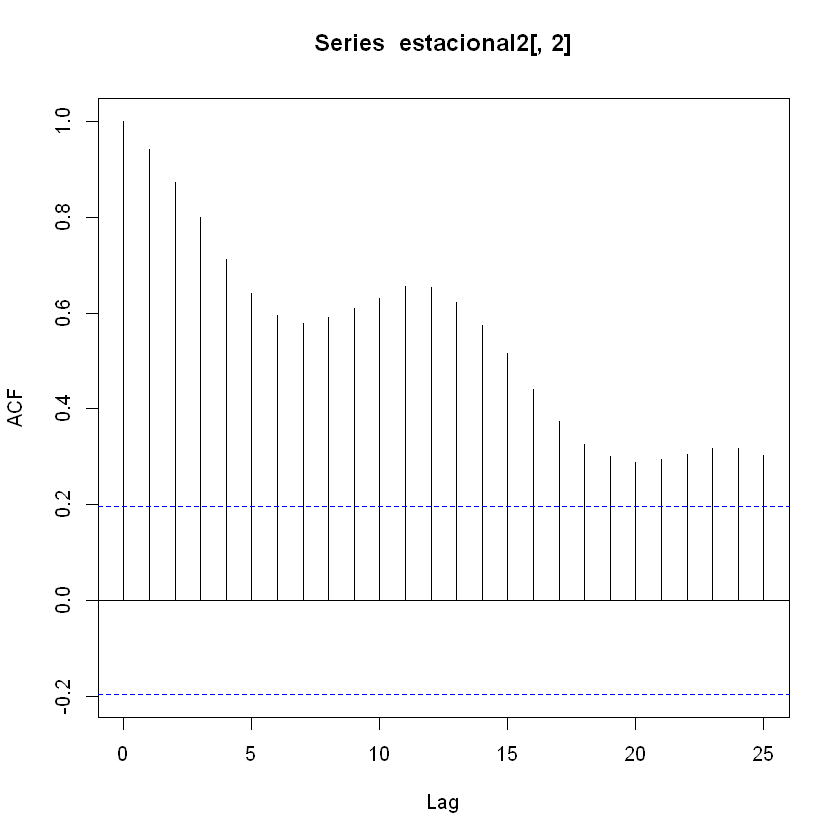
ACF series con tendencia:
Utilizar el archivo Tendencia.csv que contiene 100 observaciones.
tendencia <- read.csv("Tendencia.csv", sep = ",", dec = ".", header = T)
ggplot()+geom_line(aes(x = c(1:nrow(tendencia)), y = tendencia[,2]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
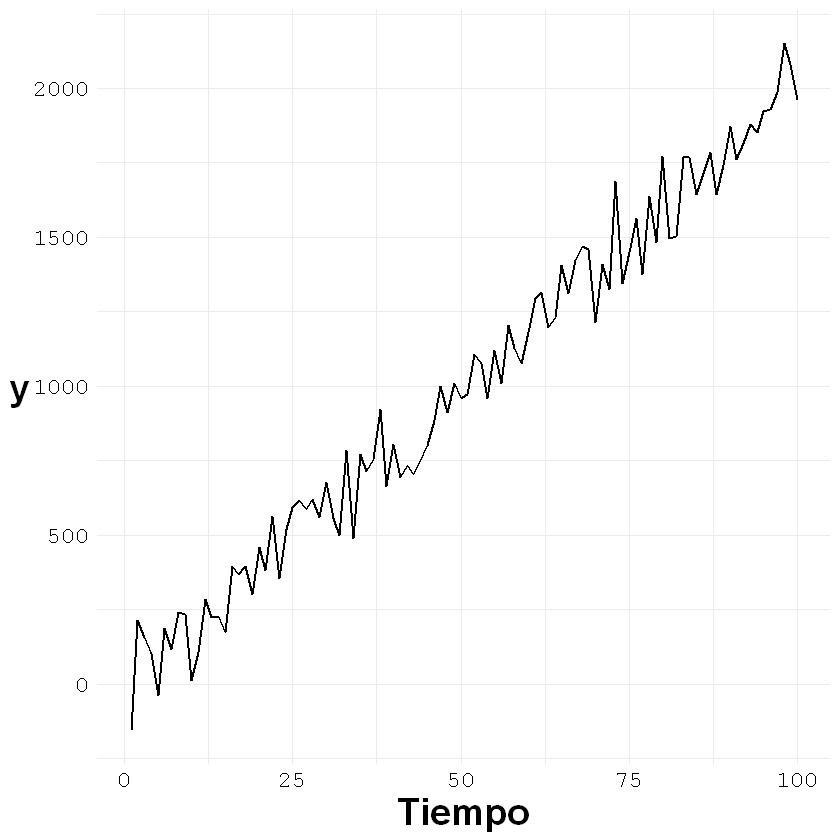
acf(tendencia[,2], lag.max = 25)
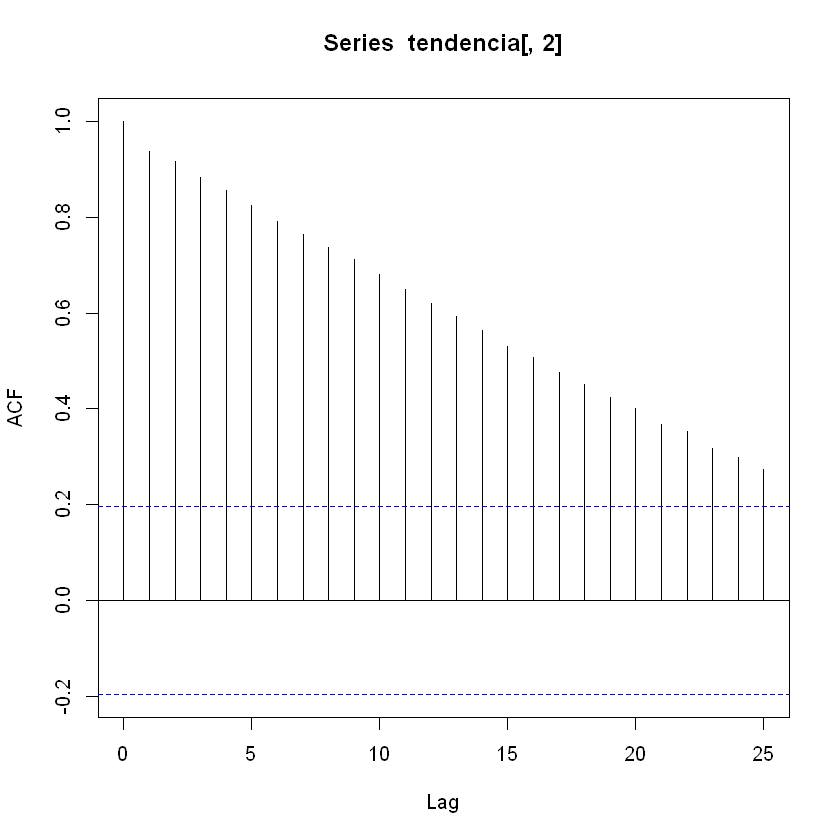
ACF series sin tendencia:
Utilizar el archivo Ejemplo3.csv que contiene 100 observaciones.
ejemplo3 <- read.csv("Ejemplo3.csv", sep = ",", dec = ".", header = T)
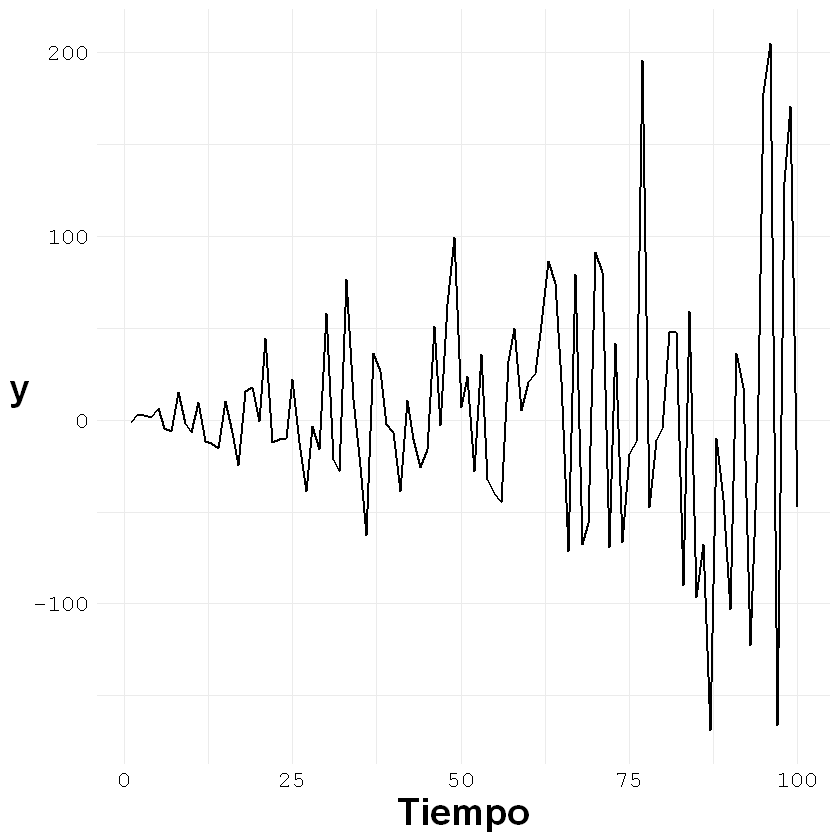
ggplot()+geom_line(aes(x = c(1:nrow(ejemplo3)), y = ejemplo3[,2]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
acf(ejemplo3[,2], lag.max = 25)
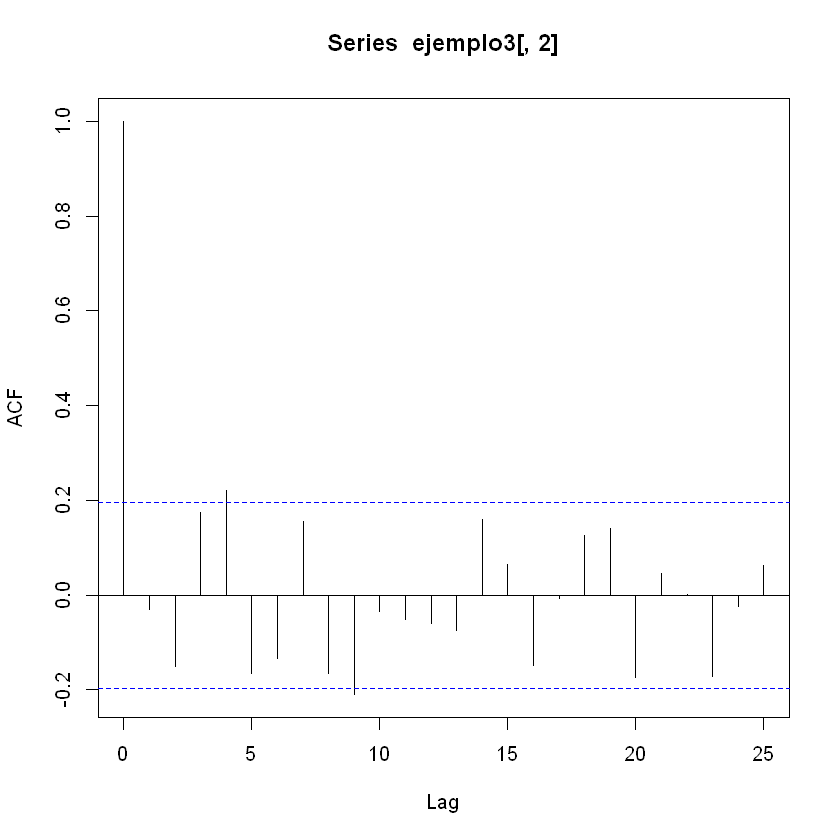
ACF series Ruido Blanco:
Utilizar el archivo RuidoBlanco.csv que contiene 200 observaciones.
ruidoblanco <- read.csv("RuidoBlanco.csv", sep = ",", dec = ".", header = T)
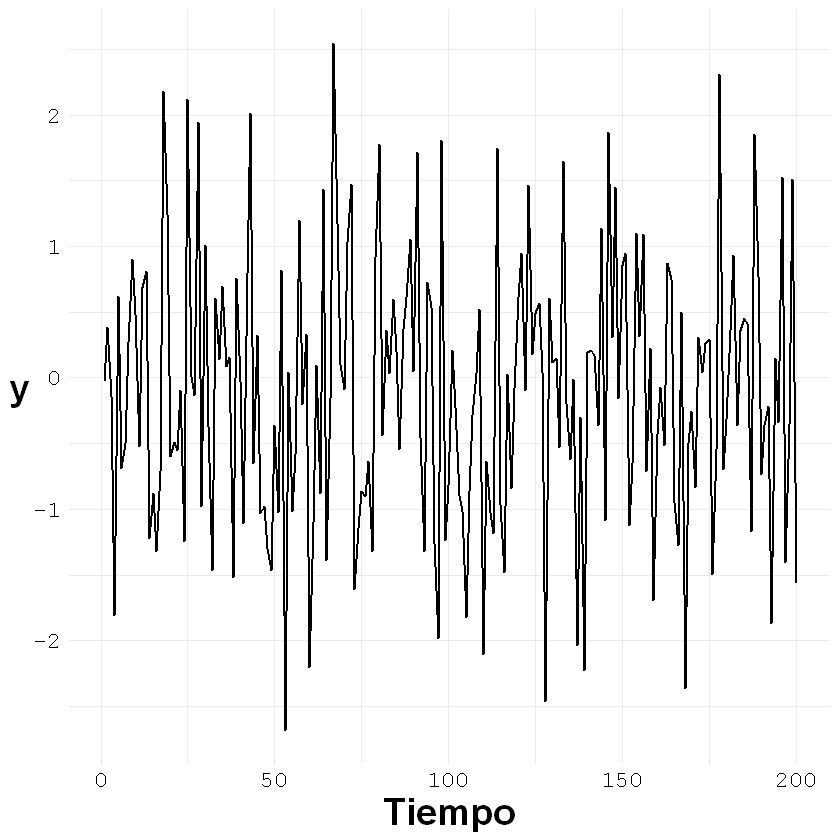
ggplot()+geom_line(aes(x = c(1:nrow(ruidoblanco)), y = ruidoblanco[,2]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
acf(ruidoblanco[,2], lag.max = 50)
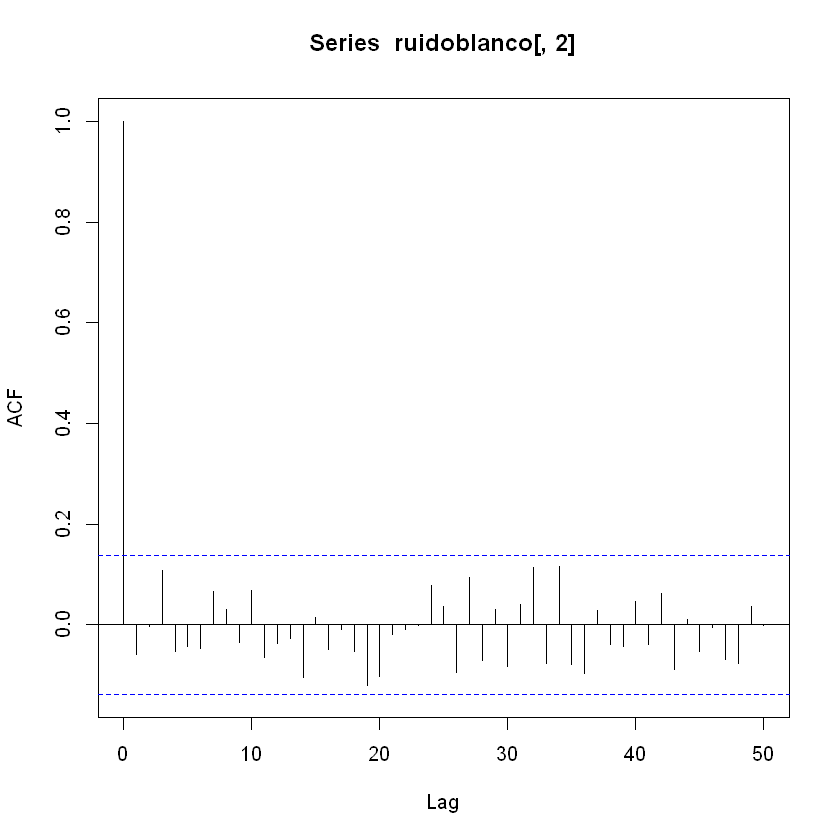
En los procesos de ruido blanco cada observación es independiente de las demás y no hay autocorrelación.
Prueba con la ACF:
Con la Función de Autocorrelación (ACF) se prueban las siguientes hipótesis:
\(H_0:\) \(\rho_k = 0\)
\(H_1:\) \(\rho_k \neq 0\)
La hipótesis nula indica que la serie de tiempo es estacionaria gaussiana, es decir, \(H_0\) indica que la serie de tiempo es ruido blanco.
El error estándar (se) (standard error) de \(\rho_k\) es:
Para \(k>0\)
El límite de \(2\pm se[\rho_k]\) se usa para determinar bajo el supuesto de que la serie es completamente aleatoria, es decir, ruido blanco. Los valores de \(\rho_k\) mayores a \(2\pm se[\rho_k]\) se concluyen que son mayores que cero.
Con la hipótesis nula de que el proceso es ruido blanco, \(\rho_k\) converge a una distribución normal cero y varianza igual a \(\frac{1}{N}\). Esta varianza es útil para probar la significancia de las autocorrelaciones estimadas. Los gráficos de la ACF tienen una franja de líneas punteadas que representan la significancia de cada \(\rho_k\), esta franja son \(\pm 2\) desviaciones estándar de \(\rho_k\) \((\pm 2 \times se[\rho_k]=\pm \frac{2}{\sqrt{(N)}})\).
Por tanto, si \(\rho_k\) está por fuera del rango \(\frac{2}{\sqrt{(N)}}\), la serie de tiempo no es ruido blanco porque tiene alta dependencia al rezago \(k\).
Comportamiento de la ACF:
Para series de tiempo no estacional, la ACF puede mostrar varios comportamientos.
Si ACF \(\rho_k\) es grande se rechaza la hipótesis nula de que la autocorrelación teórica en el rezago \(k\) es igual a cero.
Los comportamientos más comunes de la AFC son:
Los valores de la ACF disminuyen notoriamente después del lag 2 \((k=2)\).
Los valores de la ACF disminuyen lentamente a medida que aumenta \(k\) (caída exponencial).
Un gráfico en forma de seno.
Disminución en forma exponencial con oscilación.
La siguiente figura muestra una caída rápida de la ACF después del desfase 2.
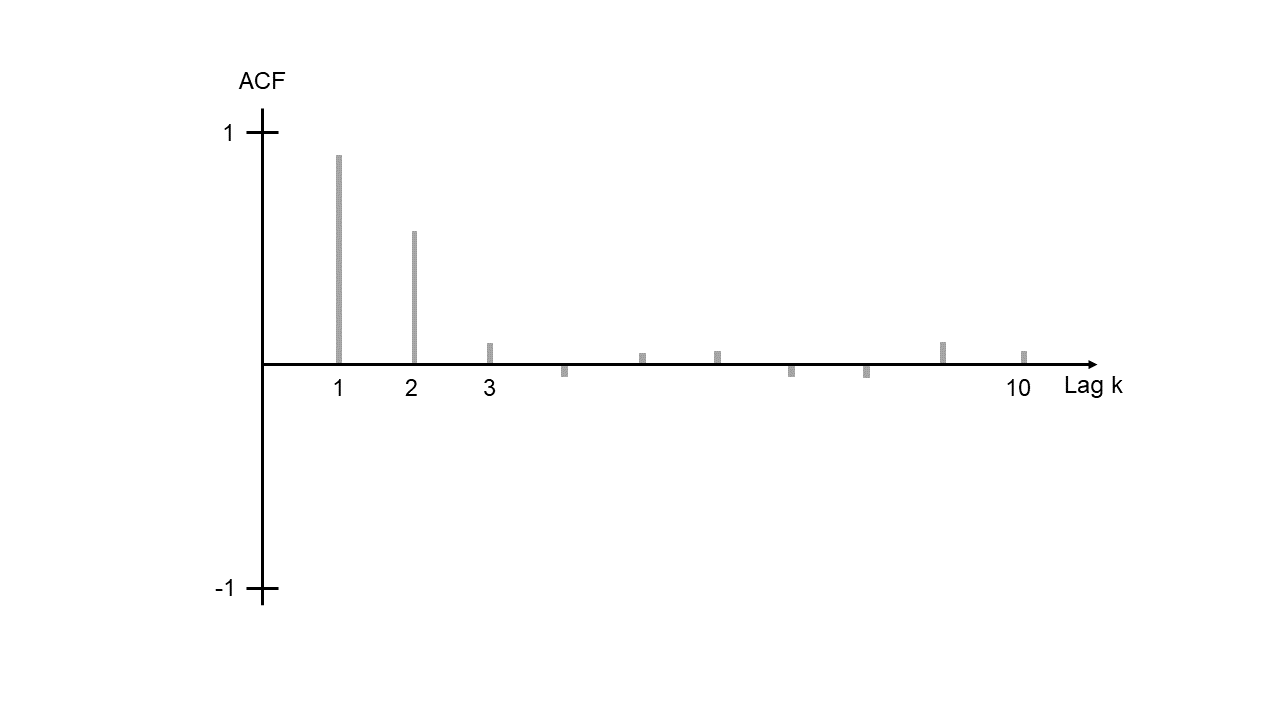
ACF1
La siguiente figura muestra una caída exponencial de la ACF.
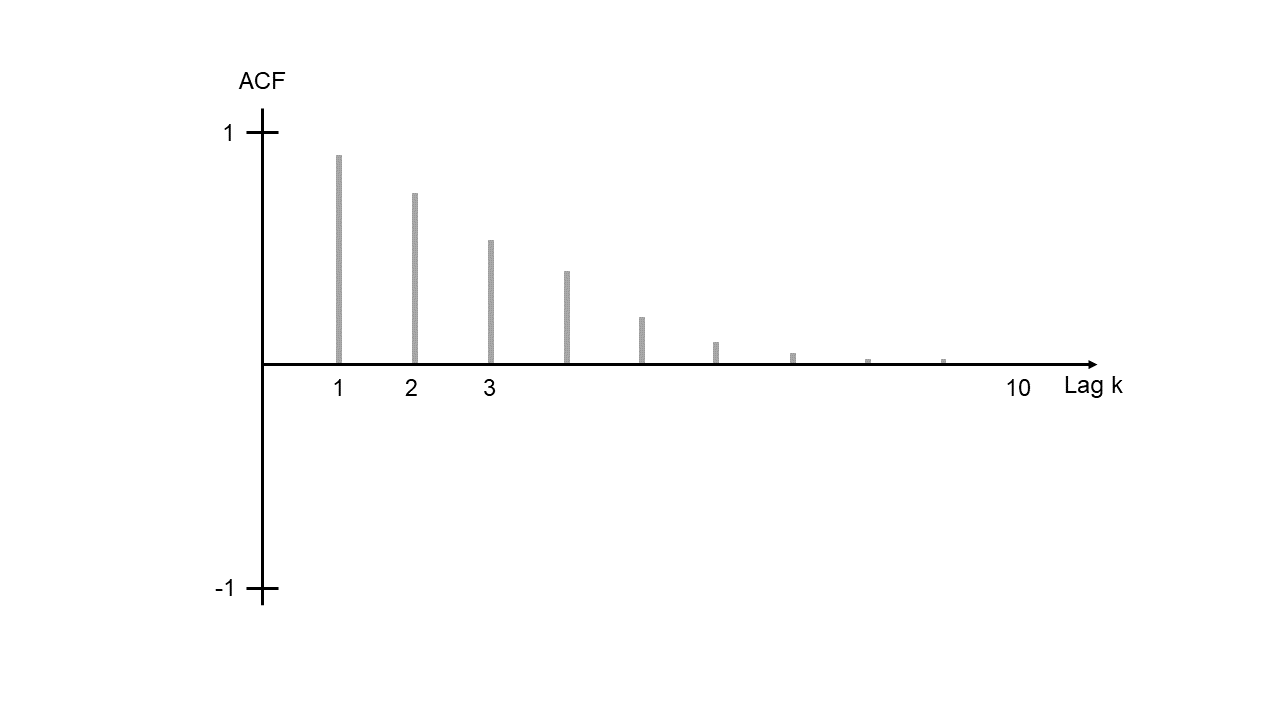
ACF2
La siguiente figura muestra una caída de la ACF en forma de seno.
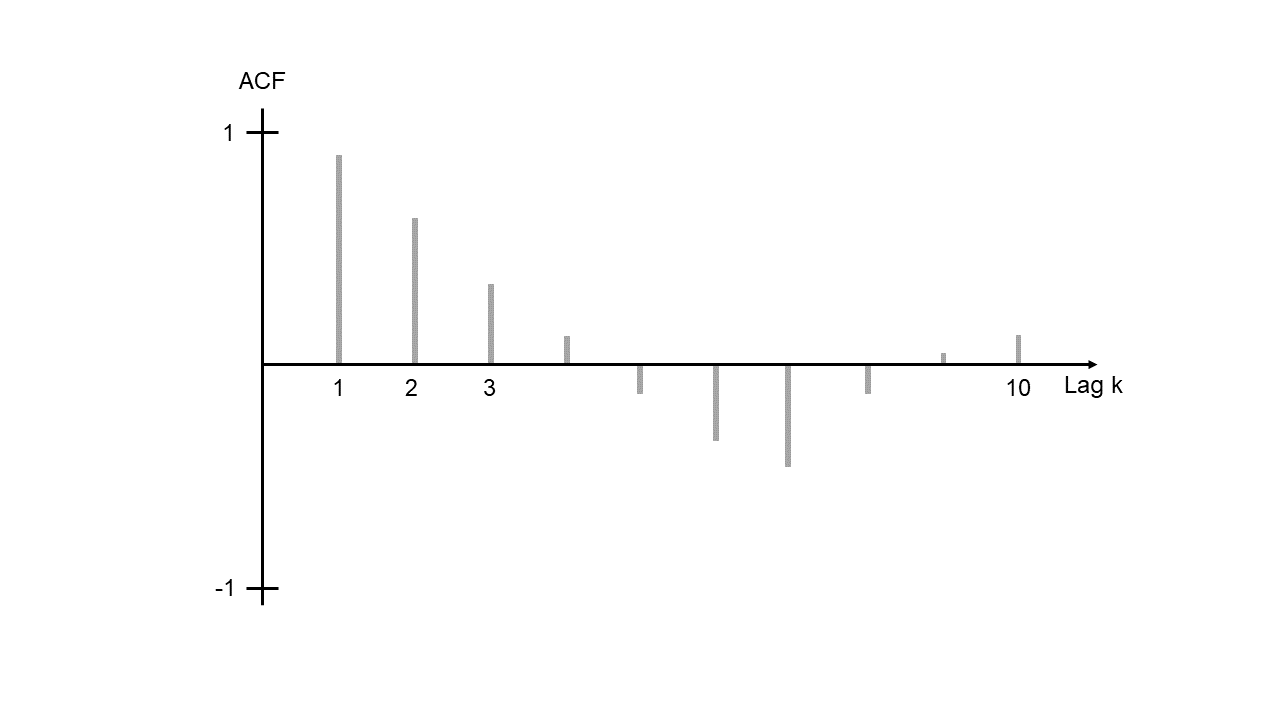
ACF3
La siguiente figura muestra una caída exponencial de la ACF, pero con oscilación.
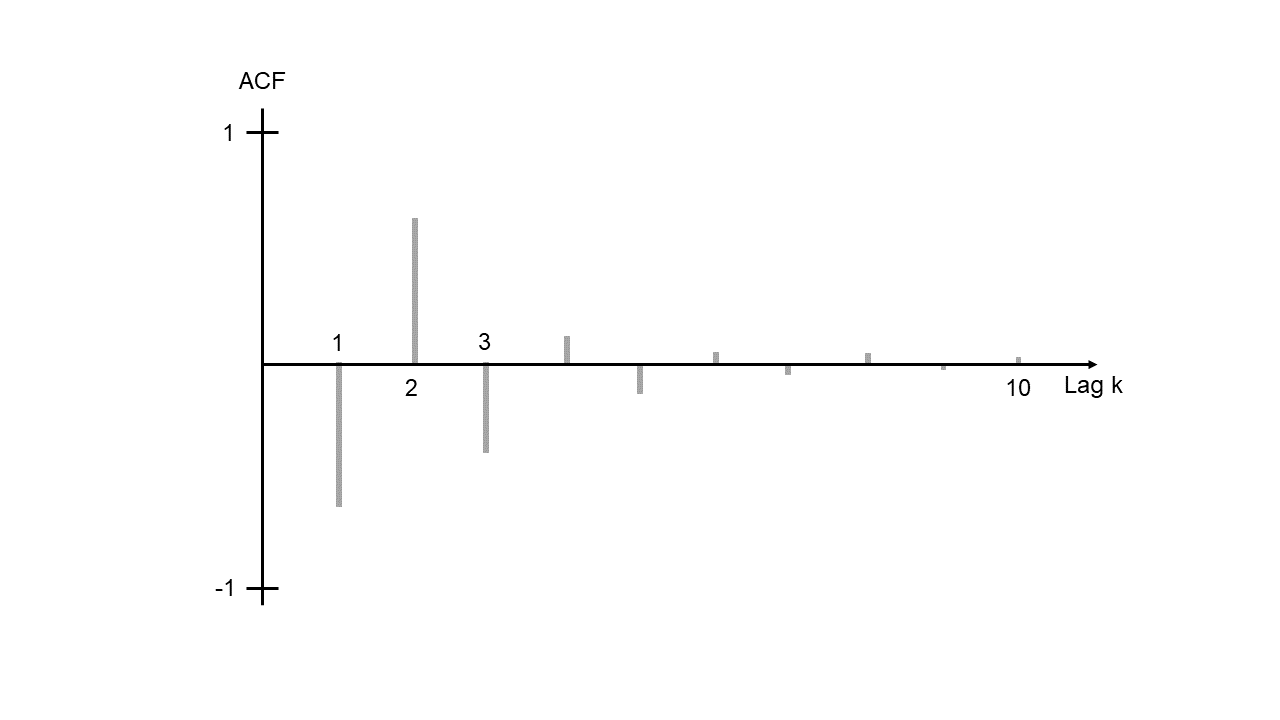
ACF4
Conclusión con la ACF:
Podemos concluir lo siguiente para series de tiempo no estacional:
Si los valores de la ACF caen rápidamente se debe considerar la serie de tiempo como estacionaria, por lo general caen en \(k=2\).
Si los valores de la ACF caen lentamente se debe considerar la serie de tiempo como no estacionaria.
Primero se debe calcular la ACF a la serie de tiempo original, si los valores de la ACF caen rápidamente, la serie de tiempo es estacionaria, pero si se muestra un caimiento lento, la serie de tiempo es no estacionaria y se debe transformar la serie de tiempo con las primeras diferencias (primer orden). Luego, se calcula la ACF para la serie transformada y se verifica si los datos de las primeras diferencias son estacionarios o no, en caso de una caída lenta de la ACF, se considera los datos como no estacionarios y se transforman los datos para obtener las segundas diferencias (segundo orden) con el fin de obtener datos estacionarios con un comportamiento de la ACF con caída rápida.
Transformación de las series de tiempo:
Las series de tiempo se transforman con el objetivo de obtener una nueva serie de tiempo estacionaria.
Una serie de tiempo transformada con las primeras diferencias (primer orden) es:
Una serie de tiempo transformada con las segundas diferencias (segundo orden) son las primeras diferencias de las primeras diferencias:
En R se pueden calcular estas diferencias así:
z = diff(z, lag = 1, differences = 1)
Para el segundo orden se utiliza:
z = diff(z, lag = 1, differences = 2)
Ejemplos: diferencias de primer orden
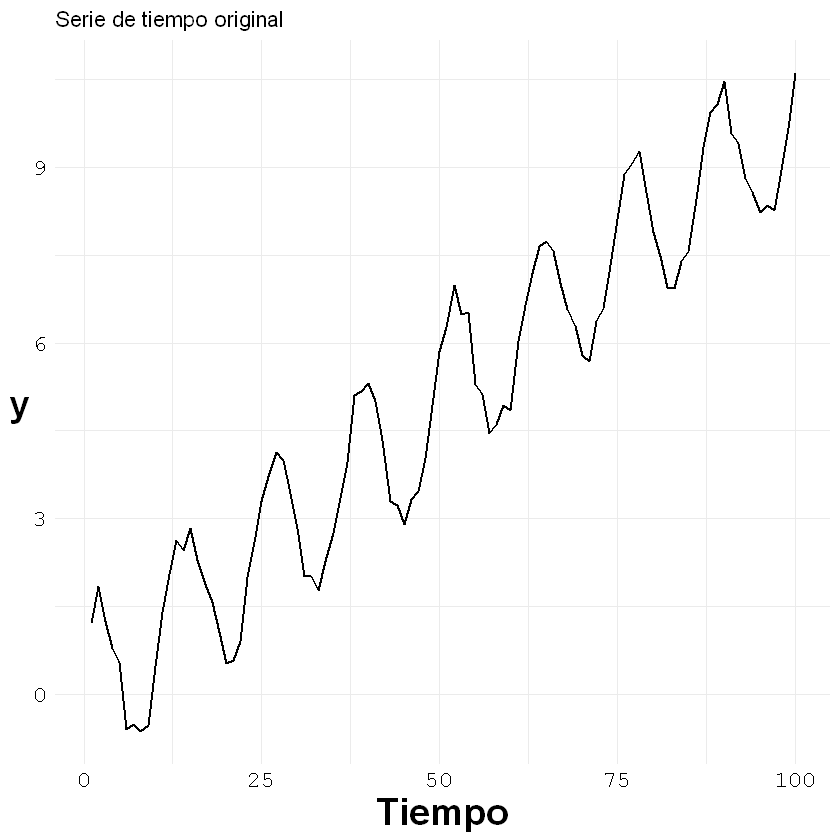
Serie estacional:
z <- diff(estacional[,1], lag = 1, differences = 1)
ggplot()+geom_line(aes(x = c(1:length(estacional[,1])), y = estacional[,1]), size = 0.7)+
theme_minimal() +
labs(title = "Serie de tiempo original", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
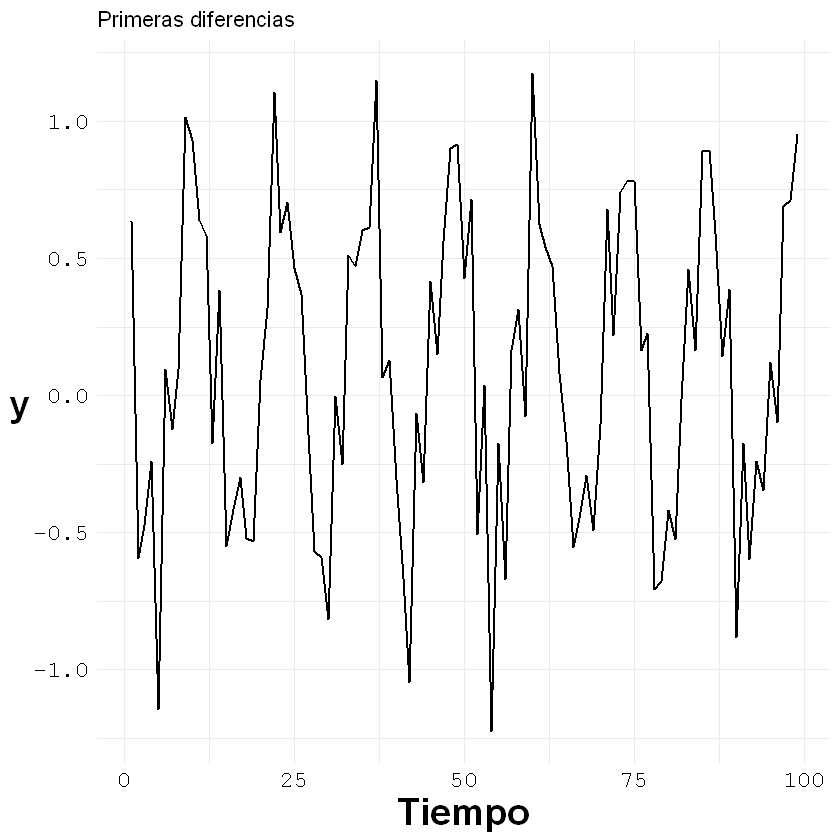
ggplot()+geom_line(aes(x = c(1:length(z)), y = z), size = 0.7)+
theme_minimal() +
labs(title = "Primeras diferencias", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
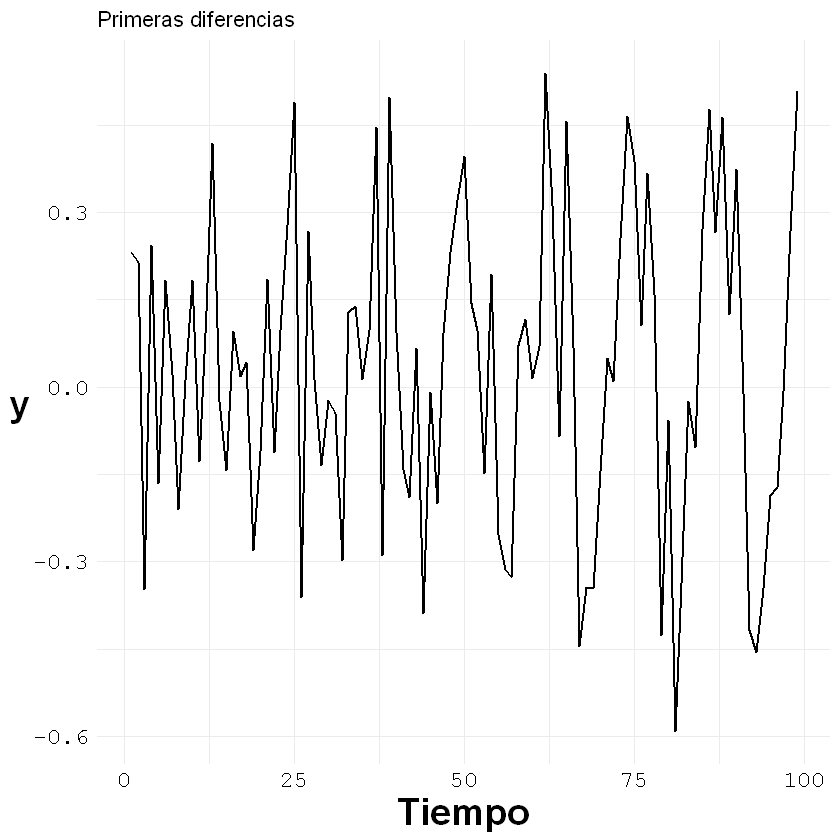
Serie con tendencia:
z <- diff(estacional2[,2], lag = 1, differences = 1)
ggplot()+geom_line(aes(x = c(1:length(estacional2[,2])), y = estacional2[,2]), size = 0.7)+
theme_minimal() +
labs(title = "Serie de tiempo original", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))

ggplot()+geom_line(aes(x = c(1:length(z)), y = z), size = 0.7)+
theme_minimal() +
labs(title = "Primeras diferencias", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
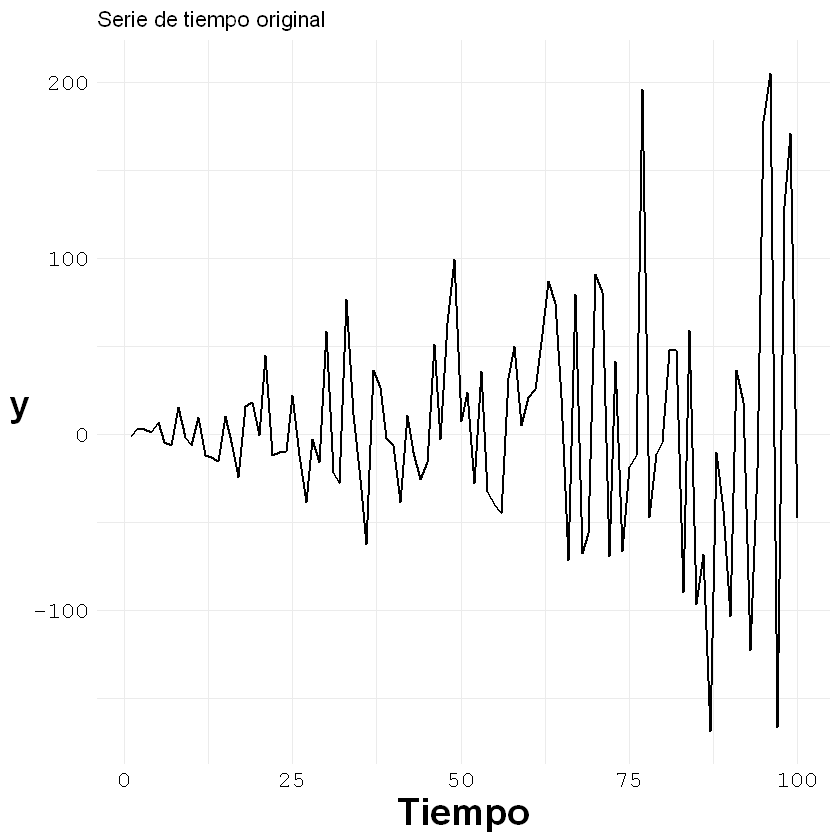
Serie con sin tendencia y varianza no constante:
z <- diff(ejemplo3[,2], lag = 1, differences = 1)
ggplot()+geom_line(aes(x = c(1:length(ejemplo3[,2])), y = ejemplo3[,2]), size = 0.7)+
theme_minimal() +
labs(title = "Serie de tiempo original", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
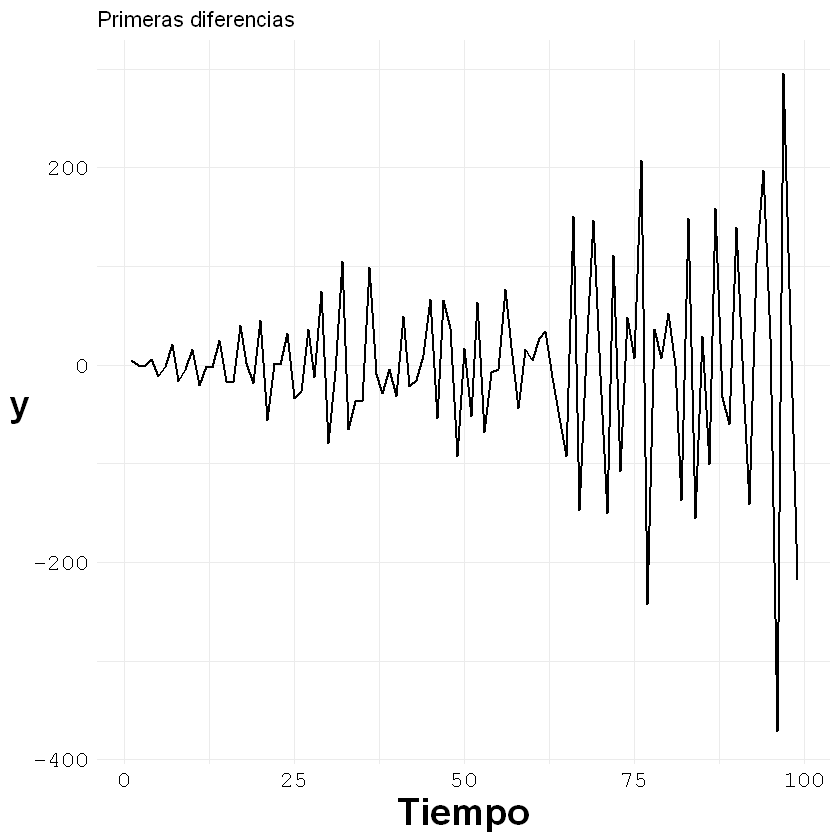
ggplot()+geom_line(aes(x = c(1:length(z)), y = z), size = 0.7)+
theme_minimal() +
labs(title = "Primeras diferencias", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
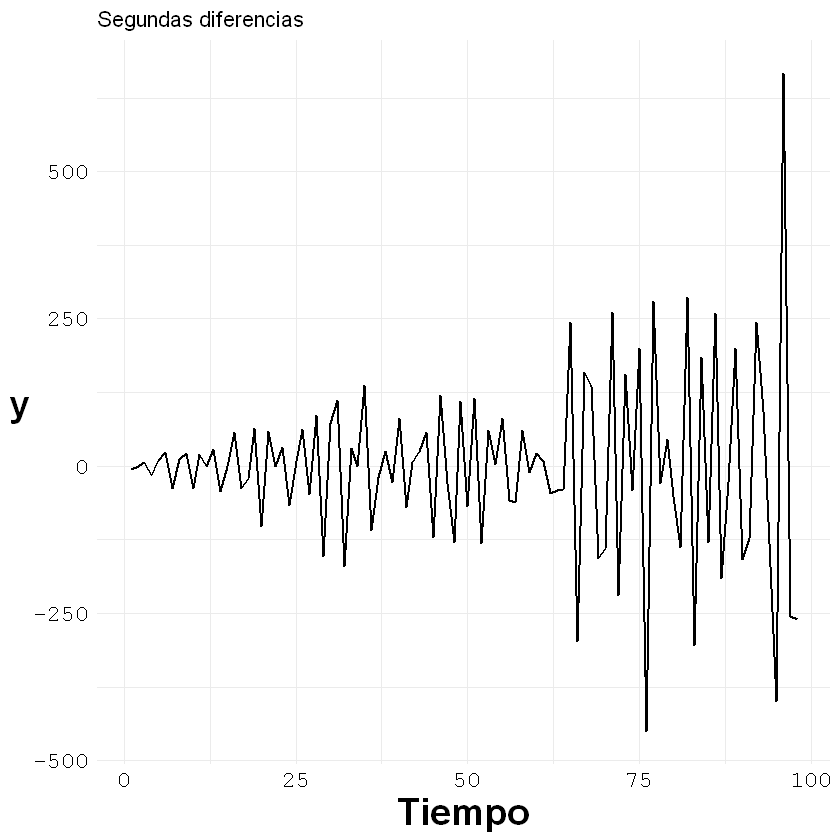
Ejemplo: diferencias de segundo orden
z <- diff(ejemplo3[,2], lag = 1, differences = 2)
ggplot()+geom_line(aes(x = c(1:length(z)), y = z), size = 0.7)+
theme_minimal() +
labs(title = "Segundas diferencias", x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
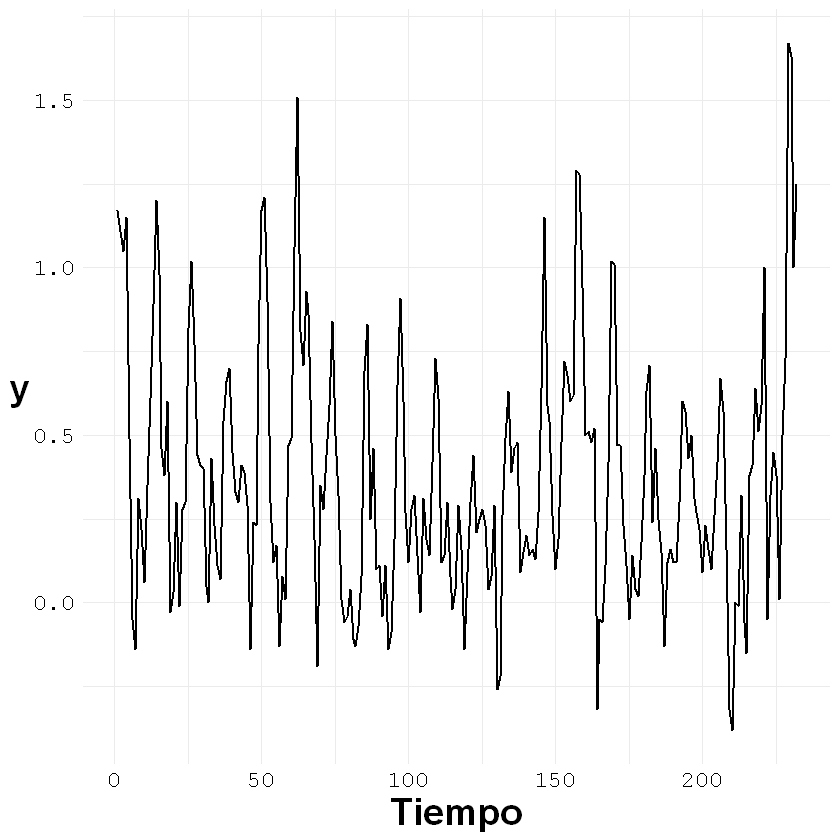
Ejemplo con la variación mensual del IPC:
Utilizar el archivo IPCabril2022.csv
y <- read.csv("IPCabril2022.csv", sep = ";", dec = ",", header = T)
print(head(y))
print(tail(y))
Mes IPC
1 ene-03 1.17
2 feb-03 1.11
3 mar-03 1.05
4 abr-03 1.15
5 may-03 0.49
6 jun-03 -0.05
Mes IPC
227 nov-21 0.50
228 dic-21 0.73
229 ene-22 1.67
230 feb-22 1.63
231 mar-22 1.00
232 abr-22 1.25
ggplot()+geom_line(aes(x = c(1:nrow(y)), y = y[,2]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
acf(y[,2], type = "correlation", lag.max = 50)
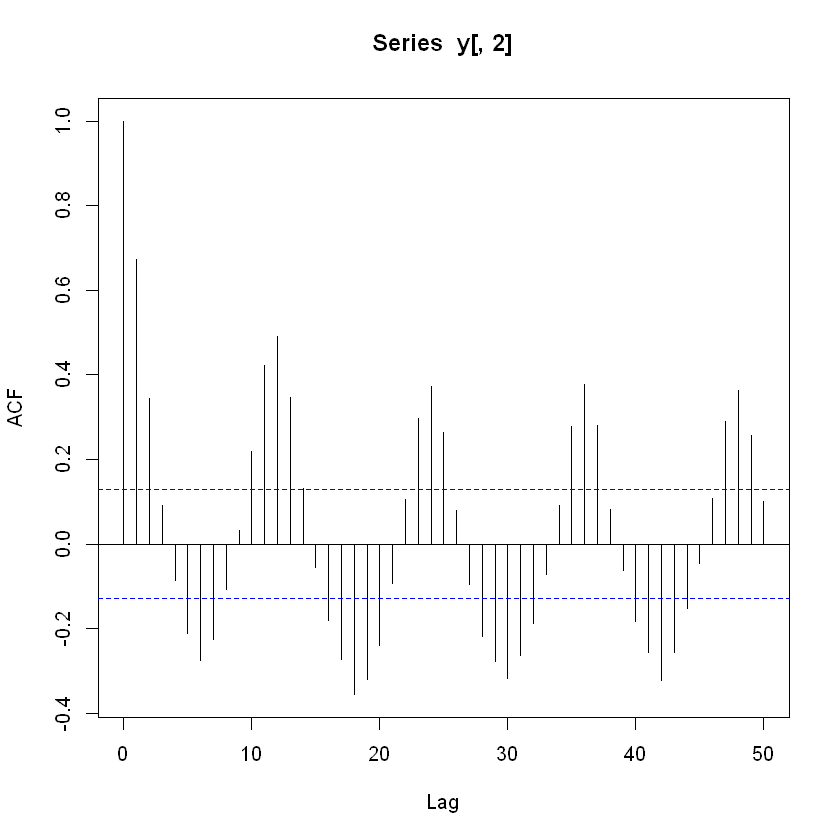
Diferencias de primer orden:
z <- diff(y[,2], lag = 1, differences = 1)
z <- data.frame(z)
print(head(z))
z
1 -0.06
2 -0.06
3 0.10
4 -0.66
5 -0.54
6 -0.09
ggplot()+geom_line(aes(x = c(1:nrow(z)), y = z[,1]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
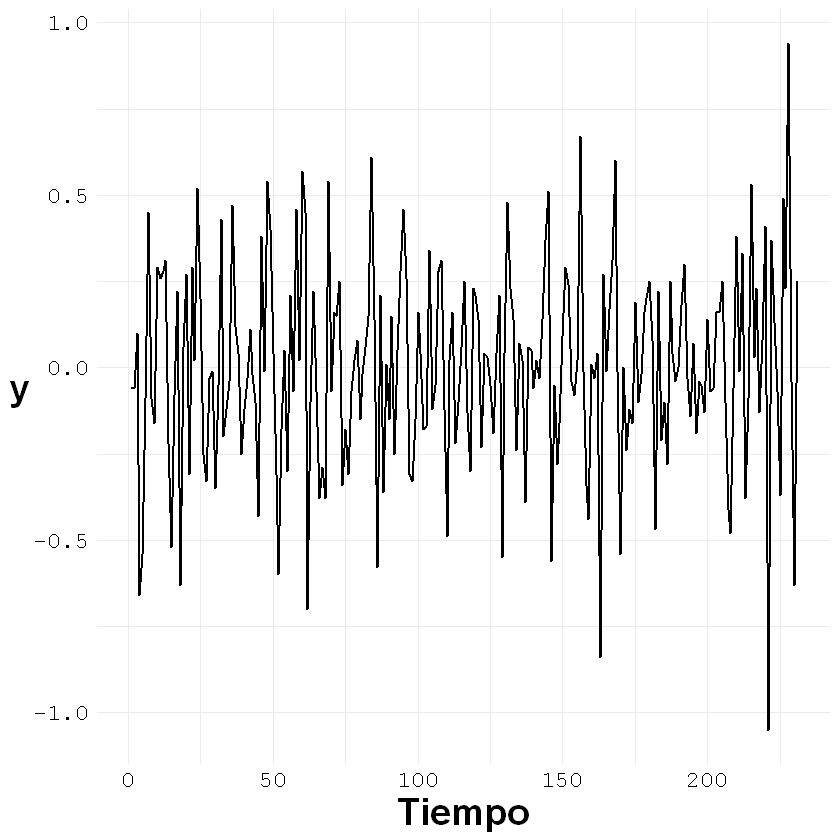
acf(z, type = "correlation", lag.max = 50)
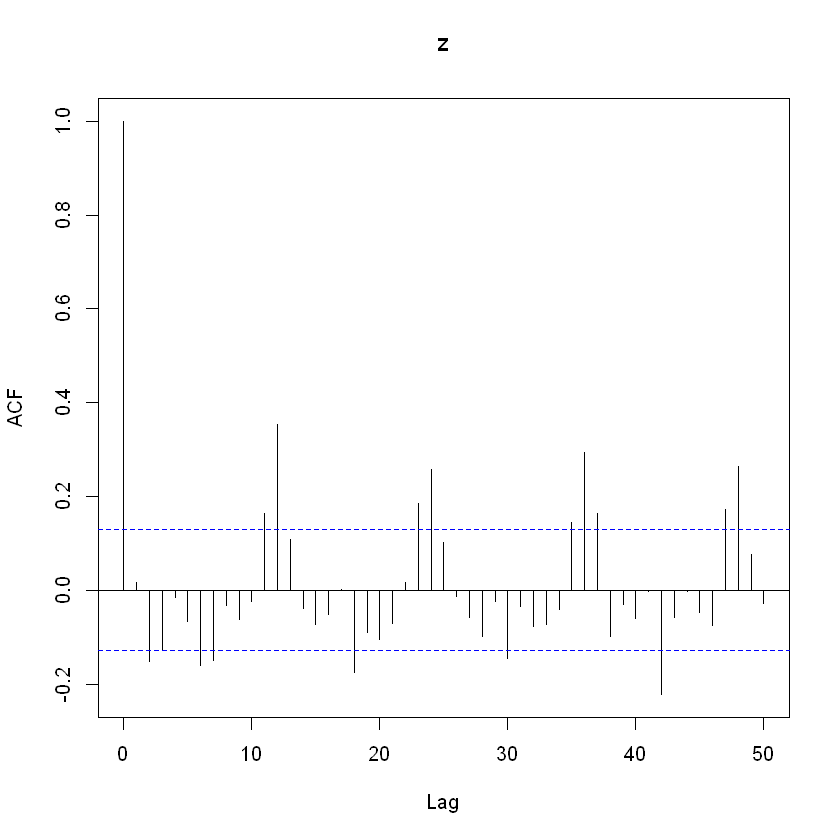
Diferencias de segundo orden:
z <- diff(y[,2], lag = 1, differences = 2)
z <- data.frame(z)
print(head(z))
z
1 -2.220446e-16
2 1.600000e-01
3 -7.600000e-01
4 1.200000e-01
5 4.500000e-01
6 5.400000e-01
ggplot()+geom_line(aes(x = c(1:nrow(z)), y = z[,1]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
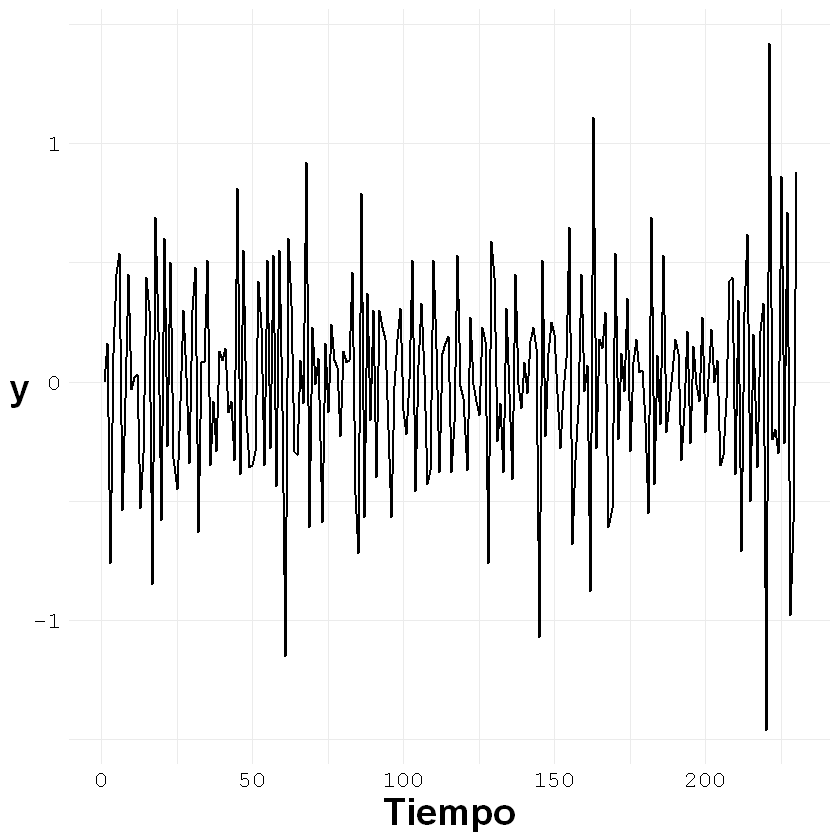
acf(z, type = "correlation", lag.max = 50)
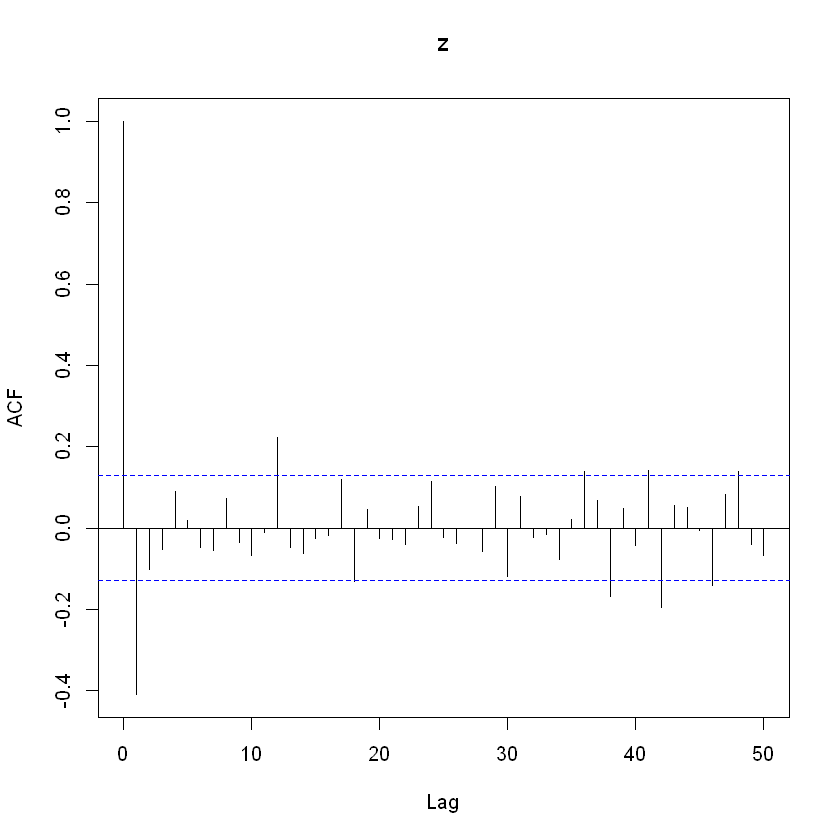
Ejemplo con el precio mensual del COLCAP:
Utilizar el archivo COLCAP.csv
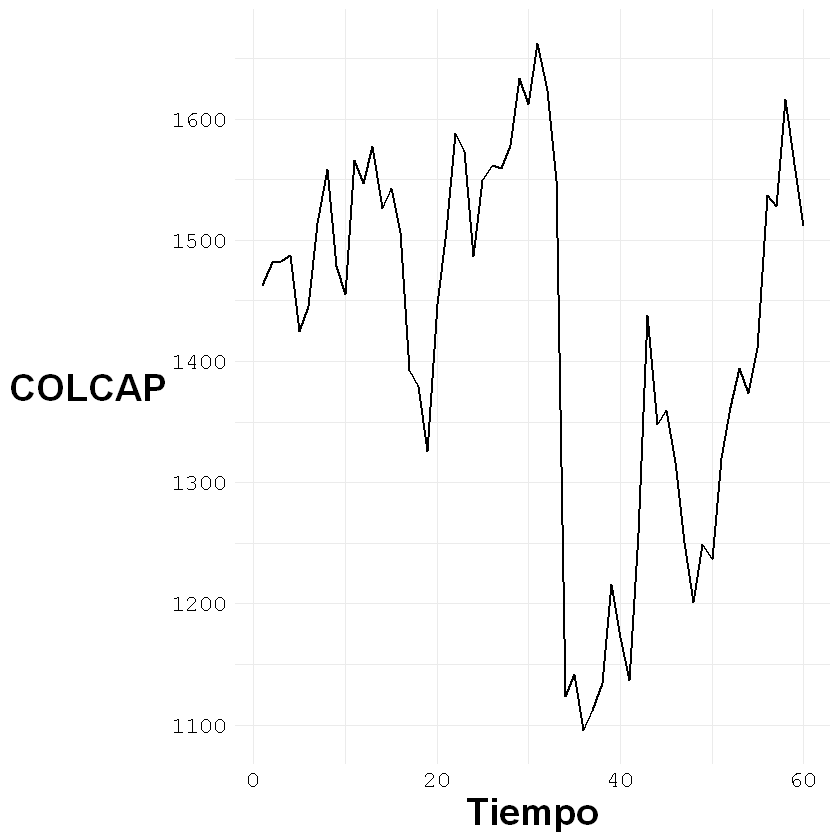
y <- read.csv("COLCAP.csv", sep = ";", dec = ",", header = T)
ggplot()+geom_line(aes(x = c(1:nrow(y)), y = y[,2]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "COLCAP")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
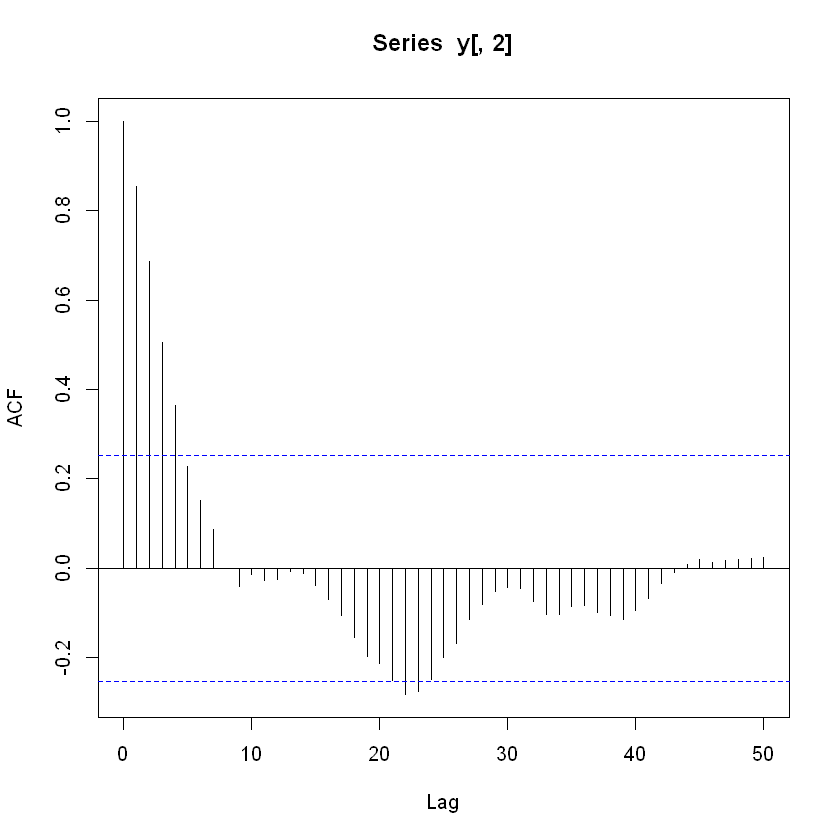
acf(y[,2], type = "correlation", lag.max = 50)
Diferencias de primer orden:
z <- diff(y[,2], lag = 1, differences = 1)
z <- data.frame(z)
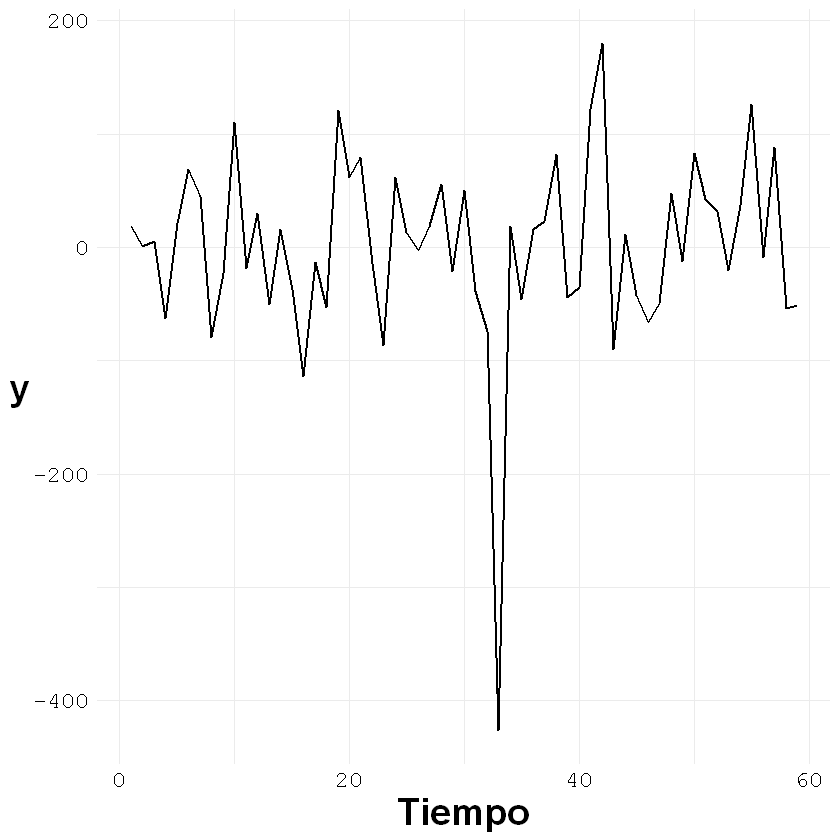
ggplot()+geom_line(aes(x = c(1:nrow(z)), y = z[,1]), size = 0.7)+
theme_minimal() +
labs(x = "Tiempo", y = "y")+
theme(axis.text = element_text(size = 14, family = 'mono', color = 'black'),
axis.title.x = element_text(face = "bold", colour = "black", size = rel(2)),
axis.title.y = element_text(face = "bold", colour = "black", size = rel(2), angle = 0,vjust = 0.5))
acf(z, type = "correlation", lag.max = 50)