Teoría Regresión Logística
Es un método de regresión para modelar variables categóricas, particularmente variables binarias también llamadas variables dicotómicas. La variable dependiente \(y\), solo puede tener dos valores: \(1\) o \(0\), lo que representa “si” y “no”. También podría indicarse “éxito” y “fracaso” o “verdadero” y “falso”. Estas asignaciones son arbitrarias a una característica cualitativa. El uso de la regresión logística clasifica las observaciones en estas dos categorías. Cada observación pertenece a la categoría 1 o a la categoría 0 dependiendo de la probabilidad estimada en el modelo. Por tanto, con la regresión logística no se predice si una observación es 1 o 0, sino la probabilidad de que se produzca la categoría de 1.
La variable respuesta \(y\), es una variable aleatoria Bernoulli con la siguiente distribución de probabilidad.
\(y = 1\): con una probabilidad, \(p\)
\(y = 0\): con una probabilidad, \(1 - p\)
El valor esperado de \(y\) es \(p\), es decir, el valor esperado es la probabilidad de que la variable \(y\) tenga el valor de 1.
Si \(y\) es binaria se cumple lo siguiente:
Los errores no son normales, tendrán lo siguintes dos valores:
\(\varepsilon = 1 - p\) cuando \(y = 1\).
\(\varepsilon = - p\) cuando \(y = 0\).
La varianza del error no es constante: \(\sigma^2_y = p (1-p)\)
La función para la variable respuesta \(y\) tiene la siguiente restricción: \(0 \leq p \leq 1\)
Como la variable respuesta \(y\) es binaria, se debe usar una función no lineal que podría ser creciente o decreciente y en forma de \(S\) o \(S\) invertida.
La función que más se usa es la logística:
O lo que es igual:
El objetivo del modelo de regresión logística binaria es estimar la probabilidad de que una variable \(y\) de dos categorías tome el valor de \(1\) (“si”) en lugar de \(0\) (“no”).
Al igual que en los modelos de regresión lineal, el modelo logístico incluye variables explicativas o regresoras que pueden ser continuas o variables indicadoras. La regresión logística binaria logra esto con la transformación de la ecuación de regresión mediante el uso de la función logística.
En el denominador de esta ecuación aparece la ecuación de regresión lineal, pero tiene una transformación. Con esta función se garantiza que los valores predichos ven entre cero y uno, tal como se supone que lo hacen las probabilidades.
Los modelos de regresión logística no utilizan los mínimos cuadrados para la estimación, lo hacen empleando la estimación por máxima verosimilitud.
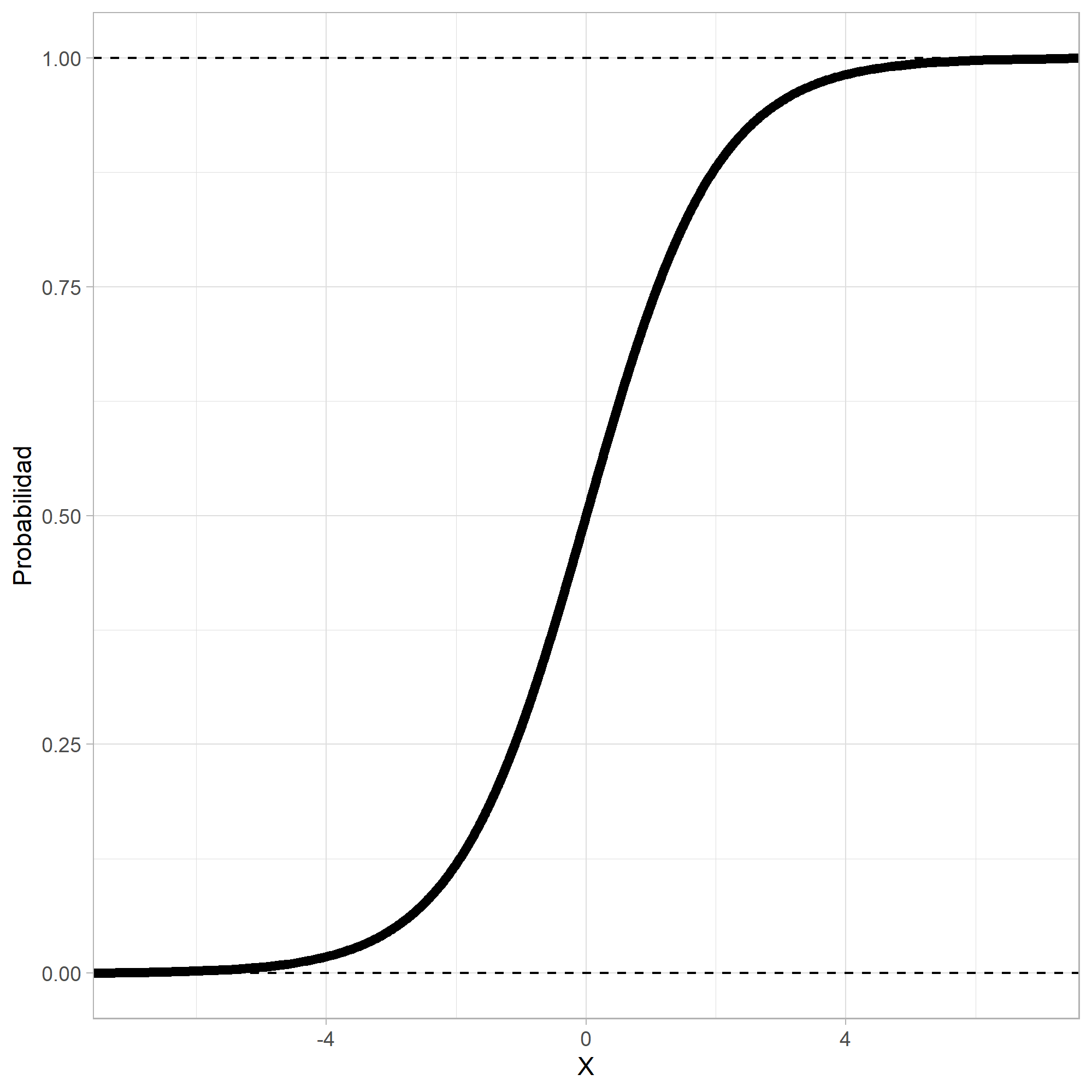
Sigmoide
Regression
La ecuación logística se puede linealizar de la siguiente manera:
A esta última ecuación que transforma la ecuación logística se llama transformación logit de la probabilidad \(p\).
La expresión anterior en inglés se llama odds ratio, en español no tenemos una traducción equivalente, pero a veces usan el término de ventaja, oportunidad y probabilidad. Se debe aclarar que no es una probabilidad.
Otra transformación con la misma forma que la función logística es la transformación probit, obtenida transformando \(p\) con la distribución normal acumulada; sin embargo, no se usa con frecuencia porque no puede incorporar con facilidad más de una variable regresora.
Asimetría de odd:
Supongamos una probabilidad de éxito del 10%, entonces la probabilidad de fracaso es del 90%, por lo tanto, odds ratio es igual a 0,111. Este resultado es menor a 1 porque es mayor la probabilidad de fracaso. En cambio, si la probabilidad de éxito es del 90% y la de fracaso el 10%, odds ratio es igual a 9, en otras palabras, se tiene una probabilidad de éxito de 9 a 1.
Si este resultado es mayor a 1 indica que el éxito es 9 veces mayor que el fracaso. Note que existe una asimetría en odds ratio: cuando la probabilidad de éxito es menor al 50%, el resultado se ubica entre el 0 y el 1, y con probabilidades mayores al 50%, odds ratio empieza en 1 y va hasta infinito.
print(0.1/(1-0.1))
print(0.2/(1-0.2))
print(0.3/(1-0.3))
print(0.4/(1-0.4))
print(0.5/(1-0.5))
print(0.6/(1-0.6))
print(0.7/(1-0.7))
print(0.8/(1-0.8))
print(0.9/(1-0.9))
[1] 0.1111111
[1] 0.25
[1] 0.4285714
[1] 0.6666667
[1] 1
[1] 1.5
[1] 2.333333
[1] 4
[1] 9
Simetría de log(odds ratio):
Con el \(log\) se transforma odds ratio y se convierte lineal. Note que con esta transformación se obtiene una asimetría.
print(log(0.1/(1-0.1)))
print(log(0.2/(1-0.2)))
print(log(0.3/(1-0.3)))
print(log(0.4/(1-0.4)))
print(log(0.5/(1-0.5)))
print(log(0.6/(1-0.6)))
print(log(0.7/(1-0.7)))
print(log(0.8/(1-0.8)))
print(log(0.9/(1-0.9)))
[1] -2.197225
[1] -1.386294
[1] -0.8472979
[1] -0.4054651
[1] 0
[1] 0.4054651
[1] 0.8472979
[1] 1.386294
[1] 2.197225
Interpretación de los coeficientes:
La interpretación de los coeficientes, \(\beta_j\), en la regresión logística es diferente que en los modelos de regresión lineal.
Como,
Exponencial a ambos lados:
Se deduce que para el modelo de regresión:
La interpretación de los coeficientes de hace como los odds ratio, así que se aplica exponencial a los resultados estimados. Para la variable regresora \(j\), odds ratio es igual a \(exp(\hat{\beta_j})\), este es el aumento estimado de la probabilidad de “éxito” \((y=1)\), asociado a un cambio unitario en el valor de la variable predictora \(X_j\), suponiendo que las demás variables son constantes.
Por ejemplo, un coeficiente estimado \(\hat{\beta}= 0,0935\), \(oddsRatio = exp(0,0935) = 1,10\). Esto implica que un aumento unitario en la variable \(X\), aumenta 10% la probabilidad de obtener “éxito”. Si la variable \(X\) aumenta 20 veces, \(oddsRatio = exp(20 \times 0,0935) = 6,5\), indica que las probabilidades aumentan 6,5 veces.
Si en este ejemplo el Beta es negativo, \(\hat{\beta}= -0,0935\), entonces odds ratio es menor que 1, en este caso es \(oddsRatio = exp(-0,0935) = 0,91\). Se interpreta que para un aumento unitario de la variable \(X\), la probabilidad disminuye un 9%.
Otra forma de interpretar los coeficientes es la siguiente:
Los coeficientes de la regresión logística se pueden interpretar con la diferencia porcentual.
Con la ecuación anterior podemos determinar el efecto que tienen los coeficientes Beta negativos sobre la variable resultado. Recuerde que a los coeficientes Beta se les aplican la función exponencial y está siempre toma valores positivos, pero con valores negativos, el resultado de la exponencial es menor que la unidad.
Si \(\beta_j\) es negativo entonces \(\left[ exp(\beta_j) -1 \right] \times 100\) es negativo. El resultado es el porcentaje que disminuye la variable \(y\), para un aumento en una unidad de la variable \(X_j\).
Si \(\beta_j\) es positivo entonces \(\left[ exp(\beta_j) -1 \right] \times 100\) es positivo. El resultado es el porcentaje que aumenta la variable \(y\), para un aumento en una unidad de la variable \(X_j\).
Significancia de los parámetros:
Se usa la inferencia de Wald.
Pruebas de hipótesis:
El estadístico para estas hipótesis es el estadístico z.
Estadístico z:
Este estadístico se distribuye como una normal, de ahí su nombre de z Score. En los modelos de regresión lineal se usa el estadístico t, pero para los odds ratio se usa el estadístico z. Los valores grandes de z indican una variable predictora significativa al modelo.
Para calcular el estadístico z primero se halla el error estándar para cada coeficiente, \(SE(\hat{\beta_j})\).
Errores estándar:
Los errores estándar permiten determinar si el coeficiente es significativamente diferente de 0. Un coeficiente de 0 indica que no hay efecto y no contribuye en nada a comprender la variable respuesta.
La diagonal de la matriz de varianzas-covarianzas de los errores son las
varianzas de los coeficientes. En R se calculan así:
diag(vcov(modelo_logit))
Así que la desviación estándar los errores es la raíz cuadrada:
sqrt(diag(vcov(modelo_logit)))
Valor p:
El valor p pone a prueba la hipótesis nula de que el valor del coeficiente asociado es cero. Cuanto menor sea el valor p, más probable de que \(\hat{\beta_j} \neq 0\). El nivel de significancia más usado es un \(\alpha=0,05\). Con valores p menores a \(\alpha\) indican que la variable predictora contribuye significativamente al modelo.
pvalue <- 2*pnorm(abs(zscore), lower.tail = FALSE)
Intervalos de confianza:
Un intervalo de confianza del 95% es:
coef - qnorm(.975) * se
coef + qnorm(.975) * se
Donde qnorm(.975) es igual a 1,959964.
Estos intervalos de confianza son para los coeficientes, los cuales son el exponente de odds ratio. También se llaman coeficientes de confianza de Wald.
Si el intervalo de confianza de un coeficiente incluye el 0, no podríamos estar significativamente seguros de que el coeficiente no es realmente 0. Para los odds ratio, dado que los intervalos de confianza son exponenciales de los intervalos de confianza de los coeficientes, si el rango incluye el 1, es evidencia de que la hipótesis nula no ha sido rechazada, el coeficiente no es significativo. Esto puede ocurrir hasta con valores p inferiores a \(\alpha\).
Ajuste del modelo:
El ajuste del modelo se hace comparando la desviación del modelo ajustado con la de un modelo saturado, que es un modelo con \(n\) parámetros y se ajusta perfectamente a los datos de la muestra. Esto lo hace con el logaritmo de la máxima verosimilitud de cada uno de estos dos modelos.
La diferencia entre estas dos desviaciones se aproxima a una distribución Chi-cuadrado, con \(n-k\) grados de libertad.
En la salida de R, la desviación del modelo saturado es
Null deviance y para el modelo ajustado es Residual deviance.
Al calcular el Chi-cuadrado se aplica el criterio del \(\alpha\) del valor p para la significancia, al igual que los modelos de regresión lineal.
Esta diferencia también se podría aplicar para comparar modelos, se realiza la diferencia entre la desviación estándar del modelo más simple con la desviación estándar del modelo completo. Si el resultado de la Chi-cuadrado de esta diferencia es significativo, entonces el modelo completo mejora la capacidad de predicción, de lo contrario, el modelo más simple es el mejor.
Como R no proporciona el valor p asociado, lo podemos calcular con
la función pchisq():
Significancia para el modelo:
pchisq(Null deviance - Residual deviance, df = k, lower.tail = FALSE)
Significancia para comparar modelos:
pchisq(Residual deviance Modelo 1 - Residual deviance Modelo 2, df = k, lower.tail = FALSE)
Para comparar modelos también se puede usar el criterio de información AIC. El modelo con el menor AIC es mejor y sería el que tendría mejor capacidad de predicción.
Resultados en R:
En R tenemos la función glm() de modelo lineal generalizado
(generalized linear model) para estimar los modelo logísticos binarios.
La distribución de la variable \(y\) se especifica con el argumento
family = binomial.
Para obtener los \(log-oddsRatio\) se aplica exponencial a los coeficientes estimados. Para los intervalos de confianza también se aplica exponencial al intervalo de confianza que calcula la función.
El modelo en R proporciona los valores de las desviaciones estándar
nulos, Null deviance y Residual deviance. También muestra el
AIC, pero no muestra la suma de los cuadrados (SSR y SSE), valores de
\(R^2\) y los estadísticos F.
El modelo lineal generalizado - GLM (generalized linear model) es la unificación de los modelos de regresión lineal y no lineal, que también permite incorporar distribuciones de la variable respuesta del tipo no Normal. En los GLM la distribución de la variable \(y\) solo es necesario que sea miembro de la familia exponencial, que comprende la distribuciones: normal, binomial, Poisson, entre otros. El método de la regresión logística hace parte de estos modelos lineales generalizados.
En la regresión logística no se asume relación lineal entre las variables regresoras, tampoco la homogeneidad de la varianza y no se supone que estas variables se distribuyan según una normal multivariada.