Regresión Logística en R
datos = read.csv("Social_Network_Ads.csv", sep = ",", dec = ".", header = T)
print(head(datos))
User.ID Gender Age EstimatedSalary Purchased
1 15624510 Male 19 19000 0
2 15810944 Male 35 20000 0
3 15668575 Female 26 43000 0
4 15603246 Female 27 57000 0
5 15804002 Male 19 76000 0
6 15728773 Male 27 58000 0
str(datos)
'data.frame': 400 obs. of 5 variables:
$ User.ID : int 15624510 15810944 15668575 15603246 15804002 15728773 15598044 15694829 15600575 15727311 ...
$ Gender : chr "Male" "Male" "Female" "Female" ...
$ Age : int 19 35 26 27 19 27 27 32 25 35 ...
$ EstimatedSalary: int 19000 20000 43000 57000 76000 58000 84000 150000 33000 65000 ...
$ Purchased : int 0 0 0 0 0 0 0 1 0 0 ...
Variables:
df <- datos[,c("Gender", "Age", "EstimatedSalary", "Purchased")]
print(head(df))
Gender Age EstimatedSalary Purchased
1 Male 19 19000 0
2 Male 35 20000 0
3 Female 26 43000 0
4 Female 27 57000 0
5 Male 19 76000 0
6 Male 27 58000 0
dim(df)
- 400
- 4
Variable y:
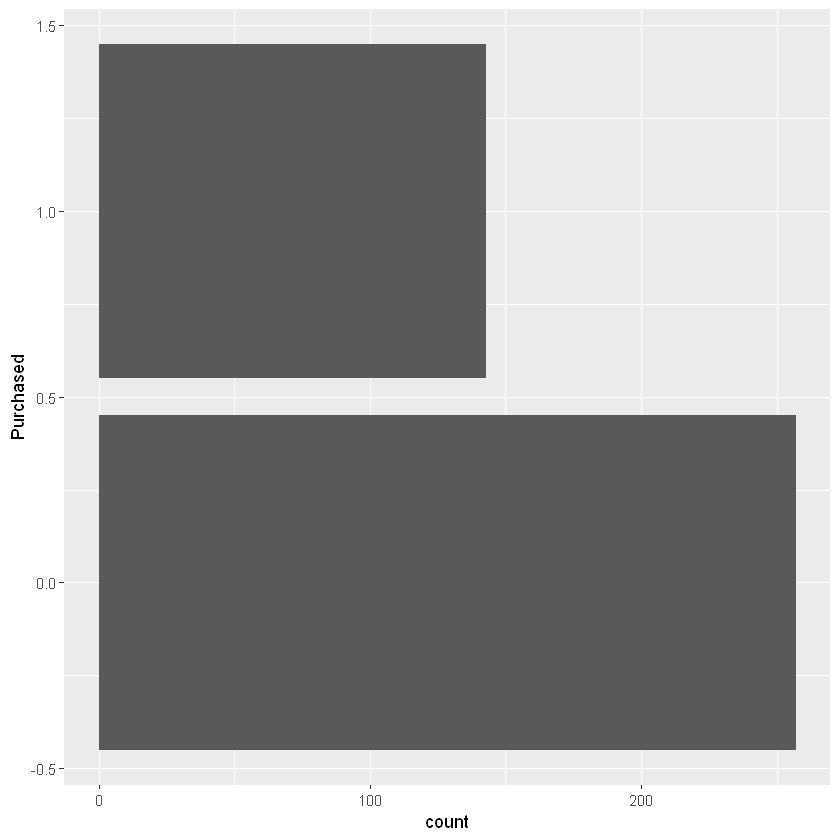
print(table(df[,c("Purchased")]))
0 1
257 143
print(table(df[,c("Purchased")])/nrow(df))
0 1
0.6425 0.3575
library(ggplot2)
ggplot(data = df) + geom_bar(aes(y = Purchased))
Variable categórica:
unique(df$Gender)
- 'Male'
- 'Female'
df$Gender <- factor(df$Gender,
levels = c(unique(df$Gender)),
labels = c(1,0))
print(head(df))
Gender Age EstimatedSalary Purchased
1 1 19 19000 0
2 1 35 20000 0
3 0 26 43000 0
4 0 27 57000 0
5 1 19 76000 0
6 1 27 58000 0
Ajuste modelo simple:
\[p = \frac{1}{1+exp \left[- \left(\beta_0+\beta_1 \times Edad \right)\right]}\]
logistic_simple <- glm(Purchased ~ Age, data = df, family = binomial)
logistic_simple
Call: glm(formula = Purchased ~ Age, family = binomial, data = df)
Coefficients:
(Intercept) Age
-8.0441 0.1889
Degrees of Freedom: 399 Total (i.e. Null); 398 Residual
Null Deviance: 521.6
Residual Deviance: 336.3 AIC: 340.3
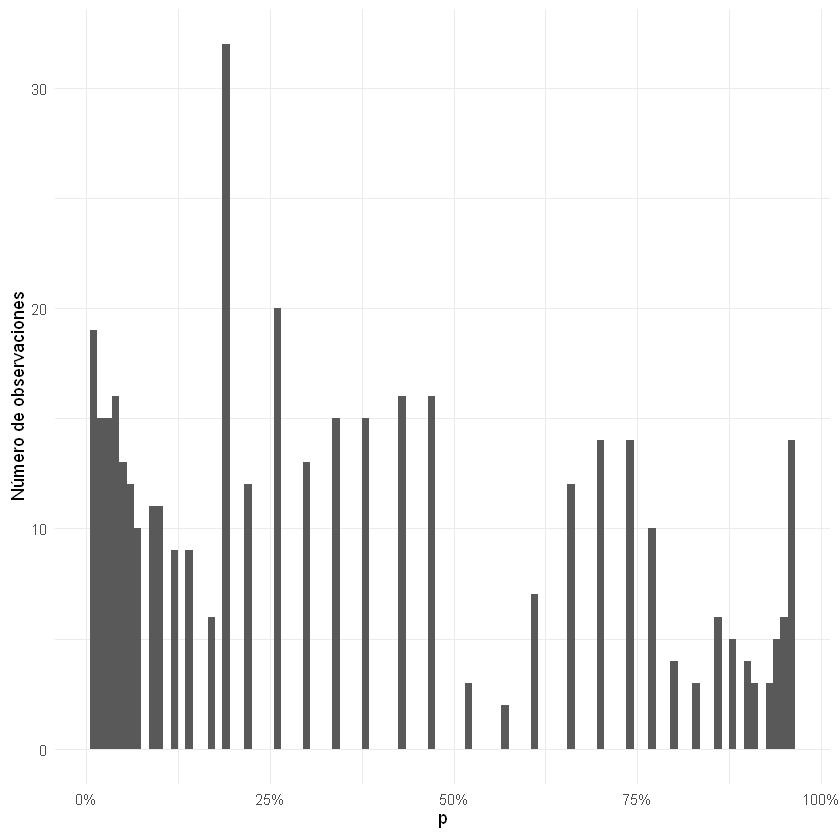
print(head(logistic_simple$fitted.values))
1 2 3 4 5 6
0.01149707 0.19295760 0.04182836 0.05009205 0.01149707 0.05009205
print(min(logistic_simple$fitted.values))
print(max(logistic_simple$fitted.values))
[1] 0.009536473
[1] 0.9641822
ggplot() + geom_histogram(aes(x = logistic_simple$fitted.values), binwidth = 0.01)+
scale_x_continuous(labels = scales::percent)+
labs(x = expression(p), y = "Número de observaciones")+
theme_minimal()
summary(logistic_simple)
Call:
glm(formula = Purchased ~ Age, family = binomial, data = df)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.5091 -0.6548 -0.2923 0.5706 2.4470
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -8.04414 0.78417 -10.258 <2e-16 *
Age 0.18895 0.01915 9.866 <2e-16 *
---
Signif. codes: 0 '*' 0.001 '' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 521.57 on 399 degrees of freedom
Residual deviance: 336.26 on 398 degrees of freedom
AIC: 340.26
Number of Fisher Scoring iterations: 5
Coeficientes:
coef <- logistic_simple$coefficients
print(coef)
(Intercept) Age
-8.0441425 0.1889496
\[exp \left( coeficientes \right) = \frac{p }{1-p } = oddsRatio\]
OR <- exp(coef) # Odds Ratio
print(OR)
(Intercept) Age
0.0003209765 1.2079800978
Por cada año de más, la probabilidad de comprar aumenta un 21% aproximadamente.
Grados de libertad:
gl <- logistic_simple$df.null - logistic_simple$df.residual
print(gl)
[1] 1
Diferencia de las desviaciones:
dif_residuos <- logistic_simple$null.deviance - logistic_simple$deviance
print(dif_residuos)
[1] 185.3117
Valor p para bondad de ajuste:
p_value <- pchisq(q = dif_residuos, df = gl, lower.tail = FALSE)
print(p_value)
[1] 3.3555e-42
Se rechaza la hipótesis nula, entonces el modelo es significativo a un \(\alpha = 0,05\).
Error estándar:
\[SE(\hat{\beta_j})\]
SE <- sqrt(diag(vcov(logistic_simple)))[2]
print(SE)
Age
0.01915181
Estadístico z:
\[zScore = \frac{\hat{\beta_j}}{SE(\hat{\beta_j})}\]
zscore <- coef[2]/SE
print(zscore)
Age
9.865891
Valor p para el coeficiente:
p_value <- 2*pnorm(abs(zscore), lower.tail = FALSE)
print(p_value)
Age
5.85129e-23
El coeficiente Edad es significativo.
Predicción:
predict(logistic_simple, newdata = data.frame(Age = 33))
\[p = \frac{exp \left(\beta_0+\beta_1 \right)}{1 + exp \left(\beta_0+\beta_1 \times X_1 \right)}\]
exp(predict(logistic_simple, data.frame(Age = 33)))/(1+exp(predict(logistic_simple, data.frame(Age = 33))))
\[p = \frac{1}{1+exp \left[- \left(\beta_0+\beta_1 \times X_1 \right) \right]}\]
1/(1+exp(-predict(logistic_simple, data.frame(Age = 33))))
Ajuste modelo múltiple:
\[p = \frac{1}{1+exp \left[- \left(\beta_0+\beta_1 \times Género +\beta_2 \times Edad + \beta_3 \times Salario \right)\right]}\]
logistic <- glm(Purchased ~ Gender + Age + EstimatedSalary, data = df, family = binomial)
logistic
Call: glm(formula = Purchased ~ Gender + Age + EstimatedSalary, family = binomial,
data = df)
Coefficients:
(Intercept) Gender0 Age EstimatedSalary
-1.245e+01 -3.338e-01 2.370e-01 3.644e-05
Degrees of Freedom: 399 Total (i.e. Null); 396 Residual
Null Deviance: 521.6
Residual Deviance: 275.8 AIC: 283.8
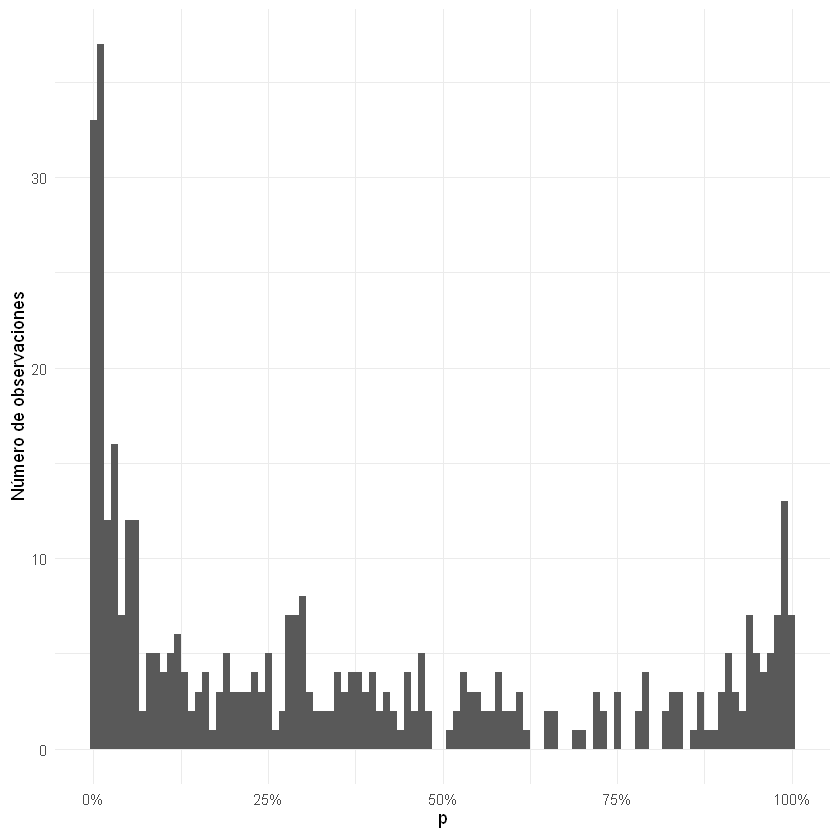
print(head(logistic$fitted.values))
1 2 3 4 5 6
0.0007061408 0.0314610656 0.0063340671 0.0132775722 0.0056085336 0.0191141370
print(min(logistic$fitted.values))
print(max(logistic$fitted.values))
[1] 0.0005440362
[1] 0.9988217
ggplot() + geom_histogram(aes(x = logistic$fitted.values), binwidth = 0.01)+
scale_x_continuous(labels = scales::percent)+
labs(x = expression(p), y = "Número de observaciones")+
theme_minimal()
summary(logistic)
Call:
glm(formula = Purchased ~ Gender + Age + EstimatedSalary, family = binomial,
data = df)
Deviance Residuals:
Min 1Q Median 3Q Max
-2.9109 -0.5218 -0.1406 0.3662 2.4254
Coefficients:
Estimate Std. Error z value Pr(>|z|)
(Intercept) -1.245e+01 1.309e+00 -9.510 < 2e-16 *
Gender0 -3.338e-01 3.052e-01 -1.094 0.274
Age 2.370e-01 2.638e-02 8.984 < 2e-16 *
EstimatedSalary 3.644e-05 5.473e-06 6.659 2.77e-11 *
---
Signif. codes: 0 '*' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
(Dispersion parameter for binomial family taken to be 1)
Null deviance: 521.57 on 399 degrees of freedom
Residual deviance: 275.84 on 396 degrees of freedom
AIC: 283.84
Number of Fisher Scoring iterations: 6
Coeficientes:
coef <- logistic$coefficients
print(coef)
(Intercept) Gender0 Age EstimatedSalary
-1.244979e+01 -3.338434e-01 2.369694e-01 3.644119e-05
\[exp \left( coeficientes \right) = \frac{p }{1-p } = oddsRatio\]
OR <- exp(coef) # Odds Ratio
print(OR)
(Intercept) Gender0 Age EstimatedSalary
3.918543e-06 7.161659e-01 1.267402e+00 1.000036e+00
Por cada año de más, la probabilidad de comprar aumenta un 27% aproximadamente, si las demás variables permanecen constantes.
Male = 1
Female = 0
Comparando entre hombres y mujeres, los hombres aumentan la probabilidad de compra aproximadamente 7 veces, si las demás variables permanecen constantes.
Un aumento en el salario no aumenta ni disminuye la probabilidad de compra.
Grados de libertad:
gl <- logistic$df.null - logistic$df.residual
print(gl)
[1] 3
Diferencia de las desviaciones:
dif_residuos <- logistic$null.deviance - logistic$deviance
print(dif_residuos)
[1] 245.7297
Valor p para bondad de ajuste:
p_value <- pchisq(q = dif_residuos, df = gl, lower.tail = FALSE)
print(p_value)
[1] 5.487701e-53
Se rechaza la hipótesis nula, entonces el modelo es significativo a un \(\alpha = 0,05\), pero existen unos coeficientes no significativos.
Error estándar:
\[SE(\hat{\beta_j})\]
SE <- sqrt(diag(vcov(logistic)))[2:4]
print(SE)
Gender0 Age EstimatedSalary
3.052264e-01 2.637705e-02 5.472858e-06
Estadístico z:
\[zScore = \frac{\hat{\beta_j}}{SE(\hat{\beta_j})}\]
zscore <- coef[2:4]/SE
print(zscore)
Gender0 Age EstimatedSalary
-1.093757 8.983922 6.658530
Valor p para el coeficiente:
p_value <- 2*pnorm(abs(zscore), lower.tail = FALSE)
print(p_value)
Gender0 Age EstimatedSalary
2.740618e-01 2.612829e-19 2.765798e-11
Género no es significativo. Edad y salario si son significativos.
Predicción:
predict(logistic, newdata = data.frame(Gender = '0', Age = 33, EstimatedSalary = 42000))
\[p = \frac{1}{1+exp \left[- \left(\beta_0+\beta_1 \times X_1 + ... + \beta_k \times X_k \right) \right]}\]
1/(1+exp(-predict(logistic, newdata = data.frame(Gender = '0', Age = 33, EstimatedSalary = 42000))))
Si se agrega el argumento type = "response" en la función
predict() el resultados son las probabilidades \(p\) y lugar los
𝑙𝑜𝑔(𝑜𝑑𝑑𝑠𝑅𝑎𝑡𝑖𝑜).
predict(logistic, newdata = data.frame(Gender = '0', Age = 33, EstimatedSalary = 42000), type = "response")