K-Means en R

Importar datos:

datos <- read.csv("EAM_2019-v2.csv", sep = ";", dec = ",", header = T)
print(head(datos))

  ï..gasto_personal inversion_AF    ventas
        32334949     92544622 321070109
         5669798     69317638  86597330
        11081213     50853587  26727389
        47892609     42426113 388005721
        56410101     35164028 390070138
        20536798     27028346 490639882

dim(datos)

216
3

str(datos)

'data.frame':       216 obs. of  3 variables:
 $ ï..gasto_personal: int  32334949 5669798 11081213 47892609 56410101 20536798 14001910 38533922 21397321 3478034 ...
 $ inversion_AF     : int  92544622 69317638 50853587 42426113 35164028 27028346 25150313 23019658 22007282 21924323 ...
 $ ventas           : int  321070109 86597330 26727389 388005721 390070138 490639882 379365700 488079500 233432780 9932602 ...

colnames(datos) <- c("Gasto_personal", "Inversión_AF", "Ventas")

Creamos una variable para almacenar solo las variables que queremos analizar.

df <- datos[, c("Gasto_personal", "Ventas")]

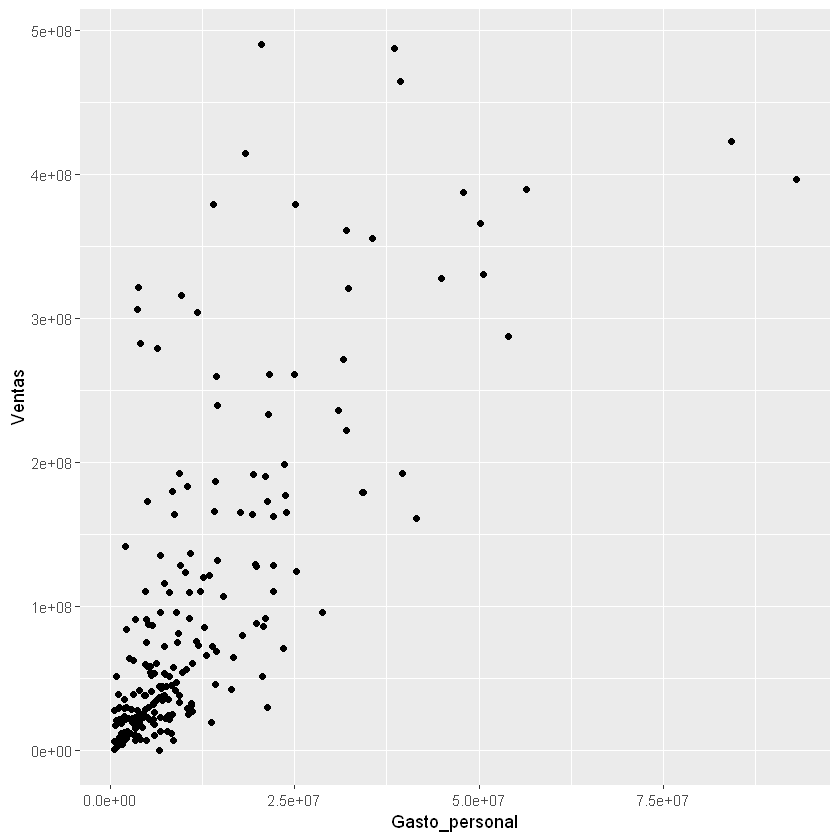
Dispersión de los datos:

library(ggplot2)

ggplot(data = df)+
    geom_point(aes(x = Gasto_personal, y = Ventas))

Escalamiento de variables:

Para Normalizar usaremos la función scale().

\[Normalización = X_{norm} = \frac{x_i-\overline{x}}{\sigma_x}\]

df_scaled <- scale(df)
df_scaled <- data.frame(df_scaled)  # Data Frame para ggplot2
print(head(df_scaled))

  Gasto_personal     Ventas
   1.52915807  1.9822451
  -0.47700945 -0.1241207
  -0.06987862 -0.6619571
   2.69964731  2.5835553
   3.34046558  2.6021008
   0.64151759  3.5055604

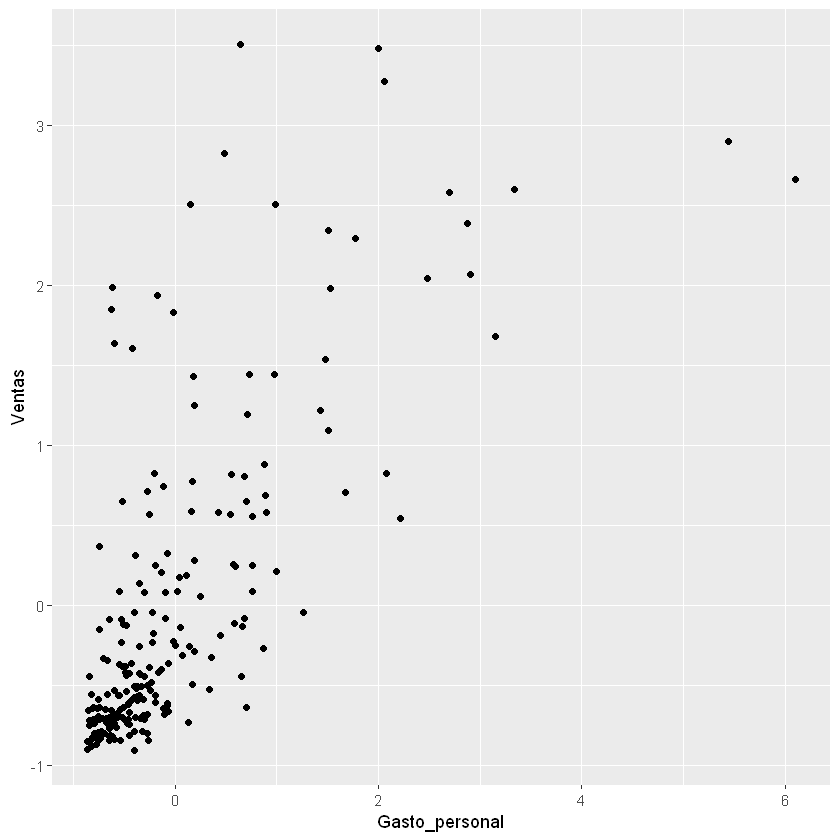
Dispersión de los datos escalados:

ggplot(data = df_scaled)+
    geom_point(aes(x = Gasto_personal, y = Ventas))

Distancia Euclideana:

\[D_1(x_i, x_j) =\sqrt{\sum_{k=1}^p{(x_{ix}-x_{jx})^2}}\]

Con la función dist() podemos calcular diferentes distancias con el argumento method =: "euclidean", "manhattan", "minkowski", entre otros. Cuando se usa la distancia "minkowski" se debe agregar el argumento p =.

dist_eucl <- dist(df_scaled, method = "euclidean")

Matriz de distancias:

De forma matricial se muestran las distancias entre todas las observaciones. La diagonal es cero porque es la distancia entre cada observación con ella misma.

Por ejemplo: la distancia Euclidiana entre la observación uno y dos es 2,9. Resta al cuadrado de la fila 1 con la fila 2 y el resultado se saca raíz cuadrada así:

print(sqrt((df_scaled[1,1]-df_scaled[2,1])^2+(df_scaled[1,2]-df_scaled[2,2])^2))

[1] 2.908863

Se sacará la matriz para las distancias entre las primeras 10 observaciones.

print(round(as.matrix(dist_eucl)[1:10, 1:10], 1))

 2   3   4   5   6   7   8   9  10
0.0 2.9 3.1 1.3 1.9 1.8 1.5 1.6 1.1 3.5
2.9 0.0 0.7 4.2 4.7 3.8 2.7 4.4 1.8 0.7
3.1 0.7 0.0 4.3 4.7 4.2 3.2 4.6 2.0 0.6
1.3 4.2 4.3 0.0 0.6 2.3 2.6 1.1 2.4 4.8
1.9 4.7 4.7 0.6 0.0 2.8 3.2 1.6 3.0 5.2
1.8 3.8 4.2 2.3 2.8 0.0 1.1 1.4 2.3 4.5
1.5 2.7 3.2 2.6 3.2 1.1 0.0 2.1 1.4 3.4
1.6 4.4 4.6 1.1 1.6 1.4 2.1 0.0 2.6 5.0
1.1 1.8 2.0 2.4 3.0 2.3 1.4 2.6 0.0 2.4
3.5 0.7 0.6 4.8 5.2 4.5 3.4 5.0 2.4 0.0

K-Means:

La función más usada es kmeans() de la librería stats.

Instalar el siguiente paquete: install.packages("stats")

sintaxis: kmeans(x, centers, iter.max = 10, nstart = 1)

x: Data Frame con los datos, agregaremos las distancias calculadas con dist().

centers: son los \(k\) clusters iniciales.

iter.max: número máximo de iteraciones. Por defecto es 10.

nstart: número de particiones iniciales aleatorias cuando centers es un número. Probar con nstart > 1

set.seed(1) # valor semilla para obtener siempre los mismos resultados.

names(kmeans(dist_eucl, 10))

'cluster'
'centers'
'totss'
'withinss'
'tot.withinss'
'betweenss'
'size'
'iter'
'ifault'

cluster: un vector de enteros (desde 1:k) que indica el cluster al que se asigna cada punto.

centers: una matriz con los centroides.

withinss: vector con los WCSS de cada cluster. El resultado es después de definir la cantidad de clusters.

size: cantidad de puntos en cada cluster.

Número óptimo de clusters:

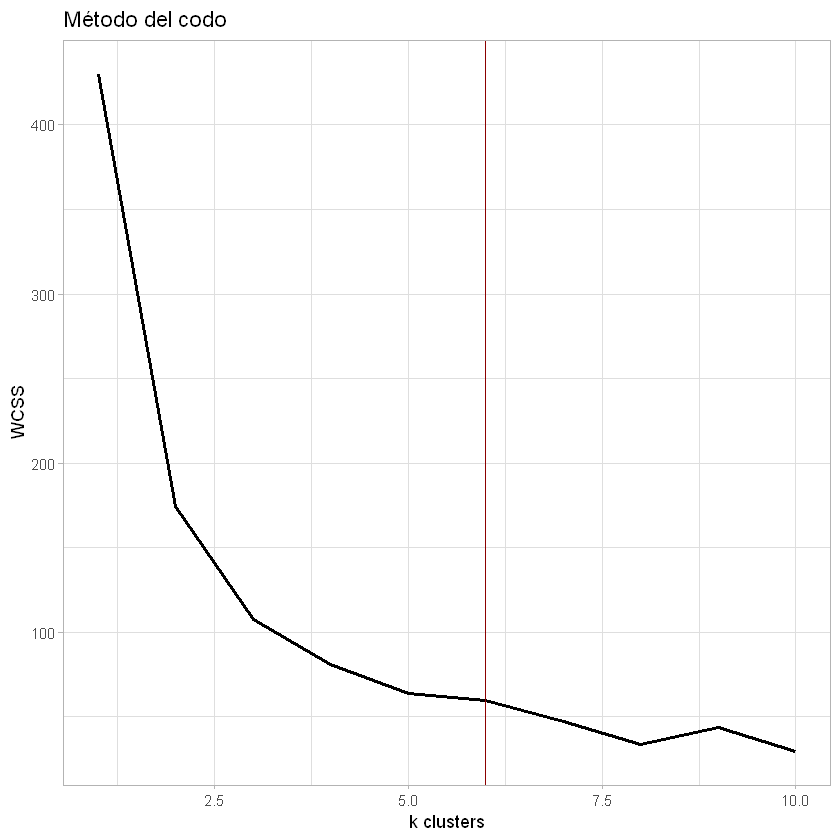
Método del codo:

Se calculará el valor de WCSS aplicando K-Means aumentando la cantidad de centroides.

wcss = vector()
for (i in 1:10){
  wcss[i] <- sum(kmeans(df_scaled, i)$withinss)
}
ggplot()+geom_line(aes(x = c(1:10), y = wcss), size = 1)+
    geom_vline(xintercept  = 6, color = "darkred")+
    labs(title = "Método del codo",
         x = "k clusters",
         y = "WCSS")+
    theme_light()

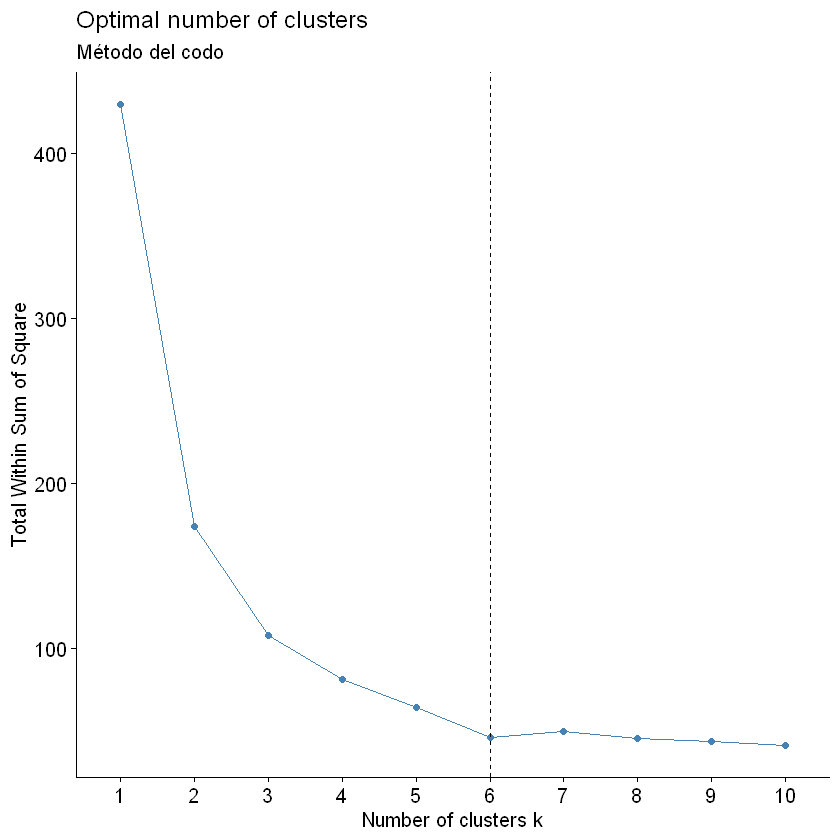
Este método también lo podemos hacer con la función fviz_nbclust() del paquete factoextra.

install.packages("factoextra")

library(factoextra)

Warning message:
"package 'factoextra' was built under R version 4.1.3"
Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa

fviz_nbclust(df_scaled, kmeans, method = "wss") +
    geom_vline(xintercept = 6, linetype = 2)+
    labs(subtitle = "Método del codo")

Método de la silueta:

Este método también lo hacemos con la función fviz_nbclust()

fviz_nbclust(df_scaled, kmeans, method = "silhouette")+
    labs(subtitle = "Método de la silueta")

Método del gap estadístico:

fviz_nbclust(df_scaled, kmeans, method = "gap_stat")+
    labs(subtitle = "Gap statistic method")

Aplicación del K-Means con k óptimo:

\(k = 3\):

Recomiendo llamar el modelo de cualquier forma diferente a kmeans por este nombre se utiliza para algunas librerías como función y no como una variable; por ejemplo, guardemos el resultado con el nombre de k_means.

k_means <- kmeans(dist_eucl, 3, iter.max = 300, nstart = 10)

Cantidad de observaciones por cada cluster:

¿Cómo cambia este resultado para 3 clusters?

print(k_means$size)

[1]  15  46 155

Para visualizar los clusters en los datos originales usaremos la función clusplot() del paquete cluster.

Instalar el paquete: install.packages("cluster")

library(cluster)

Warning message:
"package 'cluster' was built under R version 4.1.3"

clusplot(df,
         k_means$cluster,       # el cluster que se le asigna a cada punto.
         lines = 0,            # para eliminar líneas en el gráfico.
         labels = 4,           # 4 para que ponga una etiqueta al número del cluster.
         color = TRUE,         # diferente colo para cada sector.
         plotchar = FALSE,     # con FALSE se quitan los símbolos diferentes para cada cluster.
         span = TRUE,          # TRUE para que represente el cluster con una elipse no como círculo.
         main = "Clustering de empresas",
         xlab = "Activos Totales",
         ylab = "Ingresos Operacionales"
         )

Otra forma de visualizar los cluster con fviz_cluster()

fviz_cluster(k_means, data = df,
             stand = FALSE,            # FALSE para que no estandarice los datos, ya se había hecho esto.
             show.clust.cent = TRUE,   # TRUE para que muestre los centroides.
             ellipse = TRUE,              # Puede ser FALSE o TRUE
             ggtheme = theme_minimal())

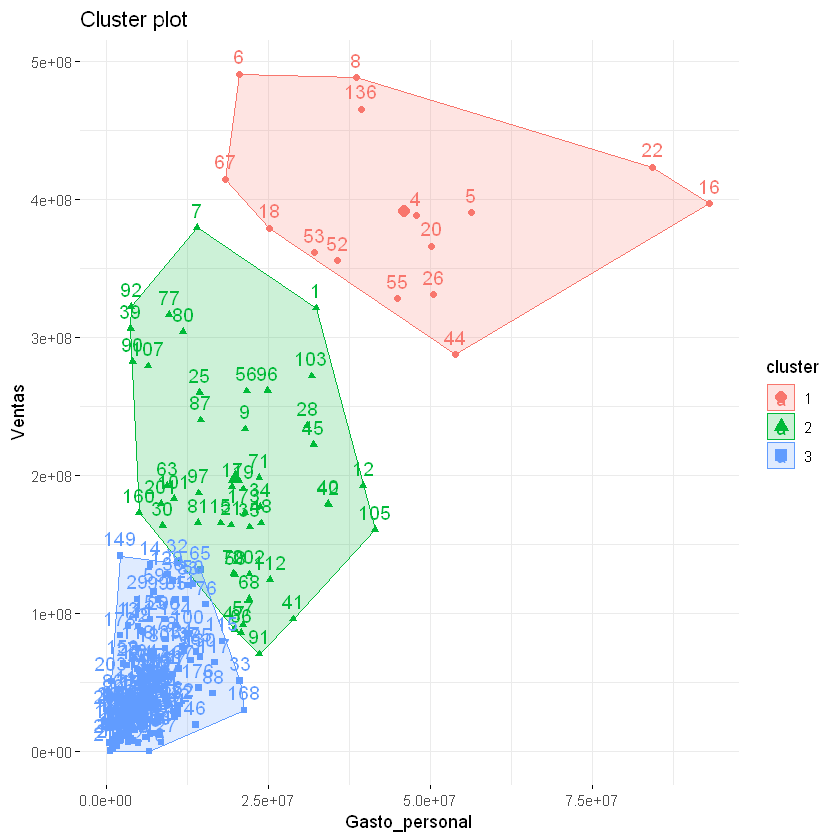
Es posible calcular la media de cada variable por cluster utilizando los datos originales:

print(aggregate(df, by = list(cluster = k_means$cluster), mean))

  cluster Gasto_personal    Ventas
     1       46055433 390956062
     2       19831448 197627597
     3        6394092  43446519

\(k = 6\):

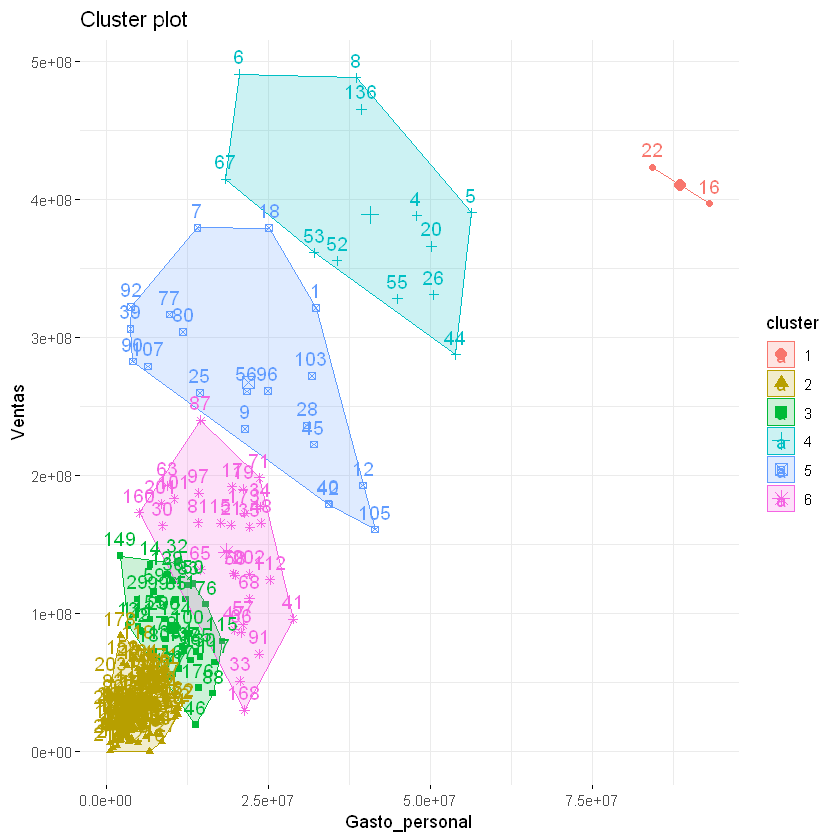
k_means <- kmeans(dist_eucl, 6, iter.max = 300, nstart = 10)
print(k_means$size)

[1]   2 115  37  12  20  30

fviz_cluster(k_means, data = df,
             stand = FALSE,            # FALSE para que no estandarice los datos, ya se había hecho esto.
             show.clust.cent = TRUE,   # TRUE para que muestre los centroides.
             ellipse = TRUE,              # Puede ser FALSE o TRUE
             ggtheme = theme_minimal())

Realizar el K-Means con distancias Manhattan y Minkowski con p igual 0.1, 0.5, 3 y 4.

Realizar lo anterior, pero sin estandarizar las variables

¿Para este caso en específico será necesario la estandarización de variables?

Realizar el K-Means con las siguientes variables: Inversión en AF y Ventas