Clusters Jerárquicos

El clúster jerárquico es un enfoque alternativo que agrupa objetos basado en su similaridad.

Una desventaja potencial del agrupamiento de K-means es que requiere que especifiquemos previamente el número de agrupamientos \(K\).

Es útil cuando los datos se observaron sin etiquetas de clase y que queremos realizar un agrupamiento pero no sabemos en cuantos clúster.

El clúster jerárquico, puede ser subdividido en 2 tipos:

1. Aglomerativo: cada observación se considera inicialmente como un grupo (hojas y ramas). Luego, los clústeres más similares se fusionan sucesivamente hasta que solo queda un solo clúster grande (raíz).

2. Divisivo: es un proceso inverso al agrupamiento aglomerativo, comienza con la raíz, en la que todos los objetos están incluidos en un grupo. Luego, los grupos más heterogéneos se dividen sucesivamente hasta que todas las observaciones están en su propio grupo.

El agrupamiento jerárquico no requiere una elección particular de \(K\). Otra ventaja es que brinda como resultado una atractiva representación basada en árboles, conocido como dendograma.

Aglomerativo:

El agrupamiento aglomerativo funciona “de abajo hacia arriba”. Es decir, cada objeto se considera inicialmente como un grupo de un solo elemento (similar a una hoja de un árbol). En cada paso del algoritmo, los dos grupos que son más similares se combinan en un nuevo grupo más grande (nodos). Este procedimiento se repite hasta que todos los puntos son miembros de un solo grupo grande (raíz).

Tenga en cuenta que el agrupamiento aglomerativo es bueno para identificar pequeños grupos. El agrupamiento divisivo es bueno para identificar grandes grupos. En este artículo, nos centraremos principalmente en el agrupamiento jerárquico aglomerativo.

Dendograma

Pasos para el algoritmo aglomerativo:

1. Preparación de los datos.

2. Cálculo de información de (des)similitud entre cada par de objetos en el conjunto de datos.

3. Uso de la función de vinculación para agrupar objetos en un árbol de clúster jerárquico, en función de la información de distancia generada en el paso 1. Los objetos/agrupaciones que están muy cerca se vinculan mediante la función de vinculación.

4. Determinar dónde cortar el árbol jerárquico en grupos. Esto crea una partición de los datos.

En la siguiente imagen se visualizan los pasos:

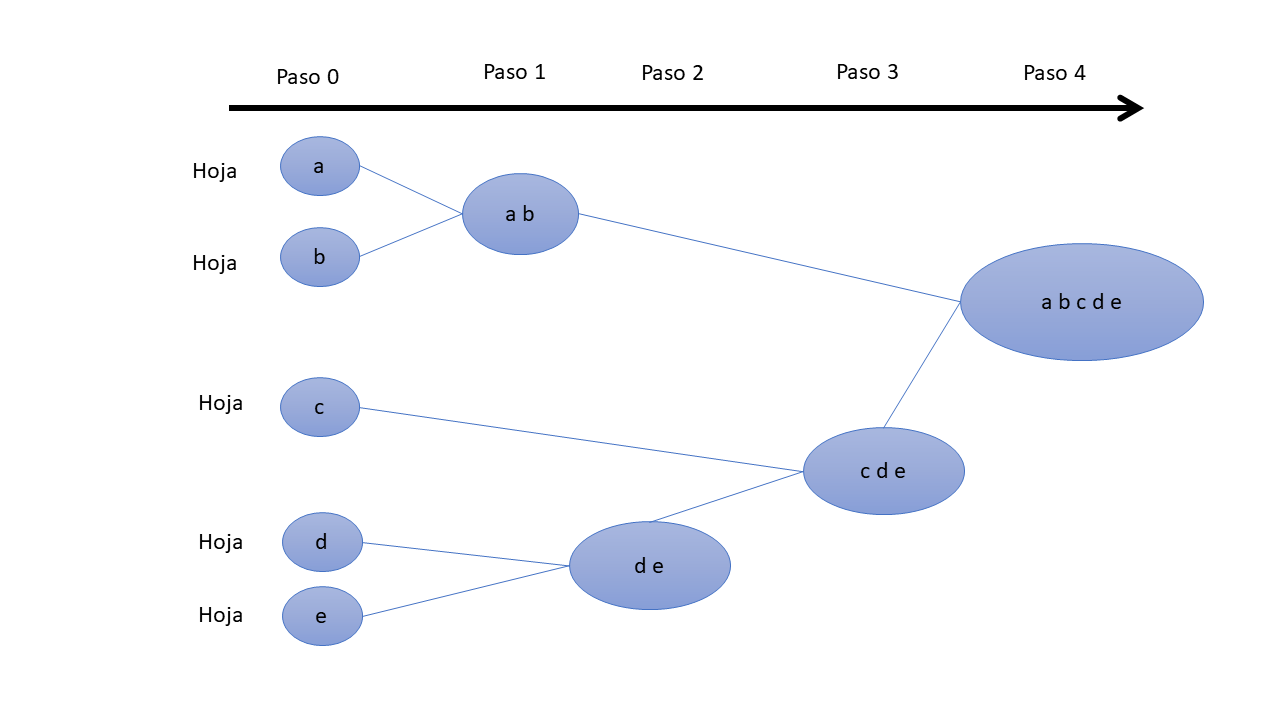
Pasos

Medidas de Similitud

Para decidir qué grupos u objetos combinarse o dividirse, necesitamos métodos para medir la similitud entre los objetos.

Existen muchos métodos para calcular la información de (des)similitud, puede usar la función dist() de R para calcular la distancia entre cada par de objetos en un conjunto de datos. Los resultados de este cálculo se conocen como matriz de distancia o disimilitud.

Vinculación de objetos o grupos

La función de vinculación toma la información de distancia, devuelta por la función dist(), y agrupa pares de objetos en grupos en función de su similitud. luego, estos grupos recién formados se vinculan entre sí para crear grupos más grandes. Este proceso se repite hasta que todos los objetos del conjunto de datos original se vinculan en un árbol jerárquico.

Veamos un ejemplo:

¿Cual es el dendograma resultante?

variable_1 = c(58,61,51,67,26,50,31,63,25,61)
variable_2 = c(5,1,6,3,3,2,8,7,0,15)
datos = cbind(variable_1, variable_2)
datos = data.frame(datos)

puntos = c("P1","P2","P3","P4","P5","P6","P7","P8","P9","P10")

library(ggplot2)

ggplot(data = datos)+geom_point(aes(x = variable_1, y = variable_2), size = 3)+theme_light()+
    labs(x = "Variable 1",
        y = "Variable 2")+
    geom_text(aes(x = variable_1, y = variable_2, label = puntos), nudge_x=-1, nudge_y=0.5, size = 5)

plot(hclust(dist(datos, method = "euclidean"), method = "ward.D"))

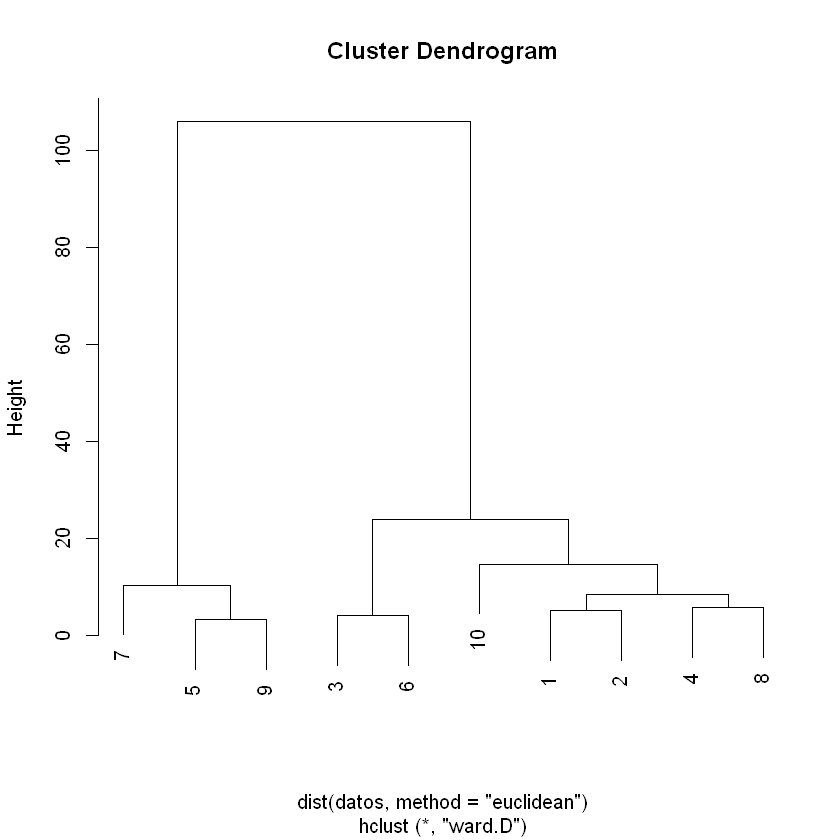
Los dendogramas corresponden a la representación gráfica del árbol jerárquico generado por la función hclust().

El dendograma se puede producir en R usando la función base plot(), de la salida de hclust(). Sin embargo también podemos usar la función fviz_dend() para producir dendrograma mas estético.

Verificar el árbol de Agrupamiento

Después de dibujado el árbol de clúster jerárquico, es posible que desee evaluar que las distancias (las alturas) en el árbol reflejen las distancias originales.

Una forma de medir qué tan bien el árbol de clústeres generado por la función hclust() refleja sus datos, es calcular la correlación entre las distancias cofenéticas y los datos de distancia originales generados por la función dist().

Si la agrupación es válida, la vinculación de objetos en el árbol de agrupación debería tener una fuerte correlación con las distancias entre objetos en la matriz de distancia original.

Cortar el dendograma para identificar el número de agrupaciones

Realmente no hay un criterio claro para cortar el dendograma, pueden incluso usarse las mismas medidas que el K-means. pero además, podrían usarse un numero de clústers definidos a priori o establecer un nivel máximo de desimilitud aceptada.

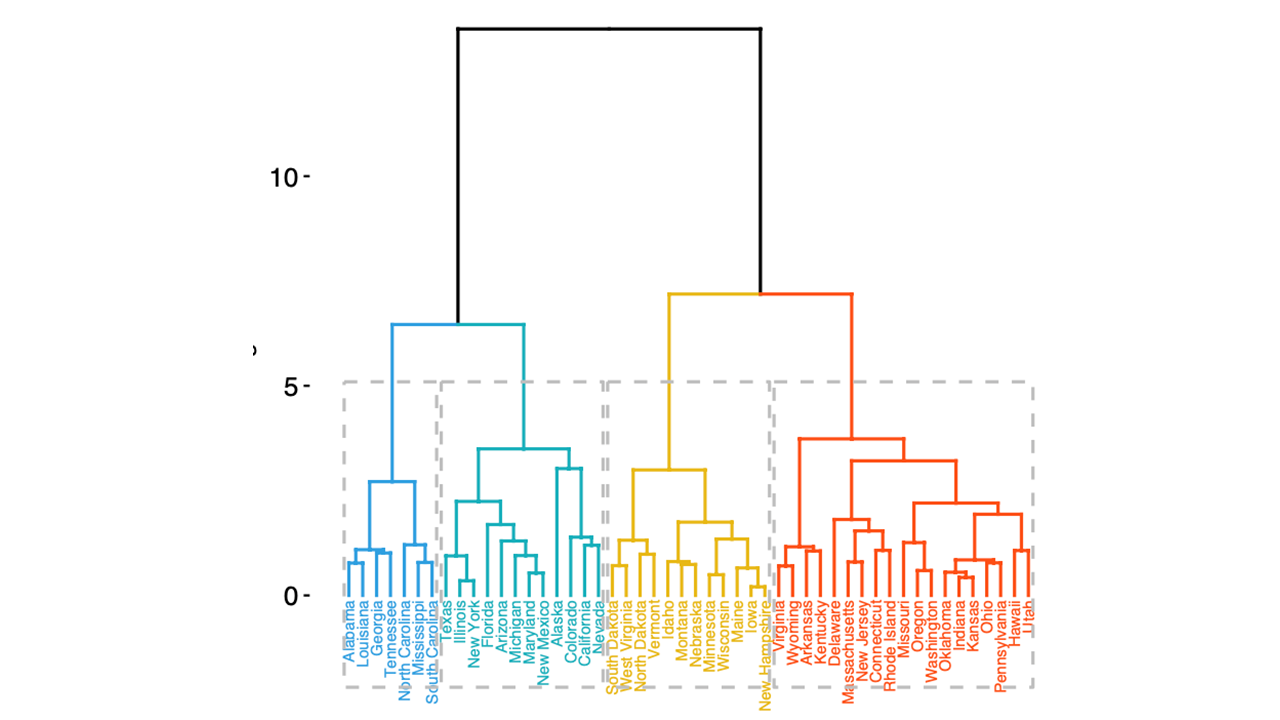
Dendograma_cortado