Análisis de correspondencias
Es una técnica gráfica para representar la información en una tabla de contingencia de doble entrada, que contiene los recuentos (frecuencias) de elementos para una clasificación cruzada de dos variables categóricas. Con el análisis de correspondencia, se construye una gráfica que muestra la interacción de las dos variables categóricas junto con la relación de las filas entre sí y de las columnas entre sí.
Ventajas:
Pueden representar relaciones entre filas y columnas, que permitan la comparación entre atributos y variables; por ejemplo: Marcas vs características.
Permite el relacionamiento de los atributos; por ejemplo, si se cuenta con múltiples atributos y estos son similares para todos los productos, se podrían agrupar.
En caso de contar con grupos cercanos, el análisis permitiría identificar grupos caracterizados por los atributos que se encuentren muy relacionados
Se puede decir que la técnica permite la extracción de grupos de una forma similar al análisis de componentes principales, pero en este caso para variables categóricas.
Su principal desventaja es ser una técnica netamente descriptiva por lo que no es apta para inferencias.
En el análisis de correspondencias, trazamos un punto para cada fila y un punto para cada columna de la tabla de contingencia. Estos puntos son proyecciones de las filas y columnas de la tabla de contingencia sobre un espacio euclidiano bidimensional.
El objetivo es preservar en la medida de lo posible la relación de las filas (o columnas) entre sí en un espacio bidimensional.
Si dos puntos de fila están muy juntos, los perfiles de las dos filas (a lo largo de las columnas) son similares. Del mismo modo, dos puntos de columna que están muy juntos representan columnas con perfiles similares en las filas.
Tabla de contingencia:
Una tabla de contingencia se puede definir como una representación tabular donde se visualizan las distribuciones de frecuencias de dos variables categóricas. Estas frecuencias pueden ser frecuencias absolutas o relativas.
Las sumas de las frecuencias de las columnas describen la distribución marginal de las variables \(X\) e \(Y\), y se les conoce como perfiles marginales entre variables. La suma de las filas indica los perfiles marginales de la variable \(X\), condicionado a los atributos de \(Y\).
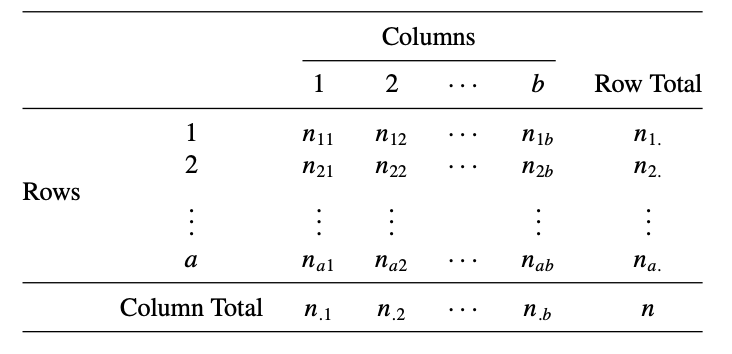
contingencia
La tabla de contingencias en frecuencias relativas también se conoce como la matriz de correspondencias.
Las frecuencias relativas no son más que el peso de cada sumatoria de frecuencias sobre el total de la fila o la columna.
Distancia entre los perfiles:
Así como en los métodos anteriores se pretendía analizar las distancias para encontrar similitudes, en este análisis se pretende el mismo objetivo; sin embargo, las distancias utilizadas para este método están determinadas por la distancia Chi-square.
Distancias \(X^2\) para las columnas:
Distancias \(X^2\) para las filas:
La distancia chi‐cuadrado cumple el principio de la equivalencia distribucional, que postula que si dos categorías tienen perfiles idénticos pueden ser sustituidas por una sola categoría que sea la suma de sus pesos, sin que con ello se modifique la distancia entre las filas o columnas.
Independencia de las tablas de correspondencias:
Para conocer si existe alguna relación entre las variables \(X\) y \(Y\) se debe realizar un contraste de hipótesis sobre la independencia de las variables, el test comúnmente se realiza bajo el estadístico de Chi-cuadrado, dado el cálculo de las distancias y con el fin de corroborar la propiedad de equivalencia. En este caso se prueban las siguientes hipótesis:
\(H_0=\) Ambas variables son independientes.
\(H_1=\) Existe una relación de dependencia.
De esta forma podemos hacer inferencia a través del \(valor-p\) a un \(\alpha\) determinado, por tanto, si:
\(Vp\leq 0.05\) se rechaza \(H_0\) y se infiere que \(X\) y \(Y\) son dependientes y en este caso conviene analizar los perfiles condicionales fila y columna, así como los residuos del modelo para estudiar qué tipo dependencia existe entre ellas.
Análisis de Correspondencias Clásico:
Una vez obtenidos los perfiles de filas y columnas, se elabora una matriz de coordenadas chi-cuadrado, calculando la relación entre la tabla de datos analizada y una tabla de datos sin relación entre variables.
En general, la idea es construir un sistema de coordenadas bidimensional asociado a las filas y columnas de la tabla de contingencia reflejando las relaciones entre ellas.
Paso 1: Obtención de los centros de gravedad e inercias
Para este método no se miden las distancias entre filas y columnas, sino que con la distancias media ponderada a su masa (proporción del conjunto).
Este perfil medio, se conoce como el centro de gravedad y la distancia media de las filas se conoce como inercia, y análogamente con las columnas, se conocerá como inercia de las columnas. Esto reflejará la matriz de varianzas y covarianzas entre las variables y sus atributos
Paso 2: Diagonalizar la matriz
Se procede a diagonalizar la matriz de varianzas y covarianzas, para obtener los valores propios que definen los ejes de proyección de las nuevas coordenadas, en este caso su obtención estará basada en la inercia y podrá representarse de forma gráfica en 2 o 3 dimensiones para tener una visión simplificada de las relaciones
En resumen, se buscará encontrar dos matrices (A,B) de coordenadas cartesianas

matrizAB
Paso 3: Interpretación
Su interpretación puede ser análoga al caso de componentes principales. Donde se está cuantificando el grado de dependía entre las variables \(X\) y \(Y\).
En este caso particular, se calculan las proporciones de inercia total explicada para cada dimensión, que ponderan la importancia de cada dimensión basado en las dependencias observadas.
La inercia acumulada permitirá conocer el número óptimo de dimensiones necesarias para explicar al máximo las dependencias.
Contribuciones Totales y Relativas:
También de forma similar al ACP o al AF se calcularán las contribuciones totales de cada variable a los ejes, de esta forma se materializan los ejes por medio del análisis de correspondencias.
Por su parte las contribuciones relativas miden la importancia de cada factor para explicar la posición en el diagrama cartesiano, representando así la distancia al origen de coordenadas de cada factor.
De las formas que en otros modelos hablamos de disimilitudes, o unicidades, aquí podemos encontrar los elementos suplementarios que son elementos de las tablas de contingencia no fueron utilizados para encontrar los ejes.
Análisis de correspondencias Múltiple:
Para esta técnica se aplican tablas de contingencia, pero ya no se comparan entre si las variables, sino que se pretende encontrar relaciones entre \(n\) filas que contienen individuos u observaciones y \(s\) variables categóricas con \(p\) categorías.
En este caso, la tabla de contingencia tiene una forma disyuntiva, es decir, se calculará la frecuencia, de forma que si el individuo i-ésimo elije una modalidad \(j\) se le asignará \(1\) y si no la elije se le asignará \(0\).
En este caso, el análisis de correspondencia se basa en la construcción de esta matriz, que se conoce como matriz de BURT, esta matriz se construye a partir de bloques, en los bloques diagonales se reportan las matrices diagonales con las frecuencias marginales de cada variable, y fuera de la diagonal están las tablas de frecuencias cruzadas de correspondientes a las combinaciones de dos variables analizadas (cada par).
En este caso, se tomará como contribución aquellas que la distribución de la inercias supera \(1/p\)

matriz_burt
El algoritmo de solución incluye igualmente la diagonalización de la matriz de distancias e inercias entre categorías, con esto también se busca la reducción de dimensionalidad a factores que representen estas inercias.
Interpretación
En este método podemos hacer interpretaciones tanto desde el relacionamiento de los individuos, igualmente, desde las modalidades de las variables diferentes, y entre las mismas variables.
Proximidades entre los individuos(semejanzas): los individuos son parecidos si elijen las mismas modalidades.
Proximidad entre modalidades de las variables diferentes: las modalidades son cercanas cuando globalmente son elegidas por los mismos individuos.
Proximidad entre modalidades en una misma variable: las modalidades de la variable son excluyentes entre si desde la construcción del instrumento, es decir, un individuo no pertenece a dos modalidades de una misma variable. Sin embargo, podría decirse que pueden ser cercanas si los individuos que la poseen presentan el mismo comportamiento en las otras variables.
Ejemplo de Matrices disyuntivas (matriz Z) y Matriz de Burt (Z.Z’)
Supongamos que cuenta con la BD de un instrumento de variables categóricas, formada por 3 variables y 10 individuos.
Individuos |
Género |
Años de experiencia |
Ingresos |
|---|---|---|---|
1 |
mujer |
5 |
medio |
2 |
mujer |
3 |
alto |
3 |
hombre |
4 |
bajo |
4 |
mujer |
1 |
bajo |
5 |
mujer |
2 |
medio |
6 |
hombre |
5 |
alto |
7 |
mujer |
2 |
medio |
8 |
hombre |
3 |
bajo |
9 |
hombre |
1 |
alto |
10 |
mujer |
4 |
medio |
La matriz disyuntiva y su transpuesta resultante sería la siguiente:
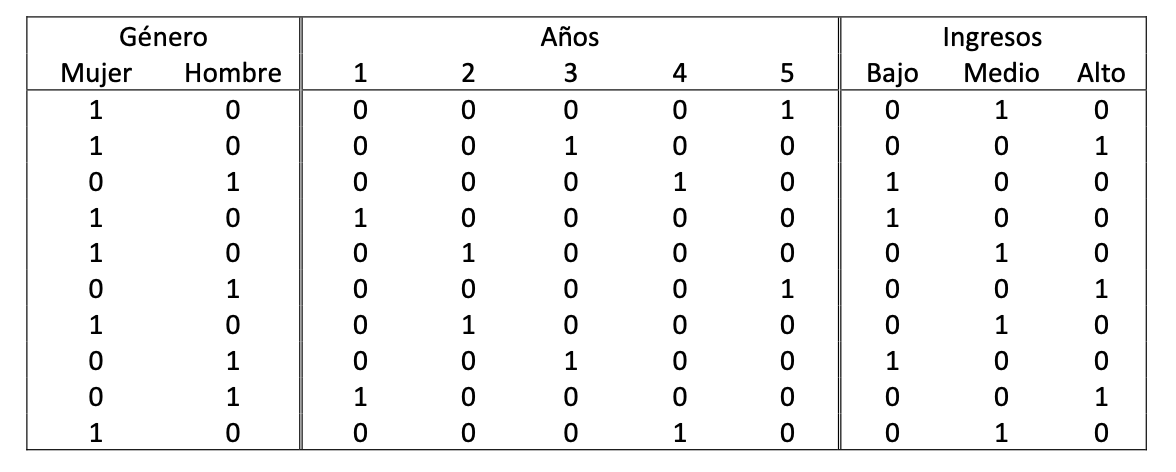
disyuntiva

BURT
Cabe aclarar que la matriz Burt sería la resultante entre las matrices \(Z\) y \(Z'\), de esta forma \(B=Z.Z'\):
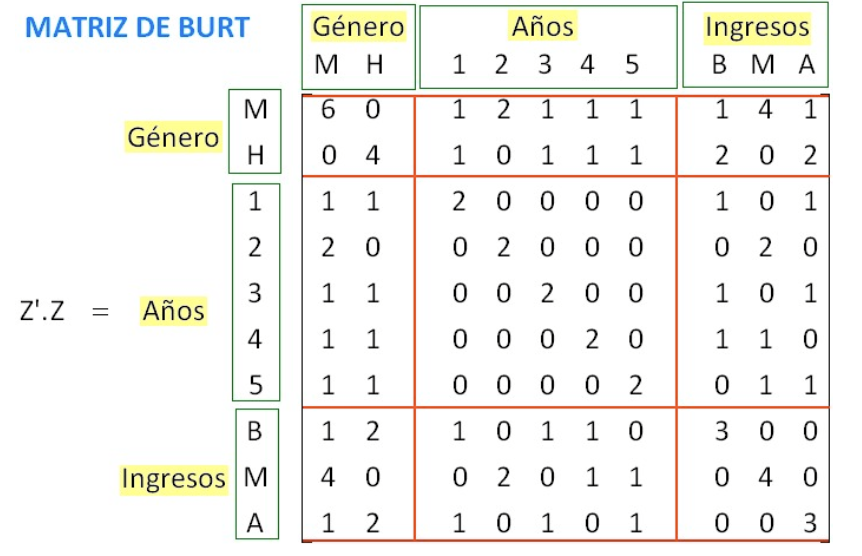
ejemplo_burt
Una vez construida la matriz, se debe realizar el test chi-cuadrado para determinar la significancia de las relaciones, tal como se realizó en el método simple, sin embargo para hacerlo, se deberá aplicar para cada par (bloque) de variables
Bibliografía: Fernández, R. S. M. (2011). Análisis de correspondencias simples y múltiples. Universidad Autónoma de Madrid: Facultad de Ciencias Económicas y Empresariales.