Análisis de correspondencias en R
Lectura de datos, el tipo de BD debe corresponder en su mayoría a variables categóricas; si se cuentan con variables continuas, estas deben reescalar a categóricas por rangos.
datos <- read.csv("creditos_otorgados_a_microempresarios-CORRESPONDENCIAS.csv", sep = ";", dec = ",", header = T)
print(head(datos))
edad sexo actividad comuna
1 62 hombre produccion 90
2 51 hombre comercio 4
3 40 mujer servicios 16
4 39 hombre produccion 90
5 35 hombre servicios 12
6 43 hombre produccion 80
str(datos)
'data.frame': 9425 obs. of 4 variables:
$ edad : int 62 51 40 39 35 43 36 46 47 45 ...
$ sexo : chr "hombre" "hombre" "mujer" "hombre" ...
$ actividad: chr "produccion" "comercio" "servicios" "produccion" ...
$ comuna : int 90 4 16 90 12 80 16 16 10 16 ...
datos[,"edad"] <- as.character(datos[,"edad"])
datos[,"comuna"] <- as.character(datos[,"comuna"])
str(datos)
'data.frame': 9425 obs. of 4 variables:
$ edad : chr "62" "51" "40" "39" ...
$ sexo : chr "hombre" "hombre" "mujer" "hombre" ...
$ actividad: chr "produccion" "comercio" "servicios" "produccion" ...
$ comuna : chr "90" "4" "16" "90" ...
Selección de las variables a analizar y creación de la tabla de contingencia:
df <- datos[,c("sexo", "actividad")]
La tabla de contingencia es la frecuencia de los datos por cada una de
las categorías, en donde se comparan entre los atributos, la función
table() de la base, puede hacer este conteo de frecuencias.
contingencias <- table(df)
print(contingencias)
actividad
sexo comercio produccion servicios
hombre 1921 496 753
mujer 3837 1348 1070
install.packages("gplots")
library(gplots)
Warning message:
"package 'gplots' was built under R version 4.1.3"
Attaching package: 'gplots'
The following object is masked from 'package:stats':
lowess
Graficamos las frecuencias de la tabla de contingencias para encontrar
visualmente donde hay mayores pesos. Para ello, se recomienda el uso de
la librería gplots con la función ballonplot().
balloonplot(t(contingencias), main ="Créditos otorgados a microempresarios",
xlab = "", ylab= "",
label = T, # Para mostrar los valores de cada celda en el gráfico.
show.margins = T) # Para mostrar la suma por filas.
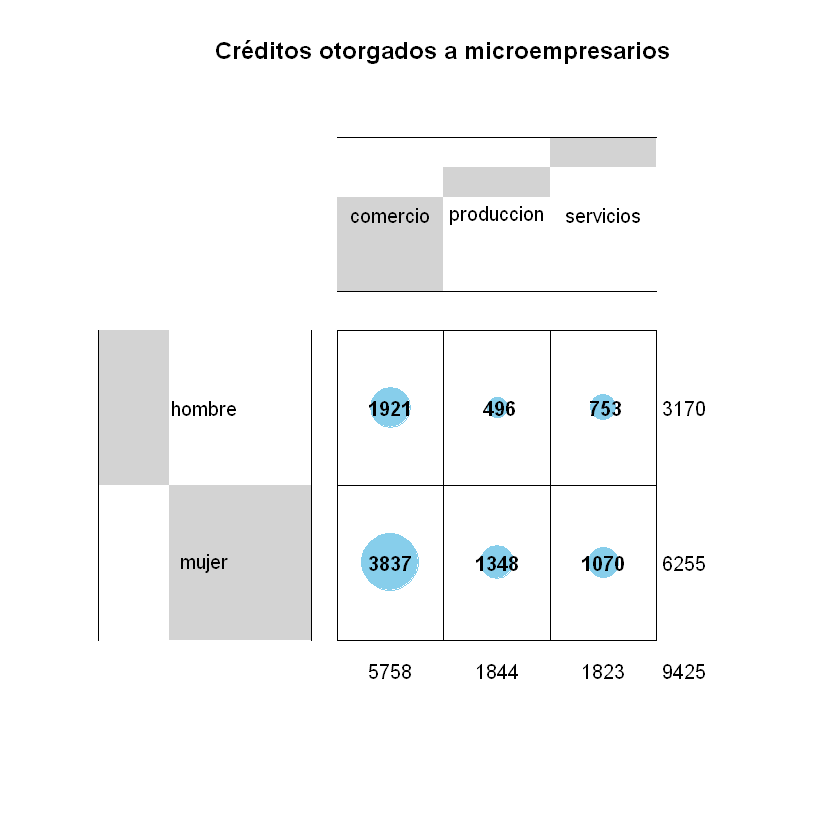
Independencia:
El análisis de la independencia debe sugerir que existen relación entre
los perfiles, por lo que al aplicar la prueba de hipótesis basado en el
estadístico chi-cuadrado, se rechaza la hipótesis nula, indicando
dependencia entre ellas. Con el paquete pander se puede realizar el
análisis.
install.packages("pander")
library(pander)
Warning message:
"package 'pander' was built under R version 4.1.3"
print(pander(chisq.test(contingencias)))
| Test statistic | df | P value | |:--------------:|:--:|:----------------:| | 85.74 | 2 | 2.411e-19 * * * | Table: Pearson's Chi-squared test: contingencias NULL
Para encontrar los perfiles o sumas marginales, simplemente se suma la matriz de contingencias y se grafica en el ballonplot.
n <- sum(contingencias)
print(n)
[1] 9425
balloonplot(t(contingencias/n), main ="Créditos otorgados a microempresarios",
xlab = "", ylab= "",
label = T,
show.margins = T)

Ahora se calculan las cargas o los pesos (centros de gravedad), primero se calculan las contribuciones por fila, y se procede a diagonalizar.
r <- rowSums(contingencias)/n
print(r)
hombre mujer
0.3363395 0.6636605
Luego se diagonaliza la matriz para encontrar las contribuciones e inercias.
Dr <- diag(r)
print(Dr)
[,1] [,2]
[1,] 0.3363395 0.0000000
[2,] 0.0000000 0.6636605
Forma diagonal de Jordan para Dr:
Extraemos los valores y vectores propios, se resuelve el sistema de ecuaciones, se calcula la inversa y se saca raiz, con esto hallamos las inercias de cada fila (atributos)
X <- eigen(Dr)
T <- X$vectors
J <- diag(x = X$values )
Tinv <- solve(T)
Jinvsqrt <- diag(x = 1/sqrt(X$values))
Drinvsqrt <- T %*% Jinvsqrt %*% Tinv
Contribución por columna:
c <- colSums(contingencias)/n
print(c)
comercio produccion servicios
0.6109284 0.1956499 0.1934218
Dc <- diag(c)
print(Dc)
[,1] [,2] [,3]
[1,] 0.6109284 0.0000000 0.0000000
[2,] 0.0000000 0.1956499 0.0000000
[3,] 0.0000000 0.0000000 0.1934218
Forma diagonal de Jordan para Dc:
Se repite l mismo procedimiento pero esta vez para las columnas.
X <- eigen(Dc)
T <- X$vectors
J <- diag(x = X$values)
Tinv <- solve(T)
Jinvsqrt <- diag(x = 1/sqrt(X$values) )
Dcinvsqrt <- T %*% Jinvsqrt %*% Tinv
P <- as.matrix(contingencias/n)
print(P)
actividad
sexo comercio produccion servicios
hombre 0.20381963 0.05262599 0.07989390
mujer 0.40710875 0.14302387 0.11352785
S <- Drinvsqrt %*% (P - r %*% t(c)) %*% Dcinvsqrt
print(S)
[,1] [,2] [,3]
[1,] -0.003661456 -0.05137440 0.05817669
[2,] 0.002606572 0.03657318 -0.04141569
print(n*sum(diag(S %*% t(S))))
[1] 85.73841
print(svd(S %*% t(S)))
$d
[1] 9.096913e-03 7.065994e-19
$u
[,1] [,2]
[1,] -0.8146536 0.5799479
[2,] 0.5799479 0.8146536
$v
[,1] [,2]
[1,] -0.8146536 0.5799479
[2,] 0.5799479 0.8146536
Contribución a la inercia por filas:
Perfiles por fila:
Cálculo de las inercias para el resto de la matriz
N_tot <- cbind(contingencias, Total = rowSums(contingencias))
N_tot <- rbind(N_tot, Total = colSums(N_tot))
print(N_tot)
comercio produccion servicios Total
hombre 1921 496 753 3170
mujer 3837 1348 1070 6255
Total 5758 1844 1823 9425
perfil_fila <- prop.table(as.matrix(N_tot[, -ncol(N_tot)]), 1)
print(perfil_fila)
comercio produccion servicios
hombre 0.6059937 0.1564669 0.2375394
mujer 0.6134293 0.2155076 0.1710631
Total 0.6109284 0.1956499 0.1934218
Perfil de los hombres:
print(prop.table(as.matrix(N_tot[, -ncol(N_tot)]), 1)[1,])
comercio produccion servicios
0.6059937 0.1564669 0.2375394
Perfil de los mujeres:
print(prop.table(as.matrix(N_tot[, -ncol(N_tot)]), 1)[2,]) # Row prof
comercio produccion servicios
0.6134293 0.2155076 0.1710631
Perfiles de columna:
print(N_tot)
comercio produccion servicios Total
hombre 1921 496 753 3170
mujer 3837 1348 1070 6255
Total 5758 1844 1823 9425
perfil_columna <- prop.table(as.matrix(N_tot[-nrow(N_tot),]),2) # Col prof
print(perfil_columna)
comercio produccion servicios Total
hombre 0.3336228 0.2689805 0.4130554 0.3363395
mujer 0.6663772 0.7310195 0.5869446 0.6636605
Cálculo de las distancias e identificación de similitudes (bajo Chi-cuadrado)
Razones de contingencia:
print(prop.table(as.matrix(N_tot[-nrow(N_tot),]),2)[,1] / prop.table(as.matrix(N_tot[-nrow(N_tot),]),2)[,ncol(contingencias)])
hombre mujer
0.807695 1.135332
Distancia Chi-cuadrado:
print(sqrt(sum((perfil_fila[1,] - perfil_fila[3,])^2 / perfil_fila[3,])))
[1] 0.1339772
Distancia entre hombre y mujer:
print(sqrt(sum( (perfil_fila[1,] - perfil_fila[2,])^2 / perfil_fila[3,])))
[1] 0.2018762
Contribución Chi-cuadrado:
Exploración de los residuales estandarizados de cada casilla y su contribución.
chisq <- chisq.test(contingencias)
print(chisq)
Pearson's Chi-squared test
data: contingencias
X-squared = 85.738, df = 2, p-value < 2.2e-16
library(corrplot)
corrplot 0.92 loaded
Contribuciones de las filas hacia las columnas. los valores en rojo reflejan menores asociaciones y los azules mayores, el tamaño indica la intensidad de la asociación. sin embargo, se observa mejor en el gráfico de proporciones de contribución.
corrplot(chisq$residuals, is.cor = FALSE, main='Residuales')
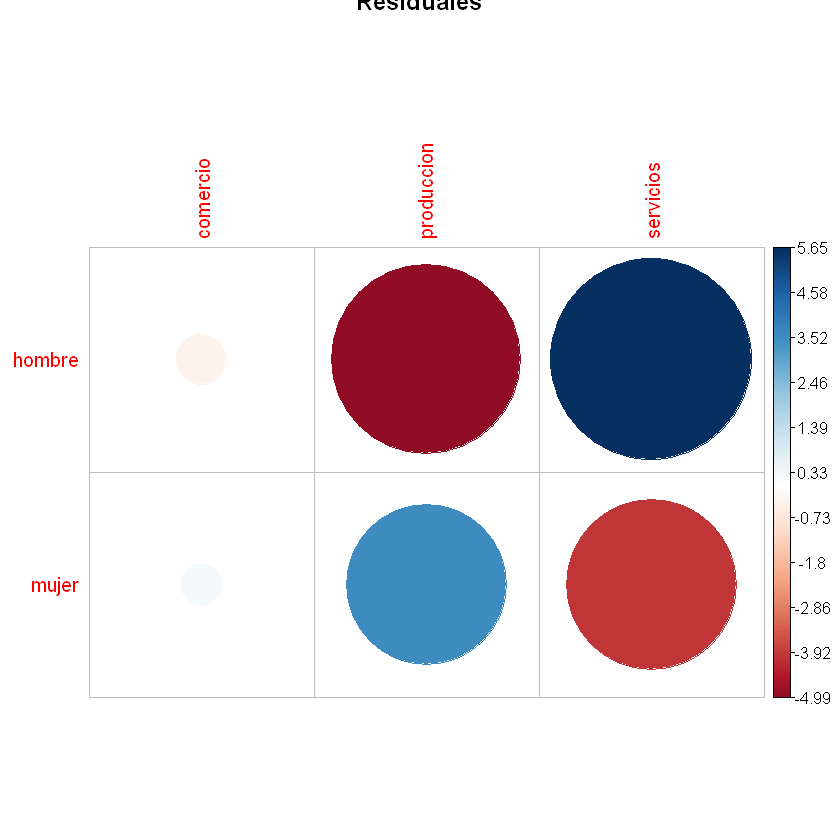
Contribución en porcentaje:
Contribución de los residuales de Pearson a la celda. Si se buscan asociaciones, se espera encontrar más cercanía entre las celdas donde la relación sea positiva y el tamaño sea el mayor.
contrib <- 100*chisq$residuals^2/chisq$statistic
corrplot(contrib, is.cor = FALSE, main='Contribución de cada celda al Chi²')
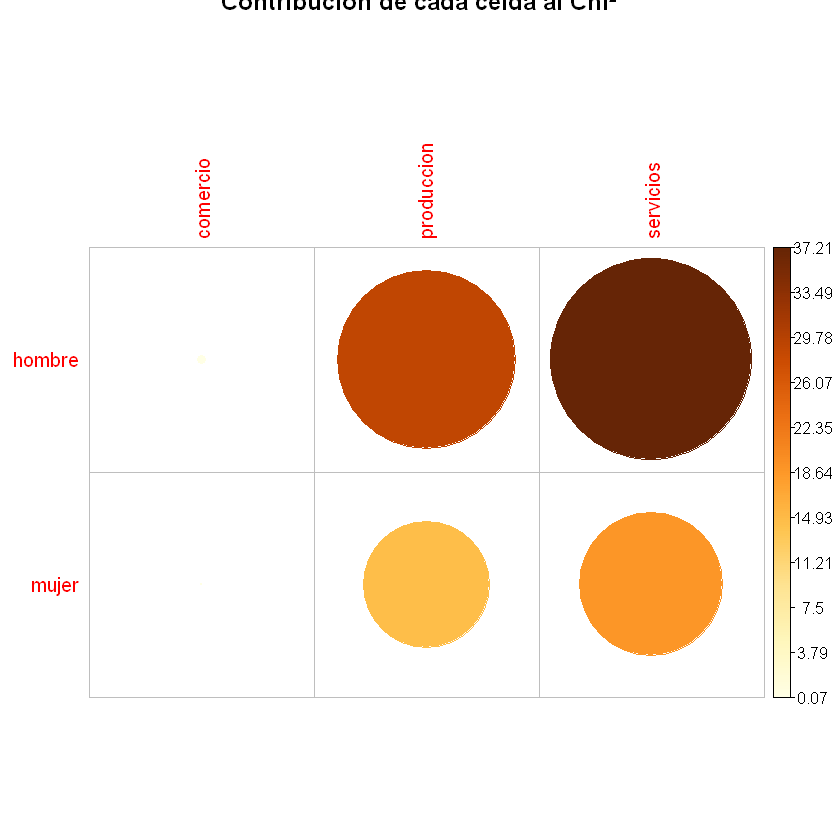
Contribución por fila:
Porcentaje de representación por contribución por modalidad.
print(rowSums(chisq$residuals^2)/n)
hombre mujer
0.006037262 0.003059652
Múltiple - MCA:
Siguiendo el mismo proceso, pero ya con múltiples variables y
modalidades, se procede con el análisis múltiple, en este caso, su
cálculo manual es más complejo por lo que se utiliza la librería
FactoExtra con la función MCA(). Para el cálculo de la matriz de
contingencias por bloques o mejor conocidas como matriz de BURT. La
librería FactoMiner también proporciona soluciones.
library(FactoMineR)
library(factoextra)
library(ca)
Warning message:
"package 'FactoMineR' was built under R version 4.1.3"
Warning message:
"package 'factoextra' was built under R version 4.1.3"
Loading required package: ggplot2
Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa
Warning message:
"package 'ca' was built under R version 4.1.3"
En el caso de hacer análisis de correspondencias múltiple, se debe especificar el argumento método, para determinar el cálculo con la matriz “BURT”, si se deja por defecto el método, utilizará la matriz de indicadoras.
res_mca <- MCA(datos,method = 'Burt')
summary(res_mca)
Call:
MCA(X = datos, method = "Burt")
Eigenvalues
Dim.1 Dim.2 Dim.3 Dim.4 Dim.5 Dim.6 Dim.7
Variance 0.098 0.085 0.080 0.077 0.076 0.076 0.075
% of var. 1.952 1.698 1.598 1.533 1.514 1.504 1.488
Cumulative % of var. 1.952 3.649 5.248 6.781 8.295 9.799 11.287
Dim.8 Dim.9 Dim.10 Dim.11 Dim.12 Dim.13 Dim.14
Variance 0.074 0.074 0.073 0.072 0.072 0.071 0.071
% of var. 1.471 1.463 1.444 1.435 1.431 1.421 1.417
Cumulative % of var. 12.758 14.221 15.665 17.100 18.531 19.951 21.368
Dim.15 Dim.16 Dim.17 Dim.18 Dim.19 Dim.20 Dim.21
Variance 0.070 0.070 0.070 0.069 0.068 0.068 0.067
% of var. 1.403 1.397 1.386 1.379 1.359 1.346 1.330
Cumulative % of var. 22.771 24.168 25.554 26.933 28.293 29.638 30.968
Dim.22 Dim.23 Dim.24 Dim.25 Dim.26 Dim.27 Dim.28
Variance 0.066 0.065 0.063 0.063 0.063 0.063 0.063
% of var. 1.312 1.299 1.244 1.244 1.244 1.244 1.244
Cumulative % of var. 32.280 33.579 34.823 36.066 37.310 38.554 39.797
Dim.29 Dim.30 Dim.31 Dim.32 Dim.33 Dim.34 Dim.35
Variance 0.063 0.063 0.063 0.063 0.063 0.063 0.063
% of var. 1.244 1.244 1.244 1.244 1.244 1.244 1.244
Cumulative % of var. 41.041 42.285 43.528 44.772 46.016 47.259 48.503
Dim.36 Dim.37 Dim.38 Dim.39 Dim.40 Dim.41 Dim.42
Variance 0.063 0.063 0.063 0.063 0.063 0.062 0.062
% of var. 1.244 1.244 1.244 1.244 1.244 1.244 1.244
Cumulative % of var. 49.747 50.990 52.234 53.478 54.721 55.965 57.208
Dim.43 Dim.44 Dim.45 Dim.46 Dim.47 Dim.48 Dim.49
Variance 0.062 0.062 0.062 0.062 0.062 0.062 0.062
% of var. 1.244 1.244 1.244 1.244 1.244 1.244 1.244
Cumulative % of var. 58.452 59.696 60.939 62.183 63.427 64.670 65.914
Dim.50 Dim.51 Dim.52 Dim.53 Dim.54 Dim.55 Dim.56
Variance 0.062 0.062 0.062 0.062 0.062 0.062 0.062
% of var. 1.244 1.244 1.244 1.244 1.244 1.244 1.244
Cumulative % of var. 67.158 68.401 69.645 70.889 72.132 73.376 74.620
Dim.57 Dim.58 Dim.59 Dim.60 Dim.61 Dim.62 Dim.63
Variance 0.062 0.059 0.059 0.058 0.057 0.056 0.056
% of var. 1.244 1.173 1.166 1.148 1.144 1.120 1.117
Cumulative % of var. 75.863 77.036 78.202 79.350 80.493 81.614 82.730
Dim.64 Dim.65 Dim.66 Dim.67 Dim.68 Dim.69 Dim.70
Variance 0.056 0.055 0.055 0.054 0.054 0.053 0.053
% of var. 1.109 1.099 1.088 1.083 1.072 1.064 1.057
Cumulative % of var. 83.839 84.938 86.027 87.109 88.181 89.245 90.303
Dim.71 Dim.72 Dim.73 Dim.74 Dim.75 Dim.76 Dim.77
Variance 0.053 0.052 0.052 0.051 0.051 0.049 0.049
% of var. 1.052 1.042 1.026 1.018 1.011 0.980 0.976
Cumulative % of var. 91.355 92.397 93.424 94.441 95.453 96.433 97.409
Dim.78 Dim.79 Dim.80
Variance 0.048 0.042 0.040
% of var. 0.957 0.845 0.789
Cumulative % of var. 98.366 99.211 100.000
Individuals (the 10 first)
Dim.1 ctr cos2 Dim.2 ctr cos2 Dim.3 ctr cos2
1 | -0.084 0.000 0.000 | -0.323 0.004 0.003 | 0.852 0.027 0.019 |
2 | 0.191 0.001 0.003 | 0.534 0.010 0.022 | 0.334 0.004 0.009 |
3 | 0.228 0.002 0.003 | -0.868 0.027 0.038 | 0.303 0.003 0.005 |
4 | 0.225 0.002 0.002 | -0.546 0.011 0.011 | 0.385 0.006 0.006 |
5 | 1.018 0.035 0.042 | -1.130 0.046 0.052 | -0.691 0.018 0.020 |
6 | -0.348 0.004 0.005 | -0.145 0.001 0.001 | 1.138 0.049 0.052 |
7 | 0.742 0.019 0.034 | 0.223 0.002 0.003 | 0.670 0.017 0.028 |
8 | 0.830 0.023 0.036 | -0.415 0.006 0.009 | 1.018 0.039 0.055 |
9 | 1.099 0.041 0.079 | 0.174 0.001 0.002 | -0.289 0.003 0.005 |
10 | -0.231 0.002 0.003 | 0.048 0.000 0.000 | 0.421 0.007 0.009 |
Categories (the 10 first)
Dim.1 ctr cos2 v.test Dim.2 ctr cos2 v.test
edad_18 | 0.538 0.180 0.003 2.584 | -0.737 0.389 0.005 -3.540 |
edad_19 | 0.348 0.502 0.008 4.345 | -0.107 0.054 0.001 -1.329 |
edad_20 | 0.384 0.610 0.010 4.790 | -0.242 0.279 0.004 -3.020 |
edad_21 | 0.380 0.784 0.012 5.442 | -0.859 4.615 0.064 -12.315 |
edad_22 | 0.440 0.977 0.016 6.073 | -0.509 1.507 0.021 -7.033 |
edad_23 | 0.226 0.292 0.005 3.323 | -0.422 1.174 0.016 -6.215 |
edad_24 | 0.364 0.733 0.012 5.265 | -0.443 1.253 0.017 -6.419 |
edad_25 | 0.311 0.649 0.010 4.966 | -0.356 0.979 0.014 -5.685 |
edad_26 | 0.168 0.196 0.003 2.726 | -0.144 0.164 0.002 -2.328 |
edad_27 | 0.391 1.018 0.016 6.218 | -0.291 0.649 0.009 -4.630 |
Dim.3 ctr cos2 v.test
edad_18 -0.390 0.116 0.001 -1.874 |
edad_19 0.126 0.080 0.001 1.570 |
edad_20 -0.500 1.265 0.016 -6.240 |
edad_21 -0.175 0.203 0.003 -2.505 |
edad_22 0.452 1.259 0.016 6.237 |
edad_23 -0.373 0.972 0.013 -5.488 |
edad_24 0.024 0.004 0.000 0.347 |
edad_25 0.215 0.378 0.005 3.430 |
edad_26 0.383 1.238 0.016 6.207 |
edad_27 0.193 0.302 0.004 3.065 |
Categorical variables (eta2)
Dim.1 Dim.2 Dim.3
edad | 0.305 0.462 0.457 |
sexo | 0.386 0.014 0.051 |
actividad | 0.326 0.329 0.146 |
comuna | 0.236 0.362 0.480 |
Extracción de los centros de gravedad o masas:
print(colSums(res_mca$var$contrib))
Dim 1 Dim 2 Dim 3 Dim 4 Dim 5
100 100 100 100 100
Análisis de los residuales de la matriz y sus contribuciones a las dimensiones, se realiza por el método de sedimentación en este caso, minimizando las distancias chi-cuadrado. Para este caso 1 dimensión bastaría, para recoger el 98% de las inercias.
res_mjca <- mjca(datos, lambda = 'Burt')
summary(res_mjca)
Principal inertias (eigenvalues):
dim value % cum% scree plot
1 0.098091 2.0 2.0 *
2 0.085315 1.7 3.6
3 0.080311 1.6 5.2
4 0.077062 1.5 6.8
5 0.076107 1.5 8.3
6 0.075565 1.5 9.8
7 0.074772 1.5 11.3
8 0.073923 1.5 12.8
9 0.073512 1.5 14.2
10 0.072593 1.4 15.7
11 0.072098 1.4 17.1
12 0.071911 1.4 18.5
13 0.071388 1.4 20.0
14 0.071205 1.4 21.4
15 0.070499 1.4 22.8
16 0.070206 1.4 24.2
17 0.069676 1.4 25.6
18 0.069300 1.4 26.9
19 0.068321 1.4 28.3
20 0.067620 1.3 29.6
21 0.066832 1.3 31.0
22 0.065913 1.3 32.3
23 0.065299 1.3 33.6
24 0.062500 1.2 34.8
25 0.062500 1.2 36.1
26 0.062500 1.2 37.3
27 0.062500 1.2 38.6
28 0.062500 1.2 39.8
29 0.062500 1.2 41.0
30 0.062500 1.2 42.3
31 0.062500 1.2 43.5
32 0.062500 1.2 44.8
33 0.062500 1.2 46.0
34 0.062500 1.2 47.3
35 0.062500 1.2 48.5
36 0.062500 1.2 49.7
37 0.062500 1.2 51.0
38 0.062500 1.2 52.2
39 0.062500 1.2 53.5
40 0.062500 1.2 54.7
41 0.062500 1.2 56.0
42 0.062500 1.2 57.2
43 0.062500 1.2 58.5
44 0.062500 1.2 59.7
45 0.062500 1.2 60.9
46 0.062500 1.2 62.2
47 0.062500 1.2 63.4
48 0.062500 1.2 64.7
49 0.062500 1.2 65.9
50 0.062500 1.2 67.2
51 0.062500 1.2 68.4
52 0.062500 1.2 69.6
53 0.062500 1.2 70.9
54 0.062500 1.2 72.1
55 0.062500 1.2 73.4
56 0.062500 1.2 74.6
57 0.062500 1.2 75.9
58 0.058926 1.2 77.0
59 0.058607 1.2 78.2
60 0.057684 1.1 79.3
61 0.057474 1.1 80.5
62 0.056309 1.1 81.6
63 0.056111 1.1 82.7
64 0.055720 1.1 83.8
65 0.055230 1.1 84.9
66 0.054697 1.1 86.0
67 0.054425 1.1 87.1
68 0.053872 1.1 88.2
69 0.053470 1.1 89.2
70 0.053134 1.1 90.3
71 0.052886 1.1 91.4
72 0.052378 1.0 92.4
73 0.051578 1.0 93.4
74 0.051149 1.0 94.4
75 0.050830 1.0 95.5
76 0.049258 1.0 96.4
77 0.049044 1.0 97.4
78 0.048114 1.0 98.4
79 0.042474 0.8 99.2
80 0.039626 0.8 100.0
-------- -----
Total: 5.025517 100.0
Columns:
name mass qlt inr k=1 cor ctr k=2 cor ctr
1 | edad:18 | 1 8 12 | -538 3 2 | 737 5 4 |
2 | edad:19 | 4 9 12 | -348 8 5 | 107 1 1 |
3 | edad:20 | 4 14 12 | -384 10 6 | 242 4 3 |
4 | edad:21 | 5 77 12 | -380 12 8 | 859 64 46 |
5 | edad:22 | 5 37 12 | -440 16 10 | 509 21 15 |
6 | edad:23 | 6 21 12 | -226 5 3 | 422 16 12 |
7 | edad:24 | 5 29 12 | -364 12 7 | 443 17 13 |
8 | edad:25 | 7 24 12 | -311 10 6 | 356 14 10 |
9 | edad:26 | 7 5 12 | -168 3 2 | 144 2 2 |
10 | edad:27 | 7 25 12 | -391 16 10 | 291 9 6 |
11 | edad:28 | 6 36 12 | -360 13 8 | 487 23 17 |
12 | edad:29 | 7 11 12 | 60 0 0 | 313 11 8 |
13 | edad:30 | 7 12 12 | -131 2 1 | 297 10 7 |
14 | edad:31 | 6 15 12 | -342 12 8 | 156 3 2 |
15 | edad:32 | 6 14 12 | 124 2 1 | 347 12 9 |
16 | edad:33 | 6 5 12 | -100 1 1 | -208 4 3 |
17 | edad:34 | 6 0 12 | 66 0 0 | 1 0 0 |
18 | edad:35 | 7 12 12 | -53 0 0 | 326 12 8 |
19 | edad:36 | 7 1 12 | -18 0 0 | -64 0 0 |
20 | edad:37 | 6 13 12 | 379 13 8 | -37 0 0 |
21 | edad:38 | 6 13 12 | 374 13 8 | 11 0 0 |
22 | edad:39 | 6 2 12 | -141 2 1 | -44 0 0 |
23 | edad:40 | 5 12 12 | 262 6 4 | 266 6 4 |
24 | edad:41 | 5 9 12 | 286 7 4 | -170 2 2 |
25 | edad:42 | 5 1 12 | 69 0 0 | -105 1 1 |
26 | edad:43 | 5 9 12 | 319 9 5 | 4 0 0 |
27 | edad:44 | 5 16 12 | 439 16 10 | -17 0 0 |
28 | edad:45 | 5 19 12 | 465 19 12 | 3 0 0 |
29 | edad:46 | 6 7 12 | 244 6 4 | -127 2 1 |
30 | edad:47 | 6 6 12 | 201 4 2 | 166 3 2 |
31 | edad:48 | 6 2 12 | 112 1 1 | 121 1 1 |
32 | edad:49 | 6 8 12 | 150 2 1 | -247 6 4 |
33 | edad:50 | 5 27 12 | 265 6 4 | -511 21 15 |
34 | edad:51 | 6 10 12 | 245 6 4 | -214 4 3 |
35 | edad:52 | 6 21 12 | 296 8 5 | -375 13 9 |
36 | edad:53 | 6 7 12 | 201 4 3 | -154 2 2 |
37 | edad:54 | 6 55 12 | 601 35 22 | -462 21 15 |
38 | edad:55 | 5 4 12 | 182 3 2 | -132 1 1 |
39 | edad:56 | 4 0 12 | 36 0 0 | 67 0 0 |
40 | edad:57 | 4 19 12 | 278 5 3 | -455 14 10 |
41 | edad:58 | 4 18 12 | -325 6 4 | -452 12 8 |
42 | edad:59 | 3 39 12 | -369 7 5 | -774 32 23 |
43 | edad:60 | 4 22 12 | -68 0 0 | -618 22 16 |
44 | edad:61 | 3 3 12 | 191 2 1 | -189 2 1 |
45 | edad:62 | 3 6 12 | 246 3 2 | -304 4 3 |
46 | edad:63 | 3 9 12 | -281 4 2 | -341 5 4 |
47 | edad:64 | 3 29 12 | -359 5 3 | -758 24 18 |
48 | edad:65 | 2 53 12 | -859 19 12 | -1124 33 24 |
49 | edad:66 | 2 28 12 | -268 2 1 | -1048 27 19 |
50 | edad:67 | 1 5 12 | -441 4 2 | -264 1 1 |
51 | edad:68 | 1 30 12 | -905 11 7 | -1165 18 13 |
52 | edad:69 | 1 2 12 | 33 0 0 | -384 2 1 |
53 | edad:70 | 0 12 12 | -1331 12 8 | -266 0 0 |
54 | edad:71 | 0 9 12 | -607 2 1 | -1001 6 5 |
55 | edad:72 | 0 2 12 | -790 1 1 | -546 1 0 |
56 | edad:73 | 0 18 12 | -1523 3 2 | -3389 15 11 |
57 | edad:74 | 0 5 12 | 1574 2 1 | -1726 3 2 |
58 | edad:75 | 0 29 12 | -4185 15 9 | -4076 14 10 |
59 | sexo:hombre | 84 482 9 | -488 465 204 | -91 16 8 |
60 | sexo:mujer | 166 482 4 | 247 465 104 | 46 16 4 |
61 | actividad:comercio | 153 278 5 | -52 16 4 | -206 261 76 |
62 | actividad:produccion | 49 321 10 | 580 319 168 | 48 2 1 |
63 | actividad:servicios | 48 505 10 | -424 168 89 | 601 337 205 |
64 | comuna:1 | 23 20 11 | -15 0 0 | 224 20 13 |
65 | comuna:10 | 21 433 12 | -665 157 94 | -879 275 189 |
66 | comuna:11 | 2 16 12 | -635 16 10 | -130 1 0 |
67 | comuna:12 | 4 24 12 | -310 7 4 | 484 17 12 |
68 | comuna:13 | 19 19 12 | 183 11 7 | 155 8 5 |
69 | comuna:14 | 1 0 12 | -25 0 0 | 74 0 0 |
70 | comuna:15 | 4 25 12 | -282 5 3 | 557 20 15 |
71 | comuna:16 | 9 21 12 | -371 20 12 | 101 1 1 |
72 | comuna:2 | 14 31 12 | -44 0 0 | 361 31 22 |
73 | comuna:3 | 14 9 12 | 161 6 4 | -105 3 2 |
74 | comuna:4 | 31 9 11 | 56 2 1 | -113 7 5 |
75 | comuna:5 | 15 3 12 | 97 2 1 | -52 1 0 |
76 | comuna:50 | 1 11 12 | 708 5 3 | -815 6 5 |
77 | comuna:6 | 13 7 12 | 154 5 3 | 77 1 1 |
78 | comuna:60 | 8 37 12 | 452 27 17 | -265 9 7 |
79 | comuna:7 | 24 3 11 | 46 1 1 | 71 2 1 |
80 | comuna:70 | 0 2 12 | -410 1 1 | 385 1 1 |
81 | comuna:8 | 14 39 12 | 401 39 24 | 34 0 0 |
82 | comuna:80 | 5 4 12 | 24 0 0 | 210 4 3 |
83 | comuna:9 | 21 2 11 | 56 1 1 | 43 1 0 |
84 | comuna:90 | 4 41 12 | -233 4 2 | 726 37 27 |
Analisis de dependencia por bloque
chisq.test(datos$edad, datos$sexo)
Warning message in chisq.test(datos$edad, datos$sexo):
"Chi-squared approximation may be incorrect"
Pearson's Chi-squared test
data: datos$edad and datos$sexo
X-squared = 161.15, df = 57, p-value = 7.023e-12
chisq.test(datos$edad, datos$actividad)
Warning message in chisq.test(datos$edad, datos$actividad):
"Chi-squared approximation may be incorrect"
Pearson's Chi-squared test
data: datos$edad and datos$actividad
X-squared = 250.56, df = 114, p-value = 2.975e-12
chisq.test(datos$edad, datos$comuna)
Warning message in chisq.test(datos$edad, datos$comuna):
"Chi-squared approximation may be incorrect"
Pearson's Chi-squared test
data: datos$edad and datos$comuna
X-squared = 1156.2, df = 1140, p-value = 0.3629
chisq.test(datos$actividad, datos$sexo)
Pearson's Chi-squared test
data: datos$actividad and datos$sexo
X-squared = 85.738, df = 2, p-value < 2.2e-16
chisq.test(datos$actividad, datos$comuna)
Warning message in chisq.test(datos$actividad, datos$comuna):
"Chi-squared approximation may be incorrect"
Pearson's Chi-squared test
data: datos$actividad and datos$comuna
X-squared = 154.47, df = 40, p-value = 2.298e-15