Práctica 5: Optimización de portafolios

De la sección anterior Obtención y Análisis de Rendimientos R, se analizaron los rendimientos de 6 acciones, las cuales se tomarán para este apartado.

Creación de la frontera eficiente

Para la optimización de portafolios y la obtención de la frontera eficiente, es necesario hacer uso de la librería fPortfolio. por tanto, después de instalarla, se debe llamar.

Para conocer mas argumentos de la librería ver aquí

library('fPortfolio')

Para poder trazar la línea del mercado de capitales y entontrar el portafolio tangente a la frontera eficiente, debe definirse o encontrarse una tasa libre de riesgo, la cual dependerá del mercado en el que se encuentre, en este caso, como las acciones son del mercado de Estados Unidos, se trabajará con la tasa de los bonos a 10 años de este país. Esta tasa normalmente se entiende como una nominal anual, por lo que se debe encontar la correspondiente para la periodicidad en la que se tenga el portarfolio, en este caso, diaria.

rf=0.000029

Se deben confingurar los argumentos para que la función fPortfolio optimice, es decir, cargar las especificaciones portfolioSpec()del programa optimizador en un objeto llamado espcartera. Generalmente, se configura la tasa libre de riesgo con la función 'setRiskFreeRate<-'(), el número de puntos o portafolios que se desean mostrar en la frontera eficiente con la función 'setNFrontierPoints<-' y la restricción de no negatividad con la función constraints="longOnly".

Los resultados del modelo mostraran los parámetros con los que se configuró, por ejemplo; muestra en Type: MVque el tipo de modelo es el de Markowitz de mínima variaza. El programa optimizador Optimize:minRisk, es el que en su función objetivo minimiza el riesgo, utilizando como estimador la matriz de covarianzas Estimator:covEstimator.

espcartera=portfolioSpec()
  `setRiskFreeRate<-`(espcartera, 0.000029)
  `setNFrontierPoints<-`(espcartera, 20)
  constraints="longOnly"

Model List:
 Type:                      MV
 Optimize:                  minRisk
 Estimator:                 covEstimator
 Params:                    alpha = 0.05

Portfolio List:
 Target Weights:            NULL
 Target Return:             NULL
 Target Risk:               NULL
 Risk-Free Rate:            2.9e-05
 Number of Frontier Points: 50

Optim List:
 Solver:                    solveRquadprog
 Objective:                 portfolioObjective portfolioReturn portfolioRisk
 Options:                   meq = 2
 Trace:                     FALSE

Model List:
 Type:                      MV
 Optimize:                  minRisk
 Estimator:                 covEstimator
 Params:                    alpha = 0.05

Portfolio List:
 Target Weights:            NULL
 Target Return:             NULL
 Target Risk:               NULL
 Risk-Free Rate:            0
 Number of Frontier Points: 20

Optim List:
 Solver:                    solveRquadprog
 Objective:                 portfolioObjective portfolioReturn portfolioRisk
 Options:                   meq = 2
 Trace:                     FALSE

Luego, se crea un objeto Frontera de clase fPortfolio que creará la frontera sobre los datos obtenidos de los rendimientos, esto se realiza con la función portfolioFrontier(). El objeto que configura la optimización del portafolio espcartera debe ser ajustado a los datos de los rendimientos de las acciones con las que se esté trabajando en el argumento spec =, en este caso, serán los rendimientos analizados en Obtención y Análisis de Rendimientos R. Los rendimientos tendrán que ser una serie de tiempo por lo que se utiliza la función as.timeSeries() sobre los rendimientos Rdtos[-1,]. se incluye dentro de la función el portafolio de mínima varianza con el argumento include.mvl = TRUE y el título del modelo es title = "Cartera".

Esto producirá una serie de posibles portafolios que cumplen con la carcteristica de maximizar el rendimiento dados ciertos niveles de riesgo.

Frontera= portfolioFrontier(as.timeSeries(Rdtos[-1,]), spec = espcartera, include.mvl = TRUE, title = "Cartera")
print(Frontera)

Title:
 MV Portfolio Frontier
 Estimator:         covEstimator
 Solver:            solveRquadprog
 Optimize:          minRisk
 Constraints:       LongOnly
 Portfolio Points:  5 of 50

Portfolio Weights:
   WMT.Adjusted PG.Adjusted NFLX.Adjusted KO.Adjusted JNJ.Adjusted
1        0.0000      0.0000        0.0000      1.0000       0.0000
13       0.0733      0.0000        0.0307      0.5271       0.3689
25       0.3101      0.0000        0.0849      0.2994       0.3057
37       0.4467      0.1130        0.1278      0.0915       0.2210
50       0.0000      0.0000        1.0000      0.0000       0.0000

Covariance Risk Budgets:
   WMT.Adjusted PG.Adjusted NFLX.Adjusted KO.Adjusted JNJ.Adjusted
1        0.0000      0.0000        0.0000      1.0000       0.0000
13       0.0469      0.0000        0.0182      0.5967       0.3382
25       0.2869      0.0000        0.0772      0.3253       0.3106
37       0.4611      0.1181        0.1339      0.0793       0.2076
50       0.0000      0.0000        1.0000      0.0000       0.0000

Target Returns and Risks:
     mean    Cov   CVaR    VaR
1  0.0000 0.0186 0.0520 0.0266
13 0.0002 0.0153 0.0416 0.0218
25 0.0005 0.0139 0.0343 0.0192
37 0.0007 0.0140 0.0327 0.0168
50 0.0009 0.0248 0.0583 0.0376

Description:
 Sun Aug 09 18:47:44 2020 by user: Natalia

Gráfico de la frontera eficiente

La función que permite crear el gráfico de la frontera es frontierPlot(), la cual se aplica sobre el objeto clase fPortfolio creado anteriormente, donde sus argumentos son: * frontier="both" para que contruya tanto la parte superior, como la inferior de la frontera. * col = c("black", "black") y cex=2 para el color y el tamano de los puntos que componen la frontera.

Para visualizar la nube de puntos verdes que conforman multiples parejas de riesgo y rendimiento, pero que nos on los óptimos, se utiliza la función monteCarloPoints() sobre el objeto Frontera, con los mismos argumentos de las funciones para gráficos (colores col= c("green", "green"), tamaño cex=0.5, y tipo de gráfico pch = 19), además el argumento mcSteps = 500 indicará la cantidad puntos que desea ver, este argumento se puede cambiar por cualquier número.
La línea del mercado de capitales se traza con la función tangencyLines() sobre el objeto Frontera.
Identificar el portafolio de mínima varianza (punto azul) se logra con la función minvariancePoints(), sobre el objeto Frontera y se determina color tipo de gráfico y tamaño.
Por último para visualizar el portafolio tangente, se utiliza la función tangencyPoints() sobre Frontera y con los mismos atributos anteriores.

#dev.off() opcional si se desa borrar la ventana de gráficos
frontierPlot(Frontera, frontier = "both", col = c("black", "black"), cex=2)
monteCarloPoints(Frontera,col= c("green", "green"), mcSteps = 500, cex=0.5, pch = 19)
tangencyLines(Frontera)
minvariancePoints(Frontera, col="blue", pch=19, cex=2)
tangencyPoints(Frontera, col="red", cex= 2, pch=19)

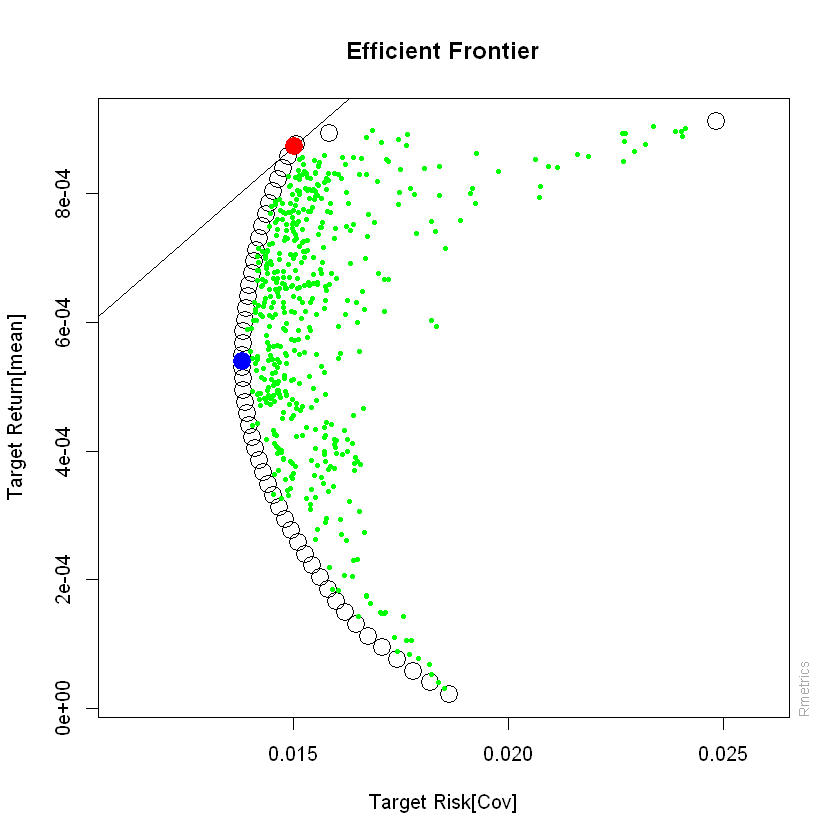
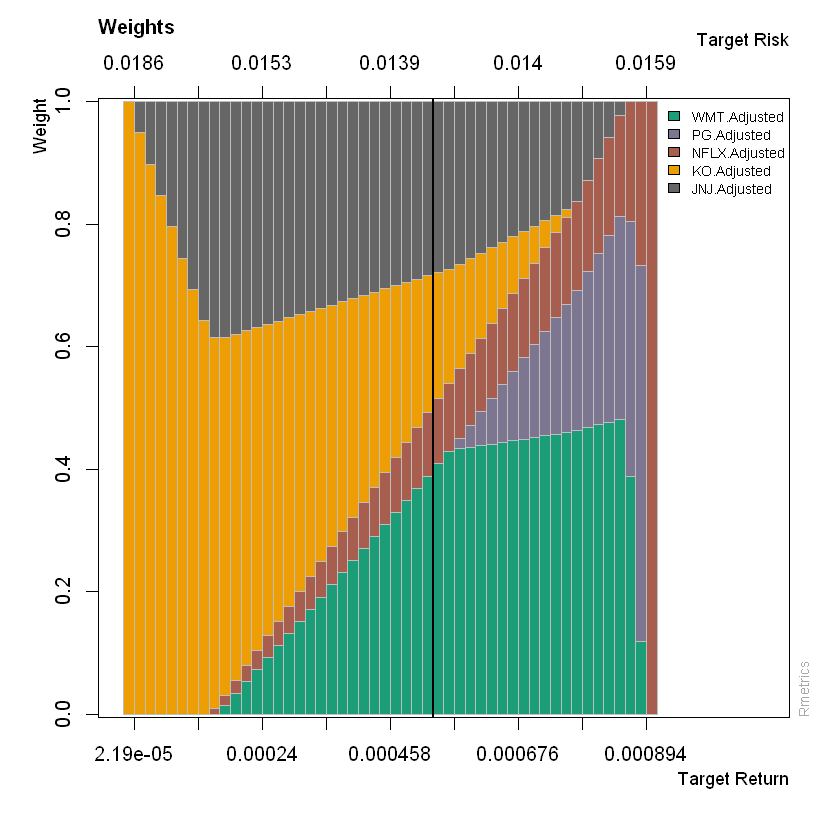
Gráfico de los pesos para los portafolios

El gráfico de pesos de los portafolios, permite visualizar las acciones que aportan a los diferentes niveles de riesgo y rendimiento, cada color representa una acción, el tamaño vertical de las barras indica el peso que debe darse a cada una, para asumir el objetivo de riesgo (absisa superior) y el objetvo de rendimiento (absisa inferior); y debe leerse en cada una de las barras; por ejemplo, la primera barra de izquierda a derecha indica que para tener un rendimiento de -0.00146 y un riesgo de 0.0243, se debe invertir un 0.5% aprox. en BABA y un 99.5% en WBA. la línea negra, indica la barra de proporciones que tiene el portafolio de mínima varianza, para el cual habría que invertir un 25% aprox en BABA un 70% en WMT, un pequeño 1% aprox en WBA y un 4% aprox. en TSLA y nada en PEP no AAPL.

Para obtener este gráfico, se utliza la función weightsPlot() sobre el objeto Frontera, con los colores definos por la paleta col= qualiPalette(ncol(Rdtos), "Dark2")

col= qualiPalette(ncol(Rdtos), "Dark2")
weightsPlot(Frontera, col=col)