Práctica 4: Obtención y Análisis de Rendimientos R
Preparación de librerías
Antes de comenzar, se deben tener instaladas las siguientes librerías para que el código funcione correctamente:
Librería
quantmodLibrería
fBasicsLibrería
fPortfolio
install.packages('quantmod')
install.packages('fBasics')
install.packages('fPortfolio')
Siempre que se vaya utilizar una librería debe ser llamada por medio del comando library, en este caso para obtener los datos de los precios de acciones de Yahoo Finance, se llamará a la librería Quantmod
library('quantmod')
Ya con la librería cargada en R, se procede con la obtención de los precios de las acciones con la función getsymbols:
Los símbolos de los nombres de las acciones, deben ser extraídos de la página Yahoo Finance
Se debe ingresar a la función como una lista de elementos entre comillas y separados por comas (,) dentro de un vector, por ello
c('simbolos')Se cambia las fechas según lo deseado, desde el inicio
from=y la fecha en formato “AAAA-MM-DD”. Igualmente, con la fecha finalto=. en este caso particular la función,Sys.Date(), obtiene la fecha de su sistema.
getSymbols.yahoo(c('BABA','AAPL','WMT', 'WBA', 'TSLA','PEP'),env=globalenv(), from = "2019-02-12",to = Sys.Date())
pausing 1 second between requests for more than 5 symbols
pausing 1 second between requests for more than 5 symbols
- 'BABA'
- 'AAPL'
- 'WMT'
- 'WBA'
- 'TSLA'
- 'PEP'
Una vez obtenidos los datos de cada una de las acciones que se escogen,
se procede a crear un objeto de formato DataFrame DF (similar a una
matriz) llamado cartera, que incluya los precios ajustados de cada
acción, con la función merge.
Para que los nombres de la cartera queden con un mejor formato, se
procede a renombrar las columnas del objeto cartera con la función
names() e ingresando el vector con la lista de nombres
c(" nombre", "nombre").
Por último, se extraen las fechas de los precios de las acciones, para crear un objeto con ellas que mas adelante permita graficar.
cartera= merge(BABA$BABA.Adjusted, AAPL$AAPL.Adjusted, WMT$WMT.Adjusted, WBA$WBA.Adjusted,TSLA$TSLA.Adjusted, PEP$PEP.Adjusted)# el simbolo $ extrae una columna de una matriz
names(cartera)<-c("BABA", "AAPL", "WMT", "WBA", "TSLA", "PEP") #vector de nombres digitados
fechas=index(cartera)
Con el fin de crear una paleta, que ayude a realizar gráficos de
distintos colores, se usa la función qualiPalette() perteneciente a la
libreria fBasics. El parámetro n=ncol(cartera) crea tantos colores
como acciones se tengan en el objeto cartera, y el argumento
name = c("Dark2") escoge la paleta de colores a utilizar. Para ver
mas colores disponibles visite la librería colorPalette Ver
aquí
library('fBasics')
colores= qualiPalette(n=ncol(cartera), name = c("Dark2"))
Creación de la matriz de rendimientos y gráfica de Rdtos
Como ya se creó el objeto cartera como DF, se pueden utilizar las
funciones diff() y log(), directamente sobre cartera y de
esta forma, obtener los rendimientos logarítmicos sobre los precios
ajustados.
Cuando se obtienen los rendimientos, siempre hay un dato menos, dentro
de la matriz, por lo que se redefine el objeto Rdtos usando
Rdtos=Rdtos[-1,]
Rdtos=diff(log(cartera))
Rdtos=Rdtos[-1,]
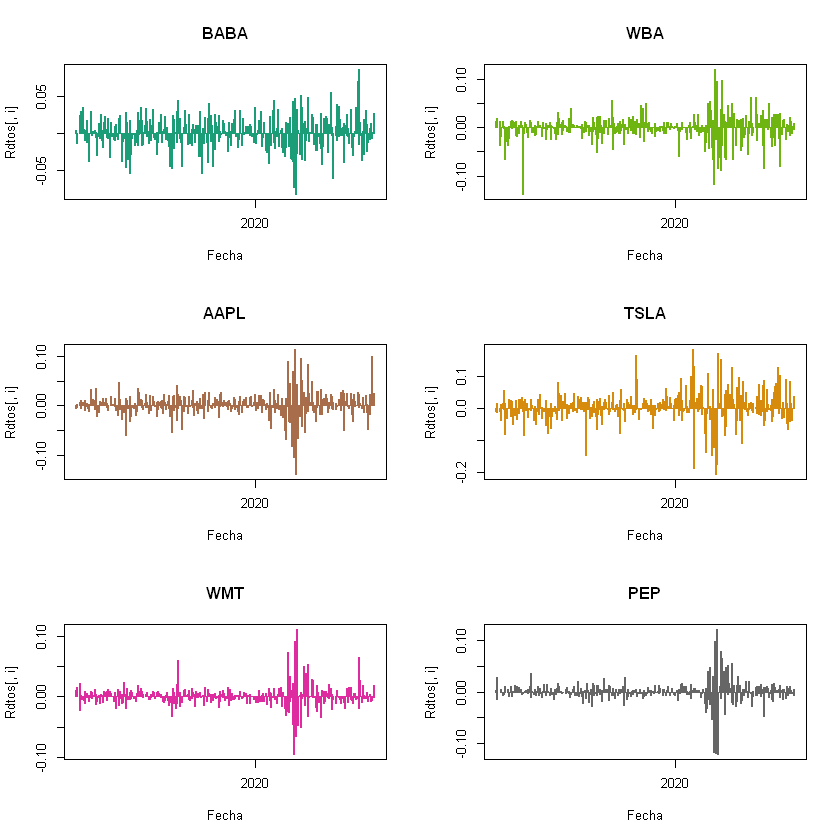
Preparación de la ventana de gráficos. (imagen 1)
Con el fin de crear una ventana, que coloque los rendimientos en una
matríz gráfica de 6x2, se crean el objeto
tamano=c(seq(ncol(cartera))), crea una secuencia de 1 hasta el
número total de acciones con el que cuenta cartera, es decir, si se
cuentan con 10 acciones en cartera, la secuencia será de 1 hasta 10.
de esta forma, la ventana gráfica que se crea con las funciones
matrix (filas, columnas), layout(matrix), y
layout.show()será de 10x2.
Gráficos de rendimientos (imagen 2)
Para el gráfico de los rendimientos se hace uso de un ciclo for,
para que recorra el objeto cartera y grafique las acciones que se
encuentran en cada una de las columnas. Así lo hará dentro de la ventana
gráfica como se muestra en la segunda imagen. la función plot(),
permite realizar las gráficas de tipo X contra Y, que en este caso sería
el objeto fechascreado anteriormente, contra la matríz de
rendimientos en la columna i Rdtos[,i] dentro de los argumentos
principales se encuentran: * main=, que corresponde al título, para
este caso particular tomará los nombres que tiene el objeto cartera
en la posicón i, es decir, el nombre que se le asignó a cada columna
anteriormente. * t= es el tipo de gáfico a usar, en este caso es
"h", pero puede cambiarse, dependiendo del gusto. * col=
pertenece al argumento color del grafico, que se usarán en este caso los
colores definidos anteriormente, por la paleta almacenada en el objeto
colores. * xlab= es el título del eje x. Para conocer mas
argumentos de la función plot() visite la doumentación Ver
aquí
#dev.off()
tamano=c(seq(ncol(cartera)))
matriz=matrix(tamano, ncol=2)
C=layout(matriz)
for(i in 1:ncol(cartera)){
plot(fechas[-1],Rdtos[,i],t="h",main = names(cartera[,i]), col=colores[i],lwd=2, xlab="Fecha")
}
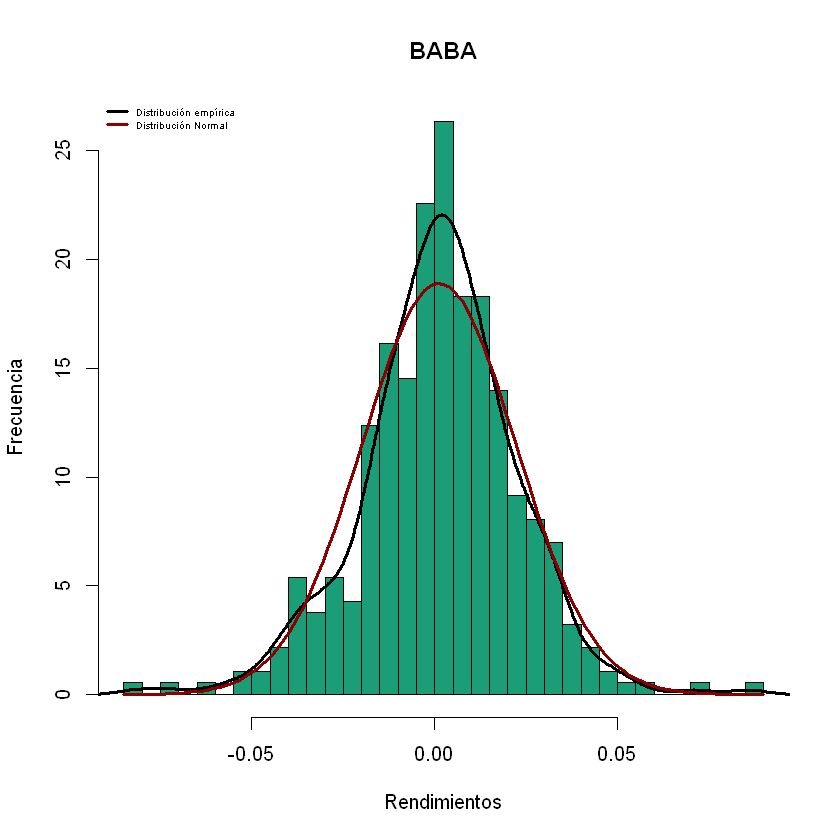
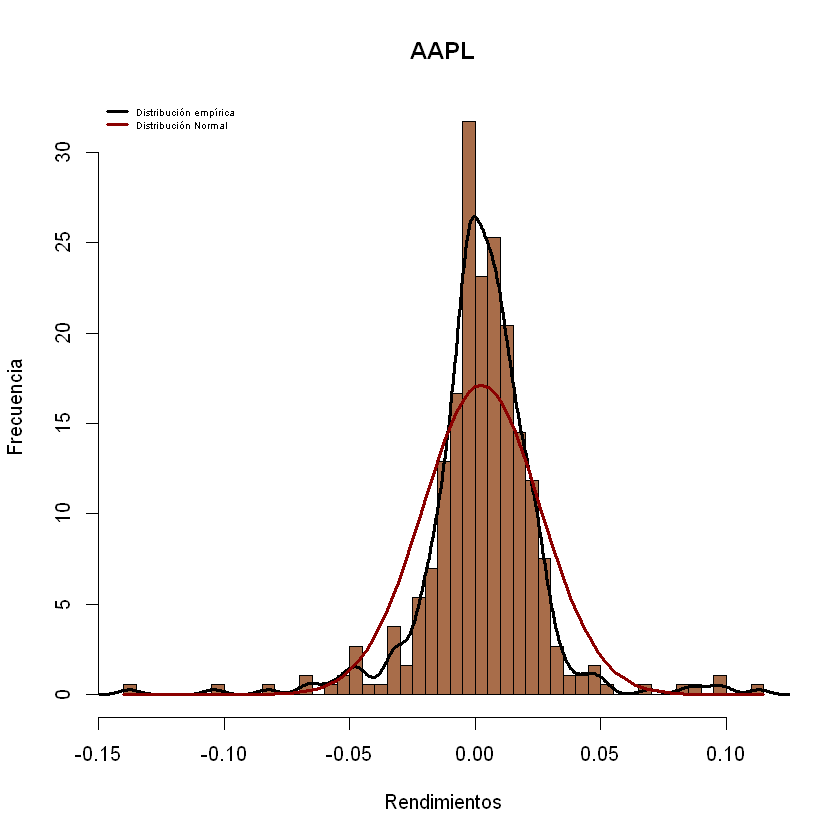
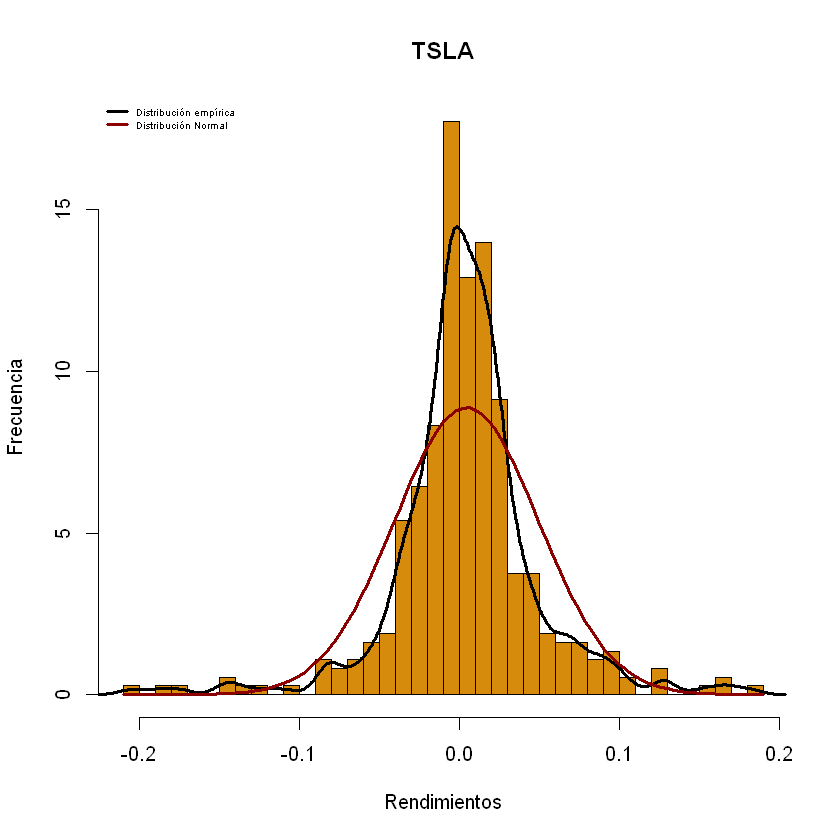
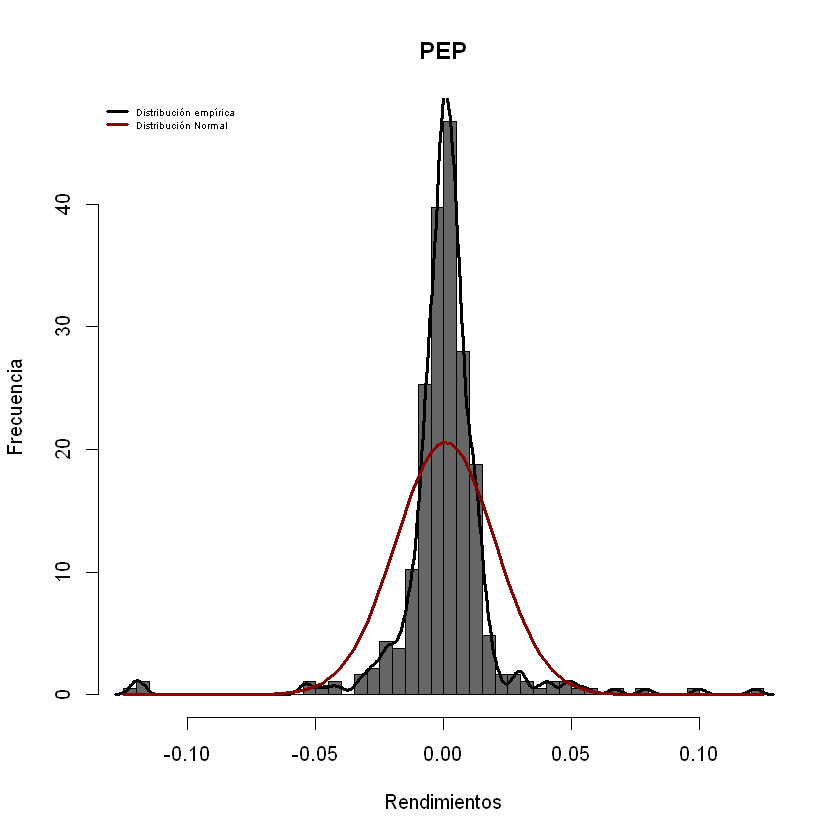
Histograma de los rendimientos
Al igual que con el gráfico anterior, puede crearse la ventana de
preparación de gráficos.
dev.off() win.graph(15,13) tamano=c(seq(ncol(cartera))) matriz=matrix(tamano, ncol=2) C=layout(matriz) layout.show(C)
Igualmente, para la creación de cada uno de los histogramas, dada la
cantidad de acciones , se realizan por medio de un ciclo for, esta
vez se hace uso de la función hist(), para los rendimientos en la
posición i Rdtos[,i] con 40 intervalos o barras breaks=40, los
demás argumentos son iguales a los de la función plot(). *
Adicionalmente, al gráfico de histograma se le ajustan las gráficas de
densidad distribución empírica de los datos (línea negra) con las
funciones lines() density(), el argumento lwd= determina el
grosor de la línea. * También, se le ajusta la curva de distribución
normal teórica (línea roja) haciendo uso de la función
curve=(dnorm(x,...))el resto de argumentos son similares a la
función plot()
for (i in 1:ncol(cartera)){
hist(Rdtos[,i],breaks = 40,col = colores[i],xlab = "Rendimientos",ylab = "Frecuencia",main = names(cartera[,i]),freq =F)
lines(density(Rdtos[,i]),lwd=3)
curve(dnorm(x,mean =mean(Rdtos[,i]),sd=sd(Rdtos[,i])),add=T,col="darkred",lwd=3)
legend(x="topleft",cex = 0.5,c("Distribución empírica","Distribución Normal"),col=c("Black","darkred"),lwd=c(3,3),bty="n")
}


Estadíticas Básicas
Las diversas estadísticas básicas que sirven para el análisis de los
redimientos, pueden ser obtenidas con las funciones: 1.
sumary()estadíticas descriptivas como el mínimo, el primer
cuantil, mediana, media, tercer cuantil y el maximo de cada una de los
rendimientos individuales de las acciones. 2. apply(Rdtos,2,mean)
aplica la función mean()a la matríz de rendimientos por columnas
(2), para encontrar el vector de los rendimientos promedios. 3.
apply(Rdtos,2,mean)aplica la función sd()a la matríz de
rendimientos por columnas (2), para encontrar el vector de las
volatilidades. 4. cor(Rdtos) obtiene la matriz de correlaciones de
los rendimientos
# 1. estadisticas básicas
print(summary(Rdtos))
Index BABA AAPL
Min. :2019-02-13 Min. :-0.081311 Min. :-0.137708
1st Qu.:2019-06-26 1st Qu.:-0.011150 1st Qu.:-0.006171
Median :2019-11-06 Median : 0.001809 Median : 0.002785
Mean :2019-11-08 Mean : 0.001185 Mean : 0.002576
3rd Qu.:2020-03-23 3rd Qu.: 0.013781 3rd Qu.: 0.013224
Max. :2020-08-04 Max. : 0.085728 Max. : 0.113157
WMT WBA TSLA
Min. :-0.0950917 Min. :-0.137025 Min. :-0.205522
1st Qu.:-0.0049237 1st Qu.:-0.011170 1st Qu.:-0.013158
Median : 0.0005883 Median : 0.001138 Median : 0.002658
Mean : 0.0008993 Mean :-0.001365 Mean : 0.004199
3rd Qu.: 0.0063656 3rd Qu.: 0.010254 3rd Qu.: 0.022765
Max. : 0.1107227 Max. : 0.118704 Max. : 0.181445
PEP
Min. :-0.1213581
1st Qu.:-0.0051897
Median : 0.0007485
Mean : 0.0006257
3rd Qu.: 0.0060834
Max. : 0.1216565
#2. media
media_rdto=apply(Rdtos,2,mean)
print(media_rdto)
BABA AAPL WMT WBA TSLA
0.0011852858 0.0025763763 0.0008992570 -0.0013646536 0.0041992525
PEP
0.0006256733
# 3. volatilidad
volatilidades=apply(Rdtos,2,sd)
print(volatilidades)
BABA AAPL WMT WBA TSLA PEP
0.02111389 0.02330573 0.01615573 0.02572770 0.04492571 0.01935819
#4. matriz de correlaciones
correlacion= cor(Rdtos)
print(correlacion)
BABA AAPL WMT WBA TSLA PEP
BABA 1.0000000 0.6264698 0.2953416 0.3502143 0.4140950 0.3668147
AAPL 0.6264698 1.0000000 0.5030225 0.4846941 0.4505610 0.6683344
WMT 0.2953416 0.5030225 1.0000000 0.4545915 0.1472673 0.6808543
WBA 0.3502143 0.4846941 0.4545915 1.0000000 0.2048999 0.4660967
TSLA 0.4140950 0.4505610 0.1472673 0.2048999 1.0000000 0.2784757
PEP 0.3668147 0.6683344 0.6808543 0.4660967 0.2784757 1.0000000
Matríz de varianzas y covarianzas
Para obtener la matriz de varianzas y covarianzas se hace uso de la
función cov(Rdtos).
covarianza= cov(Rdtos)
print(covarianza)
BABA AAPL WMT WBA TSLA
BABA 0.0004457962 0.0003082699 0.0001007441 0.0001902405 0.0003927925
AAPL 0.0003082699 0.0005431572 0.0001893987 0.0002906240 0.0004717493
WMT 0.0001007441 0.0001893987 0.0002610077 0.0001889509 0.0001068878
WBA 0.0001902405 0.0002906240 0.0001889509 0.0006619144 0.0002368305
TSLA 0.0003927925 0.0004717493 0.0001068878 0.0002368305 0.0020183194
PEP 0.0001499270 0.0003015237 0.0002129343 0.0002321356 0.0002421849
PEP
BABA 0.0001499270
AAPL 0.0003015237
WMT 0.0002129343
WBA 0.0002321356
TSLA 0.0002421849
PEP 0.0003747396
Ejercicio práctico:
Haciendo uso del comando getSymbols.yahoo de la librería
quantmod, extraiga los datos de los precios de 4 acciones que se
encuentren en Yahoo.finance,
procure que las acciones tengan una media de rendimientos contínuos
positiva. Con estas acciones, aplique el código visto anteriormente, y
concluya sobre lo siguiente:
Indique cuales son los cuantiles 1, 2 y 3 para los rendimientos de las acciones. Para todos los casos concluya lo que significa para un inversionista cada uno de estos percentiles.
Saque la media y la volatilidad de los rendimientos e indique que significan.
Reporte el coeficiente de correlación de las acciones y concluya lo que significa.