Practica 8: Crear Portafolio de Renta Fija y Variable para el mercado Colombiano
Lectura de datos en R desde un archivo .csv (excel)
Debido a que R no hace la búsqueda de activos para las páginas que reportan los activos pertenecientes al mercado colombiano (Como "Investing o la Bolsa de Valores de Colombia), para poder ingresar los datos, se debe crear y limpiar una base de datos en excel que se guarda en formato Excel.csv. Este procedimiento se describe en los vídeos Bases de datos con Investing.
Luego de contar con la BD depurada como se muestran en los vídeos. Se
procecede a utilizar el código para leer archivos de excel en
read.csv(), con la función file.choose() abrirá un explorador de
carpetas que permitirá buscar la ubicación donde se guradó el archivo de
la base de datos. los argumentos sep = ";", dec = ",", header = T
indicaran las características con las que leerá el documento.
datos = read.csv(file.choose(), sep = ";", dec = ",", header = T)
head(datos)
| Fecha | ECO | PFVAVAL | ISA | NUTRESA | Bono.a.10.años | |
|---|---|---|---|---|---|---|
| <fct> | <int> | <int> | <int> | <int> | <dbl> | |
| 1 | 26/03/2018 | 2775 | 1165 | 13080 | 25720 | 6.44 |
| 2 | 27/03/2018 | 2645 | 1155 | 13080 | 25700 | 6.36 |
| 3 | 28/03/2018 | 2615 | 1165 | 13320 | 25980 | 6.36 |
| 4 | 2/04/2018 | 2690 | 1165 | 13420 | 25920 | 6.36 |
| 5 | 3/04/2018 | 2730 | 1175 | 13660 | 25920 | 6.49 |
| 6 | 4/04/2018 | 2740 | 1190 | 13560 | 25840 | 6.52 |
Una vez leídos los datos, como en este caso se creará un portafolio con dos tipos de activos: Renta Fija y Renta Variable, se deberá separar en dos conjuntos de datos, el primero incluye los activos de renta variable (En mi caso las 4 primeras acciones), el segundo conjunto, incluye el activo de renta fija (Bono a 10 años). Este procedimiento de separar los activos se debe a que las acciones se negocian con precios por tanto, su rendimiento es la diferencia logarítmica, mientras que los activos de renta fija se negocian con tasas, por lo que, el rendimiento es la diferencia simple.
En este caso, en el cobjeto cartera_acciones= se toman las columnas
2 a la 5, donde se encuentran los precios de las acciones de éxito,
Bancolombia y Argos. En el objeto Bono= se toma solo la columna 6
que tiene los datos de las tasas del bono a 10 años.
#separar acciones del activo de renta fija
cartera_acciones= datos[,2:5]#cambiar estos numeros por las correspondientes columnas que contengan las acciones.
cartera_acciones=ts(cartera_acciones)
#Activo renta fija
Bono= datos[,6]# cambiar por la columna que contenga el bono.
Creación Matríz de Rendimientos para Diferentes Tipos de Activos
Como se indica anteriormente, se calculan dos conjuntos de rendimientos.
El primero, corresponde al rendimiento de las acciones
Rdto_acciones=, contenidas en el objeto cartera_acciones y
calculado como la diferencia logarítmica de los precios de cierre de las
acciones diff(log(cartera_acciones)). El segundo, es el rendimiento
para las tasas del bono Rdto_bono=, contenidas en el objeto
Bono, y calculado como la primera direncia de los datos
diff(Bono)
#Rendimientos para las acciones
Rdto_acciones=diff(log(cartera_acciones))
# Rendimientos para el Bono
Rdto_bono=diff(Bono)
Una vez se tengan creados los rendimientos para ambos tipos de activos,
deben unirse las bases de datos en una sola con el comando cbind,
luego se editan los nombres de las columnas para dar un mejor formato,
tal como se muestra en la siguiente tabla:
#se unen todos los rendiemientos
Rdtos=cbind(Rdto_acciones,Rdto_bono)
nombres=c(colnames(Rdto_acciones),"Bono") #editando el nombre de las columnas
colnames(Rdtos)=nombres
head(Rdtos)
| ECO | PFVAVAL | ISA | NUTRESA | Bono |
|---|---|---|---|---|
| -0.047979682 | -0.008620743 | 0.000000000 | -0.0007779075 | -0.08 |
| -0.011406968 | 0.008620743 | 0.018182319 | 0.0108360193 | 0.00 |
| 0.028277096 | 0.000000000 | 0.007479466 | -0.0023121398 | 0.00 |
| 0.014760416 | 0.008547061 | 0.017725723 | 0.0000000000 | 0.13 |
| 0.003656311 | 0.012685160 | -0.007347572 | -0.0030911926 | 0.03 |
| 0.000000000 | 0.020790770 | 0.023324673 | 0.0153612852 | 0.02 |
Análisis de los Rendimientos
Tal como se mostró en en el apartado para Obtención y Análisis de Rendimientos R, se realizan gráficos de los rendimientos de los activos. Para recordar el uso del código Remitirse aquí
#graficar los rendimientos en layout
library('fBasics')
colores= qualiPalette(n=ncol(Rdtos), name = c("Dark2"))
for(i in 1:ncol(Rdtos)){
plot(Rdtos[,i],type="h",main = nombres[i], col=colores[i],lwd=2, xlab="Fecha")
}
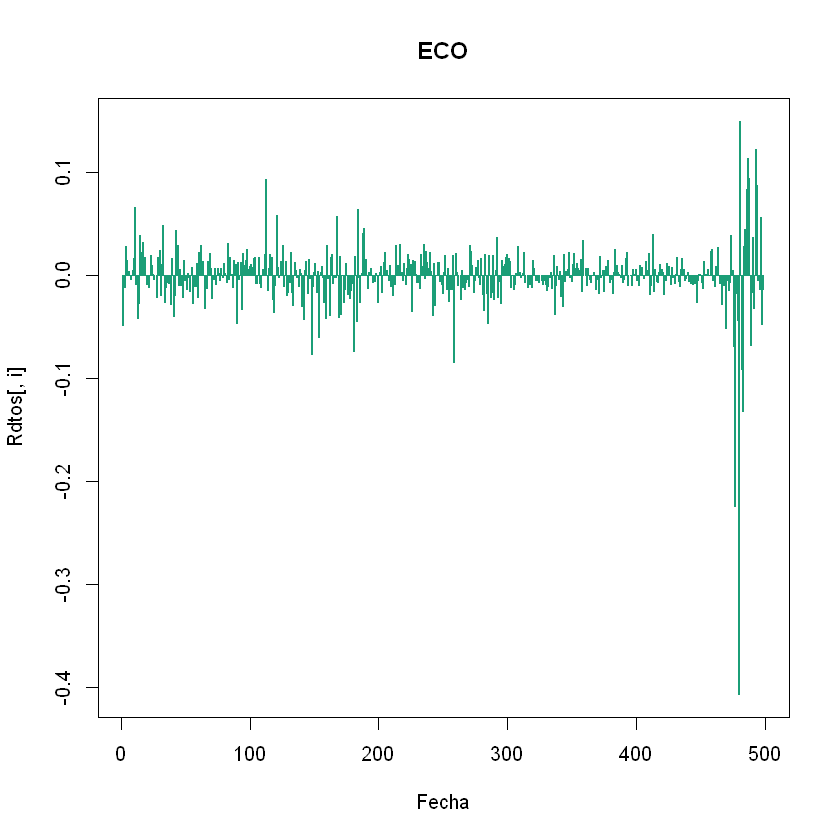
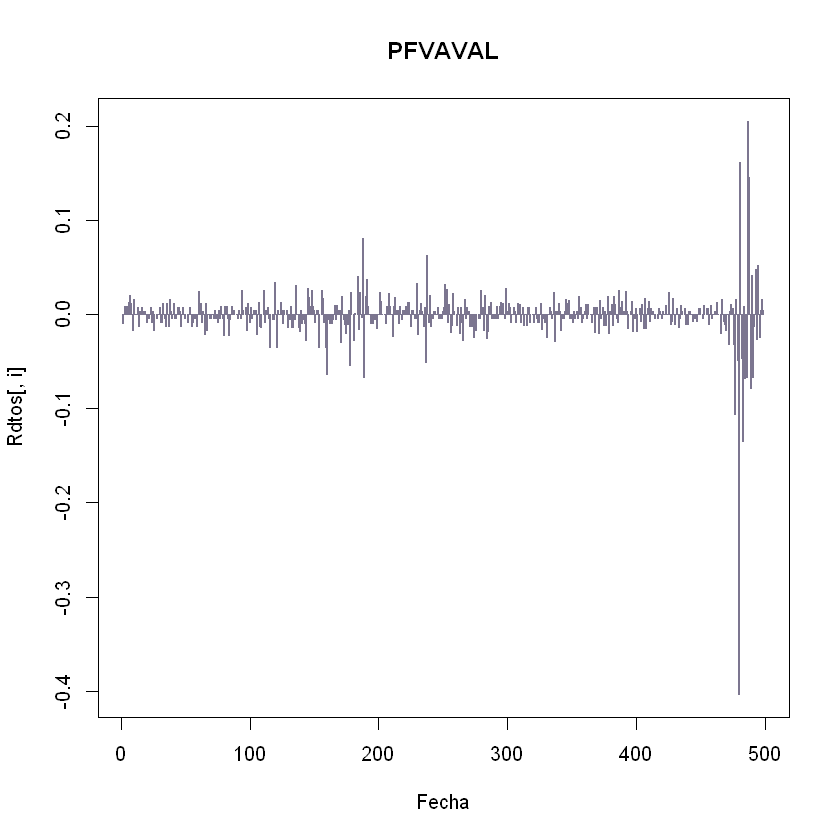
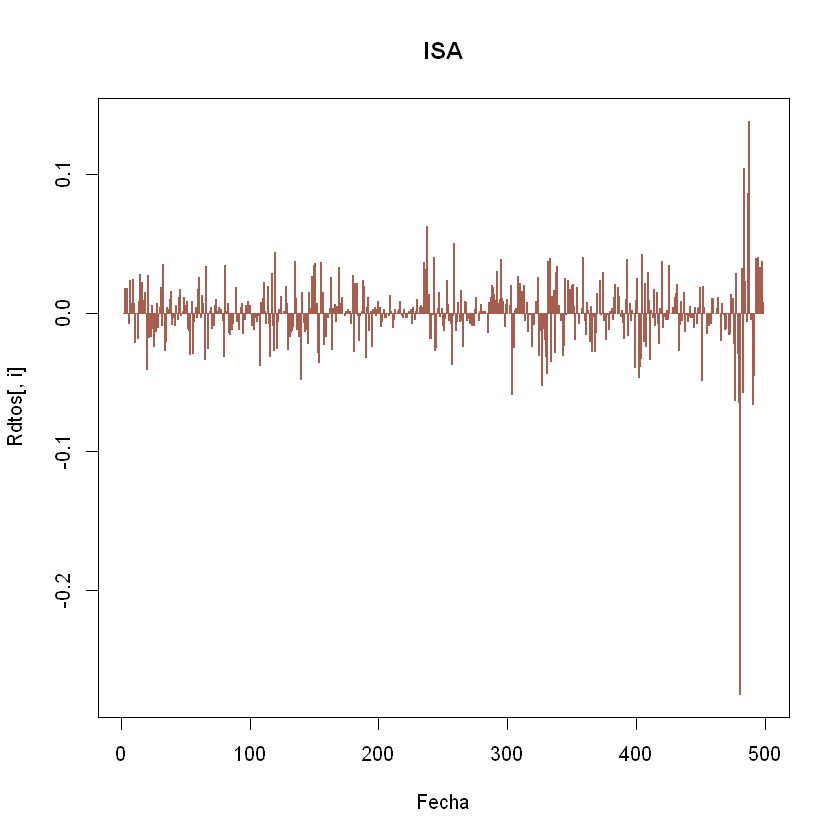
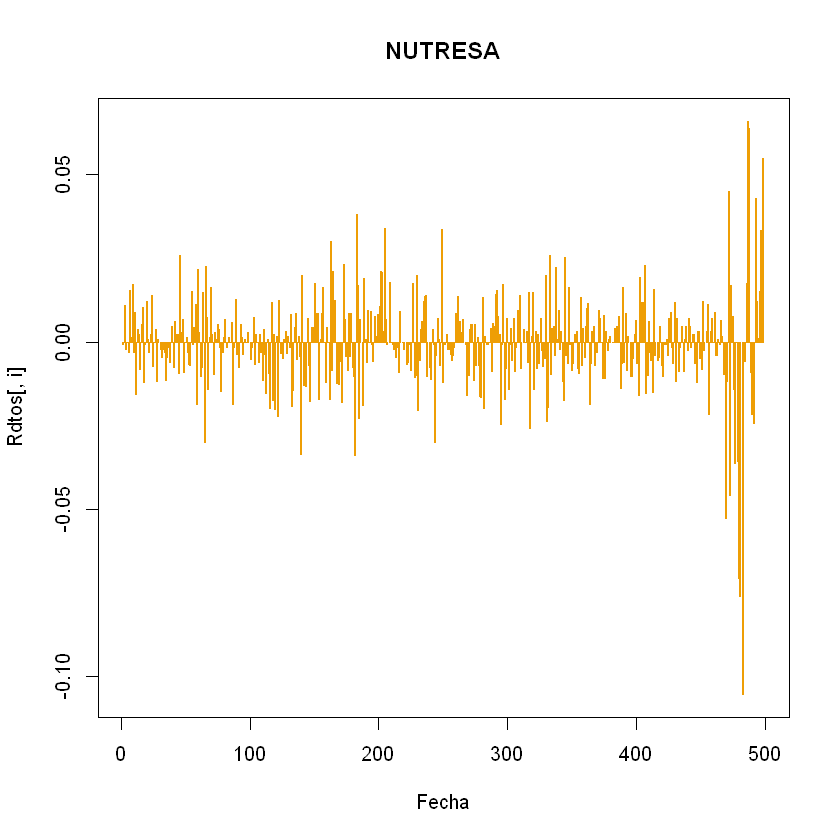
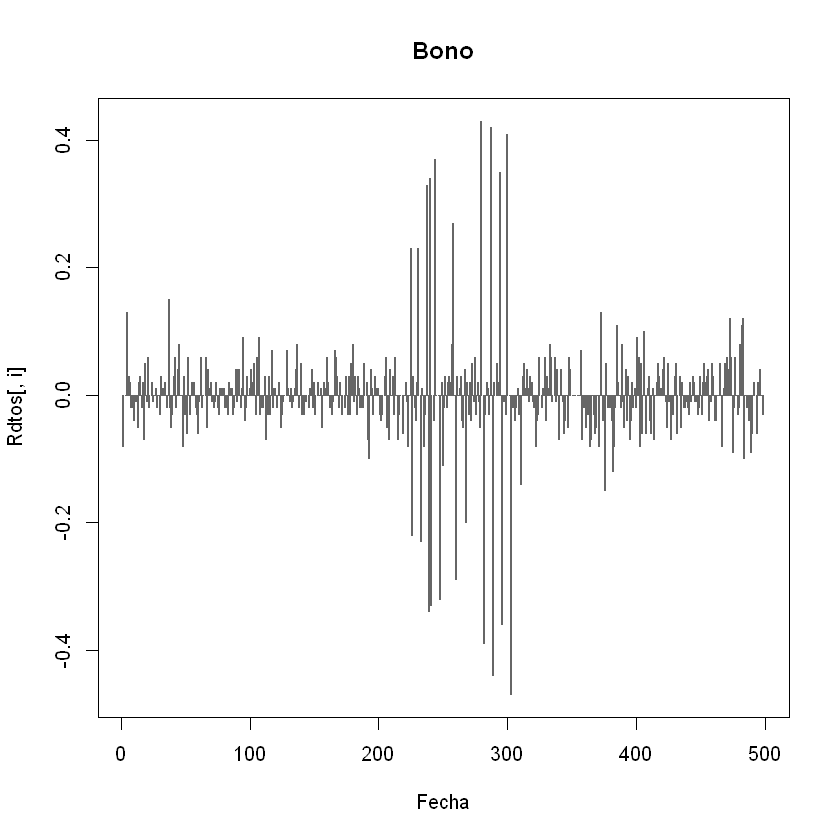
Tal como se indicó en Obtención y Análisis de Rendimientos R, se sacan las estadisiticas básicas de los rendimientos de los activos que compondrán el portafolio.
#estadisticas básicas
summary(Rdtos)
#medias y volatilidades
media_rdto=apply(Rdtos,2,mean)
media_rdto
volatilidades=apply(Rdtos,2,sd)
volatilidades
#matriz de covarianzas
covarianza= cov(Rdtos)
covarianza
ECO PFVAVAL ISA
Min. :-0.4065868 Min. :-0.4038136 Min. :-0.2756262
1st Qu.:-0.0096853 1st Qu.:-0.0077445 1st Qu.:-0.0084889
Median : 0.0000000 Median : 0.0000000 Median : 0.0012674
Mean :-0.0004481 Mean :-0.0003991 Mean : 0.0006411
3rd Qu.: 0.0116560 3rd Qu.: 0.0081301 3rd Qu.: 0.0101585
Max. : 0.1498123 Max. : 0.2058521 Max. : 0.1386834
NUTRESA Bono
Min. :-0.1053605 Min. :-0.4700000
1st Qu.:-0.0063179 1st Qu.:-0.0300000
Median : 0.0000000 Median : 0.0000000
Mean :-0.0002686 Mean :-0.0008032
3rd Qu.: 0.0053323 3rd Qu.: 0.0200000
Max. : 0.0659826 Max. : 0.4300000
- ECO
- -0.000448079420309658
- PFVAVAL
- -0.000399126557267209
- ISA
- 0.000641139381259261
- NUTRESA
- -0.000268581506343462
- Bono
- -0.000803212851405623
- ECO
- 0.0319931869227726
- PFVAVAL
- 0.0286517789360445
- ISA
- 0.0237607910031427
- NUTRESA
- 0.014037247290808
- Bono
- 0.0807544744305989
| ECO | PFVAVAL | ISA | NUTRESA | Bono | |
|---|---|---|---|---|---|
| ECO | 0.0010235640 | 5.915563e-04 | 1.172116e-04 | 1.505284e-04 | 1.807730e-05 |
| PFVAVAL | 0.0005915563 | 8.209244e-04 | 1.555274e-04 | 1.313111e-04 | 7.803865e-05 |
| ISA | 0.0001172116 | 1.555274e-04 | 5.645752e-04 | 1.526683e-04 | -8.833299e-05 |
| NUTRESA | 0.0001505284 | 1.313111e-04 | 1.526683e-04 | 1.970443e-04 | -7.410628e-05 |
| Bono | 0.0000180773 | 7.803865e-05 | -8.833299e-05 | -7.410628e-05 | 6.521285e-03 |
Optimización del portafolio con activo de renta fija.
Ingresar un activo de enta fija a un portafolio no supone mayores cambios en la optimización, por tanto, se procede de manera similar al caso de portafolio solo con renta variable, tal como se procedió en Optimización de portafolios. Se debe tener en cuenta que en este caso, se está ultilizando activos colombianos por tanto, se debe utilizar una tasa libre de riesgo que corresponda a un Bono a 10 años de Colombia, nuvamente convertida a un valor diario.
Con esto, se obtendrá una frontera eficiente que contiene un activo libre de riesgo de crédito por lo que podrá reducir el riesgo del portafolio.
#optimización del portafolio
library(fPortfolio)
rf=0.000029 #cambiar por la tasa libre de riesgo diaria para Colombia
espcartera=portfolioSpec()
`setRiskFreeRate<-`(espcartera, 0.000029) #cambiar por la tasa libre de riesgo diaria para Colombia
`setNFrontierPoints<-`(espcartera, 20)
constraints="longOnly"
#gráfico de la frontera eficiente
Frontera= portfolioFrontier(as.timeSeries(Rdtos[-1,]),spec = espcartera, include.mvl = TRUE, title = "Cartera")
Frontera
Model List:
Type: MV
Optimize: minRisk
Estimator: covEstimator
Params: alpha = 0.05
Portfolio List:
Target Weights: NULL
Target Return: NULL
Target Risk: NULL
Risk-Free Rate: 2.9e-05
Number of Frontier Points: 50
Optim List:
Solver: solveRquadprog
Objective: portfolioObjective portfolioReturn portfolioRisk
Options: meq = 2
Trace: FALSE
Model List:
Type: MV
Optimize: minRisk
Estimator: covEstimator
Params: alpha = 0.05
Portfolio List:
Target Weights: NULL
Target Return: NULL
Target Risk: NULL
Risk-Free Rate: 0
Number of Frontier Points: 20
Optim List:
Solver: solveRquadprog
Objective: portfolioObjective portfolioReturn portfolioRisk
Options: meq = 2
Trace: FALSE
Title:
MV Portfolio Frontier
Estimator: covEstimator
Solver: solveRquadprog
Optimize: minRisk
Constraints: LongOnly
Portfolio Points: 5 of 49
Portfolio Weights:
ECO PFVAVAL ISA NUTRESA Bono
1 0.0000 0.1005 0.0000 0.0000 0.8995
13 0.0104 0.1176 0.0000 0.8172 0.0548
25 0.0232 0.0155 0.3245 0.6060 0.0308
37 0.0135 0.0000 0.6637 0.3021 0.0208
49 0.0000 0.0000 1.0000 0.0000 0.0000
Covariance Risk Budgets:
ECO PFVAVAL ISA NUTRESA Bono
1 0.0000 0.0029 0.0000 0.0000 0.9971
13 0.0114 0.1352 0.0000 0.7634 0.0900
25 0.0184 0.0120 0.4408 0.5095 0.0193
37 0.0056 0.0000 0.8437 0.1473 0.0034
49 0.0000 0.0000 1.0000 0.0000 0.0000
Target Returns and Risks:
mean Cov CVaR VaR
1 -0.0006 0.0728 0.1799 0.0712
13 -0.0003 0.0137 0.0327 0.0190
25 0.0000 0.0143 0.0346 0.0184
37 0.0003 0.0182 0.0416 0.0225
49 0.0006 0.0238 0.0532 0.0314
Description:
Thu May 21 20:57:27 2020 by user: Natalia
Gráfico de la frontera
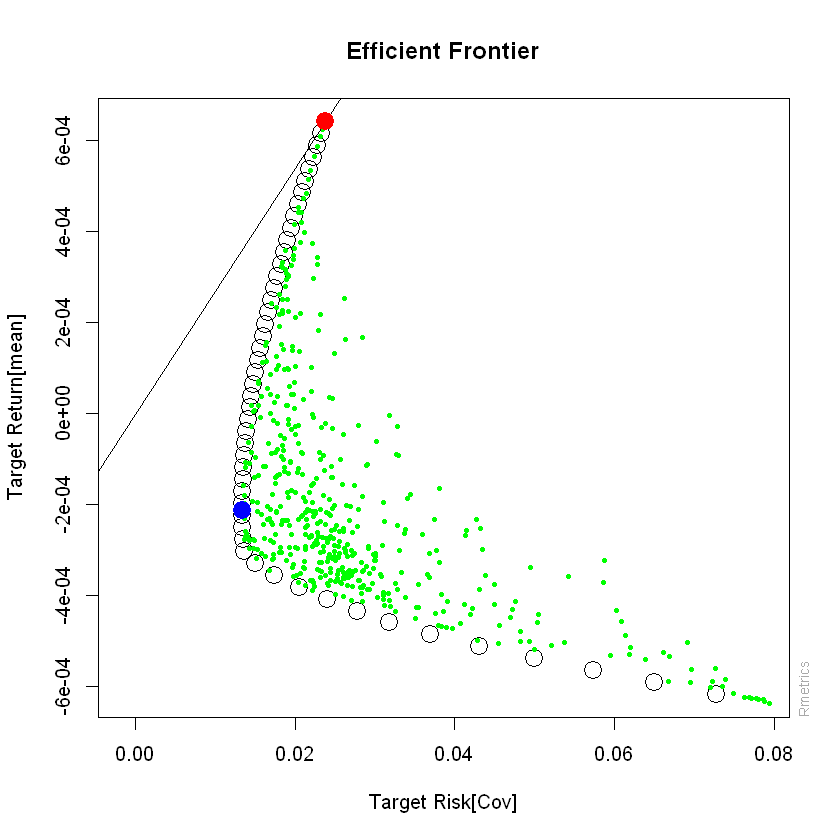
Al igual que en código presentado para Optimización de portafolios. Se crea la frontera eficiente; sin embargo, en este caso puntual no exite un portafolio tangente debido al comportamiento bajista de las acciones en los últimos 6 meses, Por tanto, en este caso no se crea línea del Mercado de Capitales. Si la media de los rendimientos de sus acciones tienen rendimiento positivo, existirá punto tangencial.
frontierPlot(Frontera, frontier = "both", col = c("black", "black"), cex=2)
monteCarloPoints(Frontera, col= c("green", "green"), mcSteps = 500, cex=0.5, pch = 19)
tangencyLines(Frontera)
minvariancePoints(Frontera, col="blue", pch=19, cex=2)
tangencyPoints(Frontera, col="red", cex= 2, pch=19)
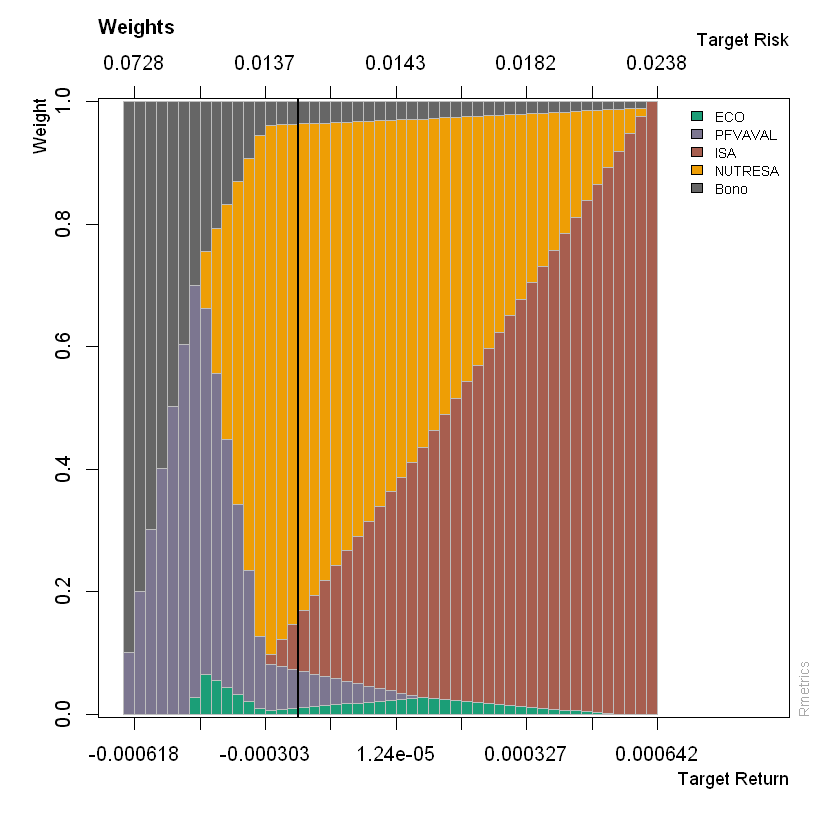
# Gráfico de los pesos del portafolio
col= qualiPalette(ncol(Rdtos), "Dark2")
weightsPlot(Frontera, col=col)
Análisis del portafolio
Al incluir un activo libre de riesgo en el portafolio, se espera reducir el riesgo para el inversionista, por lo que en un portafolio con renta fija, se debe escoger el portafolio de mínima varianza, ya que bajo esta lógica, no convendría aumentar el riesgo del inversionista escongiendo el portafolio tangente.
El portafolio eficiente, se determina similar al de la sección Análisis y Selección de Portafolios
# portafolio eficiente o de mínima varianza punto azul (cartera conservadora)
Portafolio_Efi= efficientPortfolio(as.timeSeries(Rdtos[-1,]),spec = espcartera,constraints)
Portafolio_Efi
W_efi=getWeights(Portafolio_Efi)
Title:
MV Efficient Portfolio
Estimator: covEstimator
Solver: solveRquadprog
Optimize: minRisk
Constraints:
Portfolio Weights:
ECO PFVAVAL ISA NUTRESA Bono
0.0104 0.0617 0.0853 0.8056 0.0370
Covariance Risk Budgets:
ECO PFVAVAL ISA NUTRESA Bono
0.0104 0.0617 0.0853 0.8056 0.0370
Target Returns and Risks:
mean Cov CVaR VaR
-0.0002 0.0134 0.0325 0.0177
Description:
Thu May 21 20:57:39 2020 by user: Natalia
Similar al ratio de Sharpe visto en Análisis y Selección de Portafolios se determina nuevamente, para este nuevo portafolio de instrumentos colombianos
#Ratio Sharpe:
Rport_efi=getTargetReturn(Portafolio_Efi)
Riskport_efi= getTargetRisk(Portafolio_Efi)
sigma_efi=Riskport_efi[2]
Sharpe_efi=(Rport_efi[2]-rf)/sigma_efi
Sharpe_efi
Y el gráfico de torta donde se especifica la composisición de la cartera se realiza de igual forma que en la sección Análisis y Selección de Portafolios
weightsPie(Portafolio_Efi, col= col, radius = 0.5)
mtext(text = "portafolio eficiente", side = 3, line = 1.5, font = 1, cex = 0.7, adj = 0)
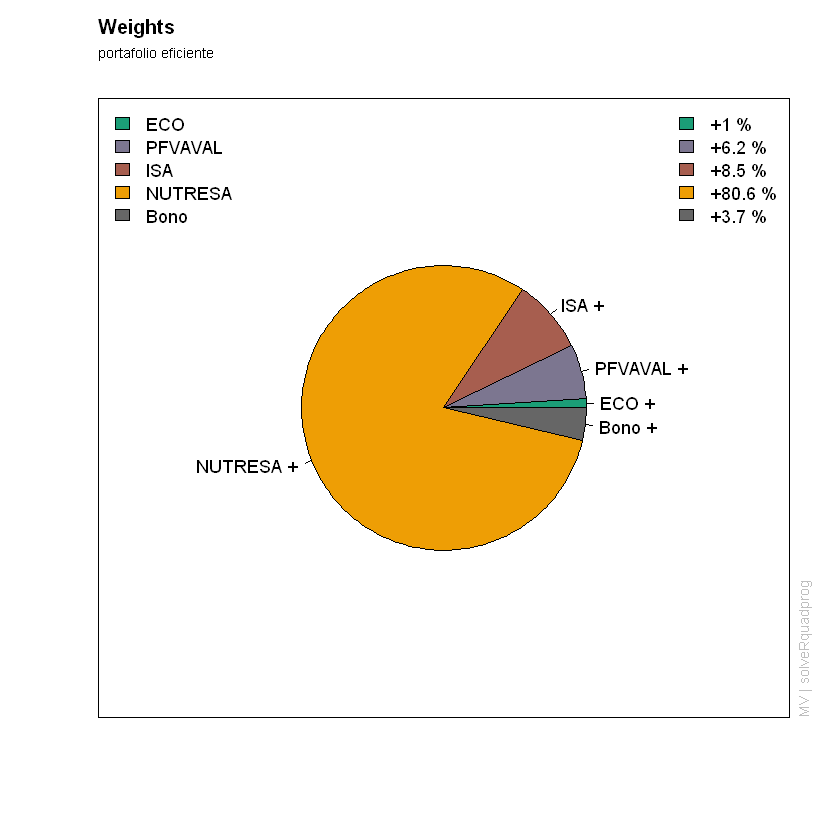
Desempeño del portafolio (Aplicación Trabajo Final)
Cuando se desea observar el desempeño histórico de un portafolio, este dependerá de la base de inversión con la que se esté configurando. En este caso particular, se quiere determinar el desempeño para un Fondo de Inversión Colectivo-FIC, por tanto, como se observan en la fichas técnicas de los FIC ver ejemplo aquí, el desempeño del portafolio de inversión esta determinado por una base llamada “valor de la unidad”.
Con el fin de representar este mismo escenario, se procede a crear un
valor de la unidad inicial valor_ini_unidad= 2000, este valor es
inventado en un monto de 2000. al ser multiplicado por los rendimientos
históricos del portafolio, creados en el objeto
rdto_port_efi= vector(), se podrá visualizar la evolución en el
tiempo del portafolio, es decir, el valor final que tiene el portafolio
basado en un valor inicial de 2000.
Hay que recordar que el valor final de un monto es igual a:
Por ello, se utiliza aplica la formula en
unidad[1]=valor_ini_unidad*(1+rdto_port_efi[1])
En mi caso, se puede observar que mi portafolio viene en una tendencia bajista.
#rendimiento histórico del portafolio
rdto_port_efi= vector()
for(i in 1:nrow(Rdtos)){
rdto_port_efi[i]= sum(Rdtos[i]%*%W_efi)
}
valor_ini_unidad= 2000
unidad=vector()
unidad[1]=valor_ini_unidad*(1+rdto_port_efi[1])
for (i in 2:nrow(Rdtos)) {
unidad[i]=unidad[i-1]*(1+rdto_port_efi[i])
}
plot(unidad, t="l", main= "Rendimientos del portafolio")
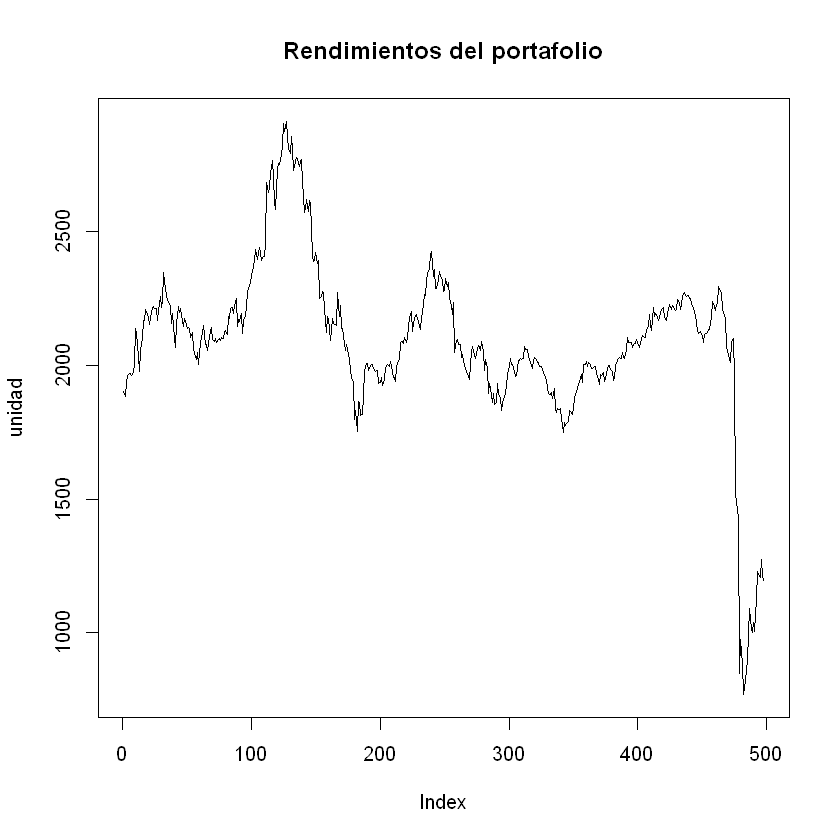
De este mismo análisis, se puede obtener el valor actual del portafolio
para este fondo, en este caso, se escoge el último valor del objeto
unidad= vector() Particularmente, el valor de la unidad de mi
portafolio descendió de un valor inicial de COP 2000 a un valor final de
COP 1196.78
#Valor de la unidad al final del portafolio
VF_unidad= tail(unidad,1)
VF_unidad