Escalamiento Multidimensional
Es una técnica de reducción de dimensiones que toma en cuenta las distancias entre cada par de elementos. En este caso, deseamos representar los n elementos en un sistema de coordenadas de baja dimensión, en el que las distancias entre los elementos coincidan estrechamente con las distancias originales.
Asumimos que existe una matriz de datos \(Y_{n×p}\) tal que las distancias entre dos objetos \(r\) y \(s\) es \(\delta_{rs} = |y_r − y_s|\). Como \(Y\) normalmente no se observa, tratamos de encontrar un conjunto de observaciones \(Z = [z_1,z_2,...,z_n]\) donde \(z_i\) está en un espacio k-dimensional tal que las distancias \(d_{rs} = |z_r − z_s|\) donde \(d_{rs}\approx \delta_{rs}\). Por lo tanto, un modelo para las distancias puede tomar la forma:
Escalamiento métrico clásico:
Aquí se parte de la idea que la relación entre las similitudes y las distancias tienen una relación lineal. El procedimiento implica transformar la matriz de similitudes en una matriz de distancias cumpliendo con los postulados de la distancia euclidiana:
No negatividad \(d_{ij}\geq 0 = d_{ii}\)
Simetría \(d_{ij}=d_{ji}\)
Desigualdad triangular \(d_{ij}\leq d_{ik}+d_{kj}\)
Simlitudes
Al cumplir las anteriores 3 propiedades se puede decir que la matriz es de similitudes \(C\) y que a apertir de ella se puede producir una matriz de distancias \(D\).
Para encontrar una solución, se estima una cosntante aditiva que cumpla con la propiedad 3 de la desigualdad triangular. A esto se le conoce como el cálculo de la constante aditiva. La cual es el mínimo valor de una constante \(c\) que verifique la desigualdad, así:
Las distancias se obtienen sumando las similitudes con constante \(c\), es decir, \(d_{ij}= \delta_{ij}+c\)
Ejemplo del cálculo de distancias a partir de las similitudes
Suponga que tiene la siguiente matriz de similitudes:
En este caso la matriz no cumple con la desiguadad triangular, ya que no cumple por ejemplo; \(\delta_{13} \leq \delta_{12}+\delta_{23}\) \(\left(5>1+2\right)\)
Por tanto calculamos el minimo \(c\):
la Matriz de distancias quedará así:
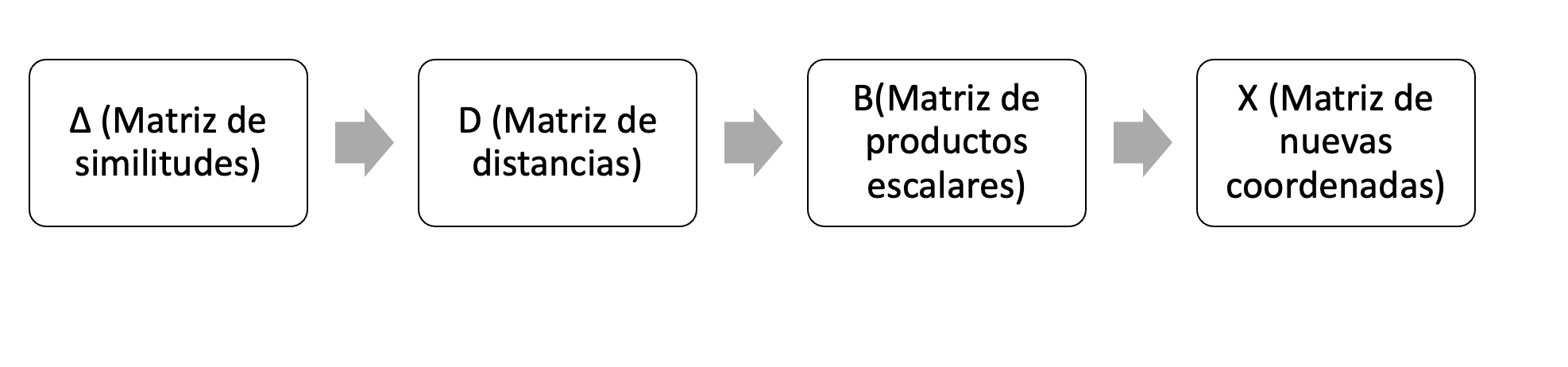
Una vez obtenida la matriz de distancias \(D\) es necesario hacer una tranformación líneal de productos escalares así:
donde:
\(d_i^2\) es la media de la distancia cuadrática por fila.
\(d_j^2\) es la media de la distancia cuadrática por columna.
\(d^2\) es la media de la distancia cuadrática de la matriz.
Al tener la matriz de distancia escalada se porcede al cálculo de las nuevas coordenadas en el de cada uno de los conjuntos de objetos (estímulos) en cada una de las dimensiones. Aquí utilizamos cualquier método de factorización para la nueva matriz \(B\) para que sea igual a \(XX'\)
no_metrico
Escalamiento no Métrico
Método de ordenación para datos no normales o que se encuentran en escalas diferentes, en este modelo se establece una relación monótona entre las similitudes y distancias dada por una función \(d_{ij}=f\left(\delta_{ij}\right)\). Aquí el problema de la desigualdad traingular no se produce.
En el escalamiento no métrico, la matriz \(\vartriangle\) en lugar de estar compuesta por similitudes medidas, se basa en percepciones o juicios sobre un conjunto de objetos (estímulos). Por lo tanto, se sabe que un objeto se percibe como mejor que otro, pero no se puede decir en qué medida. En estas situaciones, solo se pueden ordenar las medidas de similitud como se observa en la imagen.

distancia_vs_similaridad
Procedimiento para Escalamiento Multidimensional no Métrico
Este método contempla un proceso determinados por una serie de momentos que terminan en n proceso iterativo
Se transforma la matriz de similitudes en rangos: se le asigna una desemejanza menor al rango 1; la subsiguiente tendrá asignado el rango 2, y así, hasta llegar al mayor rango que \(n(n-1)/2\)
Matriz de coordenadas: Se obtienen una matriz \(X\) de coordenadas aleatorias, que calcula las distancias entre estímulos.
Calcular las disimilitudes, por medio de distancias euclideas. a estas nuevas distancias se le conocen como disparidades y son obtenidas por una regresión Monótona.
Regresión Monotónico o Isotónica: Modelo para ajustar una línea con forma libre sobre una secuencia de observaciones, la línea ajustada es creciente en todas partes.
Defininición del Stress: es la suma cuadrática de los errores producidos para todos los pares \(\left(i,j\right)\)
Minimización del Stress se repetirá el proceso hasa encontrar el mínmo Stress (gradiente descendente)
Stress
Sirve como medida de bondad de ajuste del modelo de escalamiento.
Se obtien la medidade no ajuste o no monotonía a lo que se le conoce como Stress bruto.
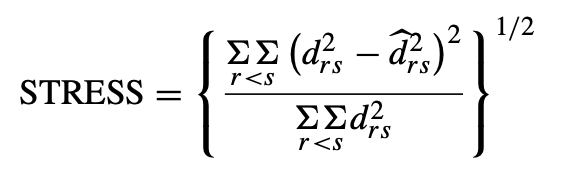
stress
La métrica se encuentra entre 0 y 1, el máximo Stress permitido será de un 10%, para considerar que el ajuste es aaceptable, y representa una buena similitud.
Stress mínimo x 100% |
Bondad de Ajuste |
|---|---|
20 |
pobre |
10 |
Aceptable |
5 |
bueno |
2.5 |
Excelente |
0 |
Perfecto |
Mientras mayor sea la diferencia entre las disparidades y las distancias, es decir, entre \(f(\delta_{ij})\) y \(d_{ij}\), mayor será el Stress
Todos los paquetes estadísticos tienen paquetes reiterantes con el fin de alcanzar la mejor solución posible