Escalamiento Multidimensional el R

Si se cuenta con multiples variables que describen las caracteristicas del problema pero se desea reducir la dimensionalidad, tal como pasaba con componentes principales o análisis factorial, pero esta vez tomando en cuenta la similitudes de los datos (como en clustering), puede hacer uso del escalamiento multidimensional. Se puede implementar tanto métrico como no métrico.

Métrico clásico:

Se busca conservar las distancias métricas originales, es el método recomendado para usarse con variables cuantitativas. También se conoce como el método de coordenadas principales.

En R, podemos utilizar las funciones cmdscale() de la librería {stats} o también se puede hacer desde isoMDS() y sammon()del paquete {MASS}

Leemos los datos, la BD utilizada es “EAM_2019_group.csv”

datos <- read.csv("EAM_2019_group.csv", sep = ",", dec = ",", header = T)
print(head(datos))

     X datos.gasto_personal datos.costos_gastos_produccion datos.ventas
1011              1459203                         177274     18565287
1020               814349                        3566733     20658258
1030              7334998                        5941761    115741258
1040              4959474                        4536304     90612765
1051              9352991                        6846304    192609248
1061              3720876                        3799372    306175590
  datos.inversion_AF
           649040
          1389081
          5615593
          1325824
          4979745
          9086434

Los datos deben contener etiquetas por lo que se le asigna a las filas los nombres de la primera columna

row.names(datos) <- datos$X
datos$X <- NULL

print(str(datos))

'data.frame':       60 obs. of  4 variables:
 $ datos.gasto_personal          : int  1459203 814349 7334998 4959474 9352991 3720876 47892609 11081213 21648490 10934460 ...
 $ datos.costos_gastos_produccion: int  177274 3566733 5941761 4536304 6846304 3799372 44427434 1843527 12959271 16959038 ...
 $ datos.ventas                  : int  18565287 20658258 115741258 90612765 192609248 306175590 388005721 26727389 260836023 136493373 ...
 $ datos.inversion_AF            : int  649040 1389081 5615593 1325824 4979745 9086434 42426113 50853587 5970883 11555678 ...
NULL

Calculamos las distancias Euclideas:

dist <- dist(datos, method = "euclidean")

Se ajusta el modelo de escalamiento métric, partiendo de las disimilitudes hasta llegar a un conjunto de coordenadas principales:

escalado <- cmdscale(dist)

Por defecto la función genera 2 grupos, existen autores que no recomiendan usar mas de 2, sin embargo, hay opiniones como Kruskal en 1964, que indica que máximo 9 dimensiones pueden ser usadas. la principal ventaja de este modelo su adpatabilidad a las necesidades del problema.

print(head(escalado))

          [,1]      [,2]
-78710541  -2693081
-76399117  -1226945
18905169  -5253596
-6616521  -7426404
95360889 -13430884
207837628 -25576966

Visualización de las nuevas coordenadas

library(ggrepel)

Warning message:
"package 'ggrepel' was built under R version 4.1.3"
Loading required package: ggplot2

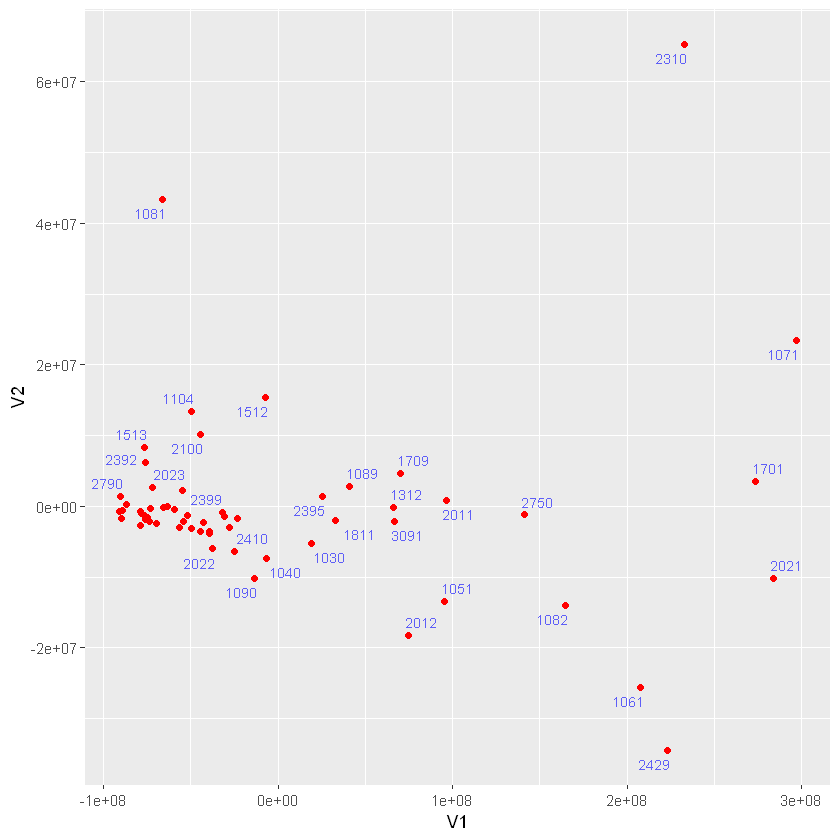
cmd_eam <- as.data.frame(escalado) #crea el dataframe, a partir de datos escalados

g1 <- ggplot(cmd_eam, aes( x = V1,
                     y = V2,
                     label = rownames(datos)))+
          geom_point(color = "red")+
          geom_text_repel(alpha = 0.6, size = 3, col = "blue") #grafica sin solapar los textos (omite los datos solapados)
print(g1)

Warning message:
"ggrepel: 32 unlabeled data points (too many overlaps). Consider increasing max.overlaps"

Escalamiento no métrico:

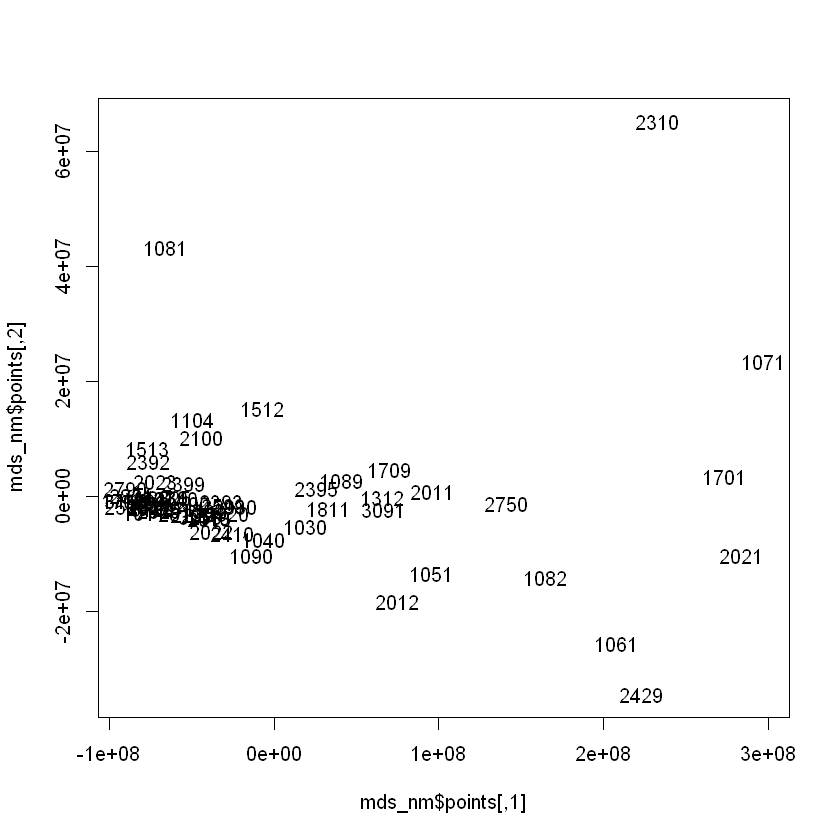
La función isoMDS() porporciona el algoritmo para realizar escalamiento no métrico, sin embargo, si no le se proporciona la función de rangos de los datos, realizará su solución por medio del método clásico cmdscale(). Por tanto, el resultado será el mismo, ya que k=2 por defecto.

library(MASS)

mds_nm <- isoMDS(dist) #ajusta el modelo clásico a la matriz de distancias.
plot(mds_nm$points, type = "n")
text(mds_nm$points, rownames(mds_nm$points))

initial  value 1.881156
final  value 1.881156
converged

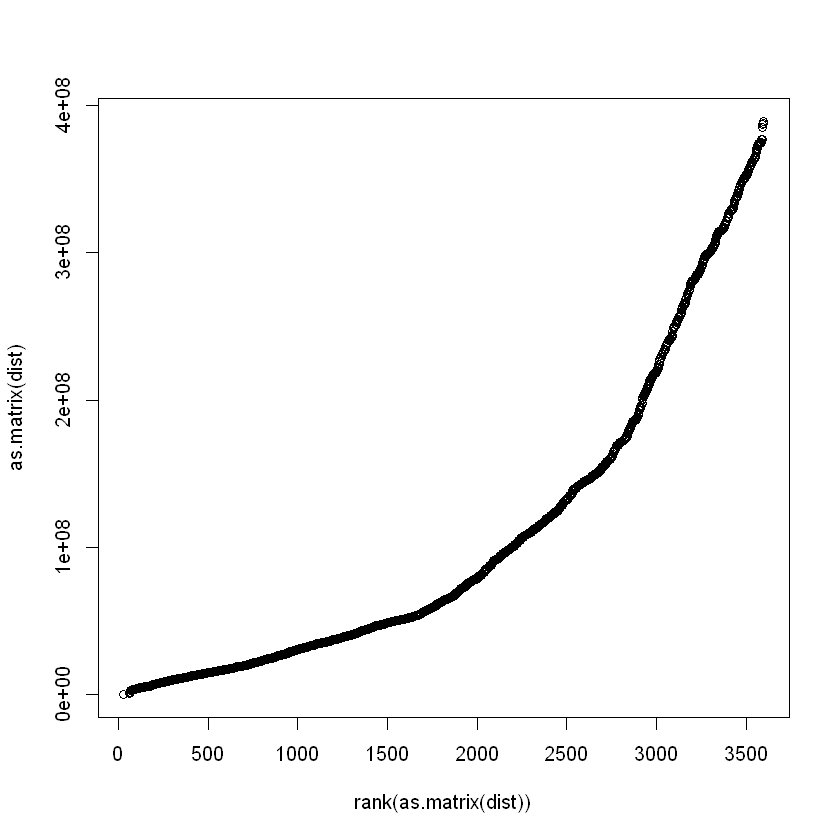
Para cambiar esta solución, debe realizarse el ranking u ordenamiento de las variables. la función rank()de la base, proporciona esta salida.

plot(rank(as.matrix(dist)), as.matrix(dist)) #la función Rank ordena las distancias como una sequiencia

empresa_rank <- matrix((rank(as.matrix(dist))), nrow = nrow(datos))# convierte en matriz
mds_nmrk2 <- isoMDS(empresa_rank)  #aplica EMD a los datos ordenados

initial  value 12.063241
final  value 12.063215
converged

Visualizando el nuevo agrupamiento:

modelk2 <- as.data.frame(mds_nmrk2$points)#convierte la salida en DF para ser usada en ggplot2

g2 <- ggplot(modelk2, aes(x = V1,
                   y = V2,
                   label = rownames(datos)))+
          geom_point(color = "red")+
          geom_text_repel(alpha = 0.6, size = 3, col = "blue")

print(g2)

Warning message:
"ggrepel: 17 unlabeled data points (too many overlaps). Consider increasing max.overlaps"

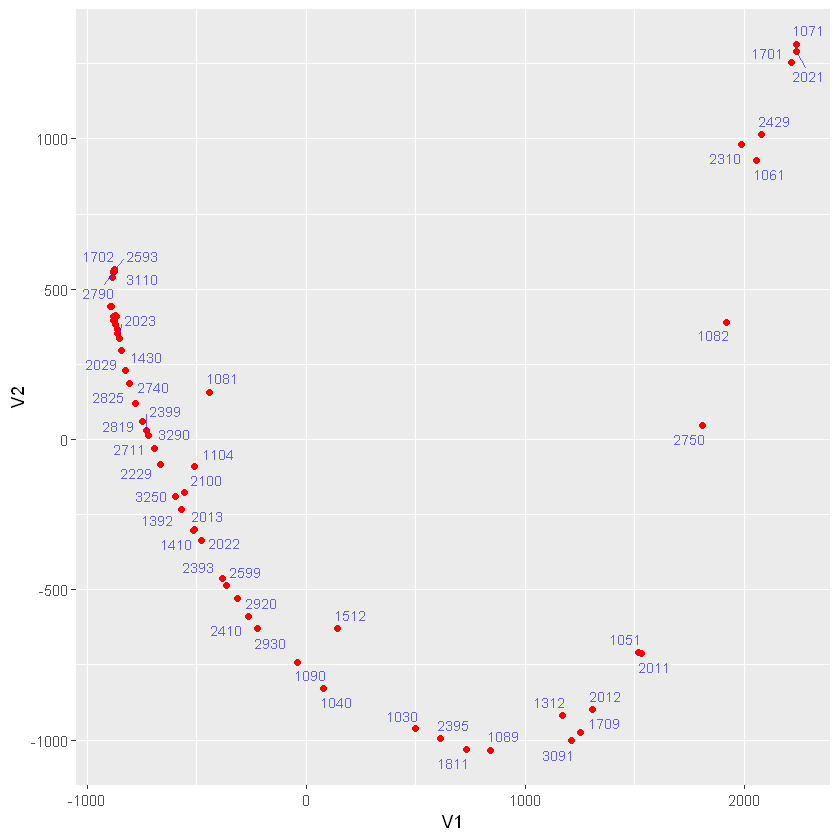
Diferencia entre métrico y no métrico

Se puede observar como el agrupamiento toma un orden dentro los dos rangos.

library(gridExtra)
grid.arrange(g1, g2, ncol = 2)

Warning message:
"package 'gridExtra' was built under R version 4.1.3"
Warning message:
"ggrepel: 35 unlabeled data points (too many overlaps). Consider increasing max.overlaps"
Warning message:
"ggrepel: 17 unlabeled data points (too many overlaps). Consider increasing max.overlaps"

Determinar el K óptimo:

Similar a los gráficos de sedimentación realizados en los otros modelos, se espera escoger aquel que modelo que lo minimice. Para ello se realiza el ajuste de diferentes K, donde se evalua el punto donde se logre estabilidad. Recuerde que según la teoría no es recomendable, realizar mas de 9 dimensiones.

#Ajuste para cada K en los datos ordenados
mds_nmrk1 <- isoMDS(empresa_rank,k=1)
mds_nmrk2 <- isoMDS(empresa_rank) #por defecto usa K=2
mds_nmrk3 <- isoMDS(empresa_rank, k=3)
mds_nmrk4 <- isoMDS(empresa_rank, k=4)
mds_nmrk5 <- isoMDS(empresa_rank, k=5)
mds_nmrk6 <- isoMDS(empresa_rank, k=6)

initial  value 19.798271
final  value 19.798202
converged
initial  value 12.063241
final  value 12.063215
converged
initial  value 11.765570
final  value 11.765554
converged
initial  value 9.928388
final  value 9.928374
converged
initial  value 9.172647
final  value 9.172632
converged
initial  value 7.040586
final  value 7.040566
converged

Gráfico de sedimentación del STRESS

stress = c(mds_nmrk1$stress, mds_nmrk2$stress, mds_nmrk3$stress, mds_nmrk4$stress, mds_nmrk5$stress, mds_nmrk6$stress)
dimensions = 1:6
plot(dimensions, stress, type = "b", xlab = "Number of Dimensions", ylab = "Stress")
print(stress)

[1] 19.798202 12.063215 11.765554  9.928374  9.172632  7.040566