Teoría Análisis Factorial
El Análisis Factorial es un método estadístico que se utiliza para descubrir estructuras latentes que hipotéticamente pueden subyacer a la covarianza o correlación entre variables típicamente observadas de forma continua.
Existe una similitud entre el Análisis de Componentes Principales (ACP) y el Análisis Factorial, ya que ambos procuran por extraer características comunes de los datos observados y pretenden reducir la dimensionalidad de los datos. Sin embargo, existen diferencias marcadas en el concepto del Análisis Factorial. Mientras que el Análisis de Componentes Principales busca generar combinaciones lineales de variables aleatorias observadas, en el Análisis Factorial, son las variables observadas las que se hipotetizan como combinaciones lineales de factores subyacentes hipotéticos. Mientras que la prioridad del ACP era explicar la mayor cantidad posible de la varianza total de las variables, la prioridad del Análisis Factorial es explicar la covarianza o correlación, o más generalmente, la similitud entre las variables.
Específicamente, en el Análisis Factorial podemos buscar variables que se encuentren correlacionadas entre sí, para determinar que pertenecen a algún grupo.
La relación entre variables es expresada por el :math:`r^2` coeficiente de determinación que sería la correlación de Pearson al cuadrado, esto explica la varianza común o conjunta, es decir, si dos variables tienen un 0.9 de correlación su varianza conjunta será:
Para analizar solo las varianzas comunes de las variables, se debe sustituir de la matriz de correlaciones los \(1\) que se muestran en la diagonal, por las varianzas en común que cada ítem con los demás. A este proceso se le conoce como estimación de las comunalidades, y no hay un cálculo único para hacerlo.
Si le damos un vistazo a la siguiente salida de un Análisis Factorial de algunas variables, podremos observar lo expresado:
Variable |
Factor 1 |
Factor 2 |
|---|---|---|
Percepción visual |
0,354 |
0,376 |
Cubos |
0,232 |
0,219 |
Pastillas |
0,3664 |
0,293 |
Comprensión de párrafos |
0,866 |
0,112 |
Completar oraciones |
0,794 |
0,205 |
Significado de palabras |
0,815 |
0,114 |
Adición |
0,126 |
0,624 |
Contar puntos |
0,864 |
|
Interpretación líneas-curvas |
0,288 |
0,635 |
En la tabla anterior, se pueden observar los factores hipotéticos creados como una combinación lineal de la varianza de las variables, desde el punto de vista contextual, podemos decir que se tratan de constructos hipotéticos extraídos por el procedimiento de Análisis Factorial. Cada una de las columnas, muestran la correlación entre las variables y cada factor hipotético, por tanto, podemos asumir que por ejemplo; las variables compresión de párrafos, completar oraciones, y significado de palabras se pueden agrupar en el Factor 1, ya que las mayores correlaciones se encuentran en él, y las variables adición, contar puntos e interpretación de líneas podrían pertenecer o explicar al Factor 2. Desde el punto de vista interpretativo, podemos decir que el modelo de Análisis Factorial creó dos factores que reducen la dimensionalidad del problema a explicarse por ejemplo por las variables que comprenden la compresión lectora y las que comprenden el análisis gráfico. Con respecto a las demás variables se puede decir que no explican la suficiente correlación o covarianza a ninguno de los factores (podrían ser descartables o a decisión del investigador ingresarlas al factor que mayor relación tenga).
Para tener mas clara la interpretación dentro de los factores, podemos decir que los pesos pueden ser grandes o pequeños, positivos o negativos y en cada factor serán los pesos grandes los que definen al factor, sin importar su relación, es decir que en la matriz de carga de los factores aquellos con mayor valor absoluto serán los que definan el factor.
El modelo tradicionalmente asumido en la mayoría de los trabajos analíticos factoriales exploratorios es el siguiente, generalmente denominado modelo analítico factorial común:
Donde \(X\) es un vector de variables aleatorias que se asumen observables, \(\mu\) es el vector de medias para las variables aleatorias en \(X\), \(\Lambda\) es una matriz de carga de los factores (Scores), \(f\) es un vector de factores no observados y ε es el vector de la variación no explicada por \(\mu+\Lambda f\).
Si descomprimimos el modelo para \(p\) variables y \(m\) factores tendremos:
\(x-\mu=\Lambda f+\varepsilon\)
\(X_1-\mu_1=L_{11}f_1+L_{12}+...+L_{1m}f-m+\varepsilon_1\)
\(X_2-\mu_1=L_{21}f_1+L_{22}+...+L_{2m}f_m+\varepsilon_2\)
.
.
.
\(X_p-\mu_p=L_{p1}f_1+L_{p2}+...+L_{pm}f_m+\varepsilon_1\)
Note que el modelo es similar a una regresión
Supuestos del análisis factorial
Como en cualquier modelo estadístico, los supuestos son relevantes para este caso los que se deben cumplir son:
La media del vector latente \(f\) es igual a 0. Es decir, \(E(f) = 0\).
Los factores no covarían. Es decir, en una matriz de covarianza de factores estimados, esperaríamos que las covarianzas por pares entre los factores fueran iguales a cero (ortogonalidad). La matriz de covarianza de factores que esperaríamos sea una matriz identidad.
Los errores en el modelo son iguales a 0. Dado que la matriz de errores, \(\varepsilon\), es un vector aleatorio, la suposición es que \(E(\varepsilon) = 0\). Esta suposición es similar a la suposición del término de error en el modelo clásico de regresión múltiple.
Suponemos que los errores y las varianzas específicas en ε, no covarían. Es decir, la variación no explicada de cada variable observada no tiene nada en común con la variación no explicada de otra variable observada. Se espera entonces que el producto punto de los errores sea igual a:
Finalmente, se asume que el factor estimado y su varianza específica (o “única”) no varían. Es decir, \(E(\varepsilon f) = 0\). La suposición análoga en la regresión (aunque incorporando una variable “observada” en lugar de una latente) es que \(E(\varepsilon x) = 0\), es decir, la covarianza entre el término de error y el predictor variable es igual a 0.
Estimación de Parámetros en Análisis Factorial
Al igual que en otros modelos estadísticos, en AF requerimos estimar parámetros, la estimación puede hacerse por diversos métodos, sin embargo, solo examinamos dos, el de factor principal (o factorización del eje principal) y el de máxima verosimilitud, ya que son los más utilizados.
Método de extracción por Factorización del eje principal o Factor Principal:
También conocido como el método Bartlett es un método común para estimar factores es el del factor principal. Esta es una técnica de estimación de mínimos cuadrados y cumple su función minimizando los mínimos cuadrados no ponderados o los mínimos cuadrados ordinarios de la matriz residual. En este método, las comunalidades iniciales se estiman y se ingresan en la diagonal de la matriz de covarianza o correlación. Por ejemplo, considere la siguiente matriz de correlación en cinco variables observadas:
Una inspección visual inicial revela que las variables 1 y 3 están altamente correlacionadas (0,96) junto con las variables 2 y 5 (0,85) y 4 y 5 (0,79). Otras correlaciones bivariadas son bastante pequeñas, por ejemplo, 1 y 2 (0,02), así como 1 y 5 (0,01)
Recuerde que, en el ACP, los valores de 1,0 aparecían a lo largo de la diagonal de la matriz de correlación para indicar que cada variable contribuía con 1 unidad de varianza al problema. Dado que el Análisis Factorial normalmente está interesado en analizar la similitud en lugar de la varianza total, estos números a lo largo de la diagonal principal serán diferentes en Análisis Factorial que en PCA.
La factorización del eje principal reemplaza estos 1 con estimaciones iniciales de comunalidad antes de estimar los parámetros relevantes. Un estimador popular para estos elementos diagonales en la matriz de correlación es:
Donde \(h^2_i\) es la comunalidad estimada para la variable \(i\), \(R^2_i\) es el coeficiente de Determinación para la variable \(i\) en regresión sobre todas las demás variables observadas, y \(r^{ii}\) es el i-ésimo elemento diagonal de la inversa de la matriz de correlación \(R\).
La comunalidad de una variable dada se estima utilizando todas las demás variables en el conjunto de datos para predecir la variable en consideración. De esta manera, estamos interesados en saber cuánta varianza de la variable dada se comparte con otras variables en el conjunto.
Por otra parte, si se analiza la matriz de covarianza \(S\) en lugar de la matriz de correlación, un estimador apropiado es \(h^2_i = ss_{ii}R^2_i\)
Donde \(ss_{ii}\) es ahora el i-ésimo elemento diagonal de \(S\).
La principal desventaja de este modelo es que en ocasiones no proporciona convergencia ni una solución para los factores, sobre todo si se trata de muestras pequeñas.
También están disponibles otras formas de estimar las comunalidades; sin embargo, el punto clave a retener es el concepto de que estos números se estiman como un “punto de partida” para realizar el análisis factorial. Las comunalidades estimadas, en cierto sentido, inician el procedimiento analítico factorial.
Método de extracción: Máxima Verosimilitud:
Uno de los métodos más comunes para estimar parámetros en el contexto del Análisis Factorial es el de estimación por máxima verosimilitud. Recordemos que este es un mecanismo para la estimación de parámetros que hace a los datos observados los más probables de ocurrir, ya que define una distribución de probabilidad que depende de la muestra.
Cuando se tiene un modelo o una variable que se genera por datos normales, se estiman sus parámetros con el Logarítmo de la verosimilitud, por tanto, el estimador correcto en este caso está dado por:
Comparación de los métodos de extracción:
Algunos aspectos a tener en cuenta cuando se debe elegir el metodo de extracción son los siguientes:
Cuando existen comunalidades altas \((>0,6)\) todas las técnicas de extracción tienden a expresar la misma solución
Cuando las comunalidades son bajas el ACP tiende a brindar solución diferente al resto.
Cuando existe un numero alto de variables \((>30)\) las comunalidades influyen menos, así que todos los métodos tienen a dar la misma solución
Si el número de variables es bajo afectará la comunalidad por lo que dependará del método de estimación. *. Siempre será mas robusto utilizar un modelo
Metodos de rotación de factores:
La interpretación de la solución extraída resulta difícil cuando nos preguntamos si se define o no los factores verdaderos. La rotación de factores es un procedimiento utilizado con el fin de facilitar la interpretación de factores derivados con el fin de encontrar una estructura más simple.
Para entender el concepto de rotación, primero, se debe tener claro el concepto ortogonalidad,
Tengamos en cuenta que una matriz \(X\) es ortogonal si cumple con la siguiente condición:
Cuando se introduce una matriz ortogonal en el modelo factorial original, podemos producir la misma matriz de covarianza que antes. Por esta razón, la rotación de factores en el análisis factorial es permisible porque a pesar de la rotación, la generación de los factores no se altera.
Si tomamos la matriz de cargas \(\Lambda\) y la multiplicamos por una matriz ortogonal \(\omicron\), obtendríamos una matriz \(\Lambda_R\), la cual sería la matriz de cargas rotada en un ángulo determinado, tal como se muestra en la siguiente imagen:
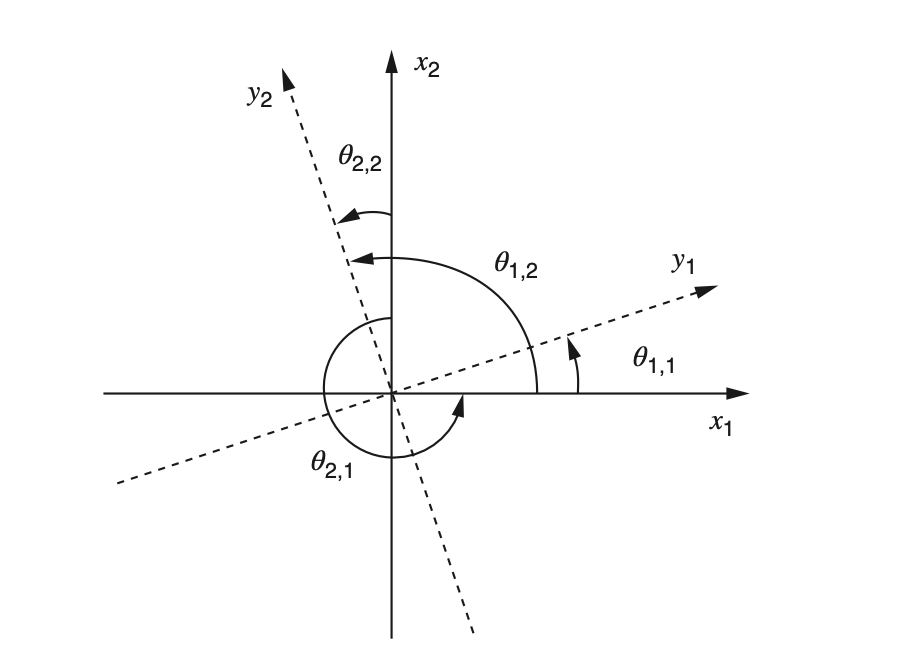
Rotación
Para obtener los nuevos planos \(y_1\), \(y_2\) la matriz \(\omicron\) por la que se multiplicó es \(\omicron_2\), que produce un movimiento en contra de las manecillas del reloj, si se quisiera rotar en el sentido horario, se multiplicaría por \(\omicron_1\)
Método de rotación VARIMAX y QUARTIMAX:
Existen numerosos métodos para rotar los factores, sin embargo, los más utilizados son varimax y quartimax, ya que ambos son rotaciones ortogonales, también existen rotaciones oblicuas, que no son tan usuales en la literatura.
Varimax:
El objetivo de la rotación varimax es maximizar la varianza dentro del factor, esto sucederá cunado haya mucha dispersión dentro de la matriz de cargas. En otras palabras, las cargas que son altas (cerca de |1.0|) o pequeñas (cerca de 0.0) en una matriz de correlación son preferibles a las cargas “mediocres”, ya que las cargas que se acercan a los límites superior e inferior de |1.0| y 0.0 sirven para maximizar la variabilidad, por esto, lo que hace el Varimax es dirigir las cargas grandes a ser aún mas grandes y las pequeñas a ser aún mas pequeñas, esto interrumpe el patrón de varianza mínima, haciendo los factores significativos e interpretables.
Para lograrse, los factores se deben multiplicar por la siguiente cantidad:
donde \(l_{ij}^2\) son las cargas al cuadrado en la posición \(i\) hasta \(p\) para cada factor, \(\overline{l^2_j}\) es el promedio de las cargas al cuadrado.
\(V\) generalmente se maximiza utilizando técnicas iterativas, por lo tanto, su maximización depende de un algoritmo informático por facilidad y eficiencia computacional.
Quartimax:
La rotación Quartimax se enfoca en las filas de la matriz de carga, buscando maximizar la varianza de las cargas a través de factores en lugar de dentro de los factores. Quartimax, está dado por:
Ahora la suma es a través de los factores \(j = 1\) a través de m. \(Q\) en este caso impulsa cargas a través de factores hacia 0 o |1| en una matriz de correlación en lugar de dentro de los factores.
Procedimiento para aplicar Análisis Factorial:
La metodología a seguirse puede resumirse en la siguiente figura:
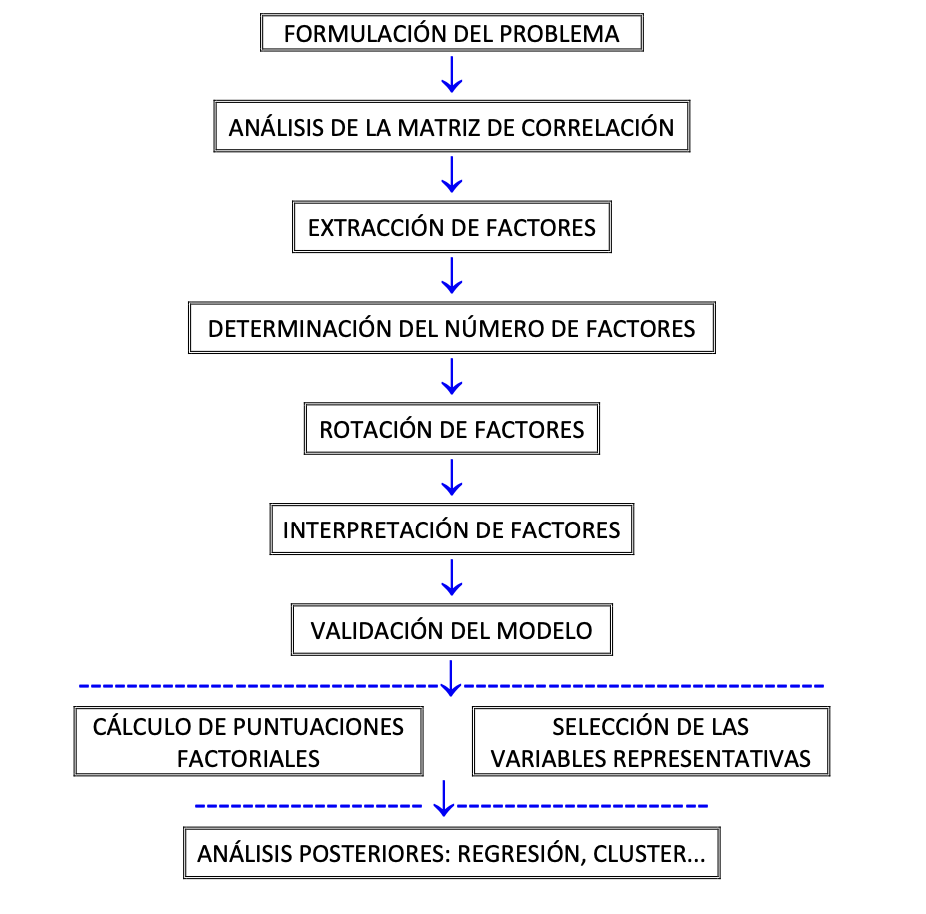
Procedimiento
Con la ayuda de cualquier paquete estadístico, es posible ajustar un modelo de Análisis Factorial exploratorio, para ello, se deben realizar algunas pruebas iniciales de correlación que permitirán asegurar que el modelo es aplicable a un conjunto de datos específico.
1. Análisis de la Matriz de correlación:
Como ya lo analizamos anteriormente, de la matriz de correlaciones, podemos identificar rápidamente si existen relaciones relevantes o no, con aquellas variables que cuenten con valores superiores a |0.2|. Sin embargo, no es del todo confiable porque en el modelo de Análisis Factorial, no estamos interesados en hacer inferencia sobre cada par de variables, sino por factores.
Si las correlaciones son bastante pequeñas por ejemplo inferiores a 0,10 a 0,20, es posible que no valga la pena realizar el análisis.
1.1. Bartlett Test:
Con el fin de evaluar si las magnitudes de las correlaciones son suficiente para el Análisis Factorial, se recomienda hacer una prueba de esfericidad de Bartlett, en la que se contrasta que la \(H_0\) responde a una matriz de correlaciones igual a la matriz identidad \(I\). Este test está dado por:
Donde \(p\) es el número de variables, \(n\) el de observaciones y \(ln|R|\) es el logaritmo del determinante de la matriz de correlaciones, y la expresión \(-(n-1) \frac{(2p+5)}{6}\) hará que permanezca constante tendiente a 6, y lo que hará variar será en función de \(|R|\).
Hipótesis:
1.2. Kaiser- Meyer- Olkin Test:
Este test es una relación entre la suma de las correlaciones al cuadrado y las correlaciones parciales al cuadrados Por lo general, se prefieren los valores superiores a 0,7–0,8, aunque siempre que los valores no sean demasiado bajos (por ejemplo; 0,6 o menos), por lo general no es motivo de preocupación. Esto es:
2. Extracción de comunalidades:
AL extraer las comunalidades tendremos una medida de cuánto tiene en común la variable observada dada, con los factores derivados, después de que la rutina del Análisis Factorial ha hecho su trabajo. Esto lo realiza cualquier paquete estadístico, ajustando una regresión para una variable \(X\), contra el resto del conjunto, y tomando sucesivamente todo el conjunto.
Conocer las comunalidades ayuda a definir la existencia sustantiva y la naturaleza de un factor, generalmente buscamos variables observadas que tengan correlaciones de magnitud relativamente alta con el factor dado. Nos podemos ayudar del Scree plot.
3. Determinación del número de factores:
Determinar el numero de factores puede ser complejo ya que en primer lugar se trata de cumplir con el criterio de parsimonia, pero, asu vez se pretende captar la mayor información posible, por ello podemos elegir el criterio para determinar el número de factores, desde un punto de vista teórico o hacia criterios mas robustos.
Criterios:
A priori
Regla Kaiser
Porcentaje de Varianza
Sedimentación (scree plot)
4.Interpretar los factores:
Para esto se identifican las variables cuyas correlaciones con el factor son mas elevada, en valor absoluto.
Se debe intentar dar un nombre a los factores.
Se puede hacer una representación gráfica de los factores con sus correlaciones.
Y se pueden eliminar aquellas cargas factoriales bajas para evitar información redundante.
5. Rotar la matriz:
Como ya lo vimos anteriormente, luego de extraer los factores, para convertir en un modelo interpretable y brindarle el máximo de variabilidad los factores, debe rotarse la matriz con alguno de los criterios explicados Varimax y Quartimax.
6. Calcular las puntuaciones factoriales:
Una vez calculados los factores rotados , se procede a calcular las matices de puntuaciones factoriales.
7. Validar el modelo:
Realizar pruebas de bondad de ajuste donde la \(H_0\) implica que la correlación observada entre las variables puede atribuirse a factores comunes es decir, que el número de factores son apropiados para explicar las varianzas originales.