Análisis Factorial

datos <- read.csv("EAM_2019.csv", sep = ";", dec = ",", header = T)
print(head(datos))

  ï..ciiu personal_mujer personal_hombre gasto_personal gasto_financiero
1    1051             36             140        9352991          3240559
2    1030             40             176        7334998          1468298
3    3290             15             172        6668544          1547666
4    3091             88             373       22088759         35203208
5    3290             18              53        5219070          2861773
6    3290             18              53        5219070          2861773
  costos_gastos_produccion gastos_adm_ventas inversion_AF    ventas
1                  6846304          22920307      4979745 192609248
2                  5941761          12310286      5615593 115741258
3                  6996020           2564695       773444  44580029
4                  4175751         171278876     10501572 162509864
5                 11037978          13691919      6423171  87324374
6                 11037978          13691919      6423171  87324374

Pruebas para el Análisis Factorial:

Matriz de correlaciones:

library("corrplot")

corrplot 0.92 loaded

corr <- cor(datos[,2:9])

corrplot(corr, method = "circle")
corrplot(corr, method = "number")
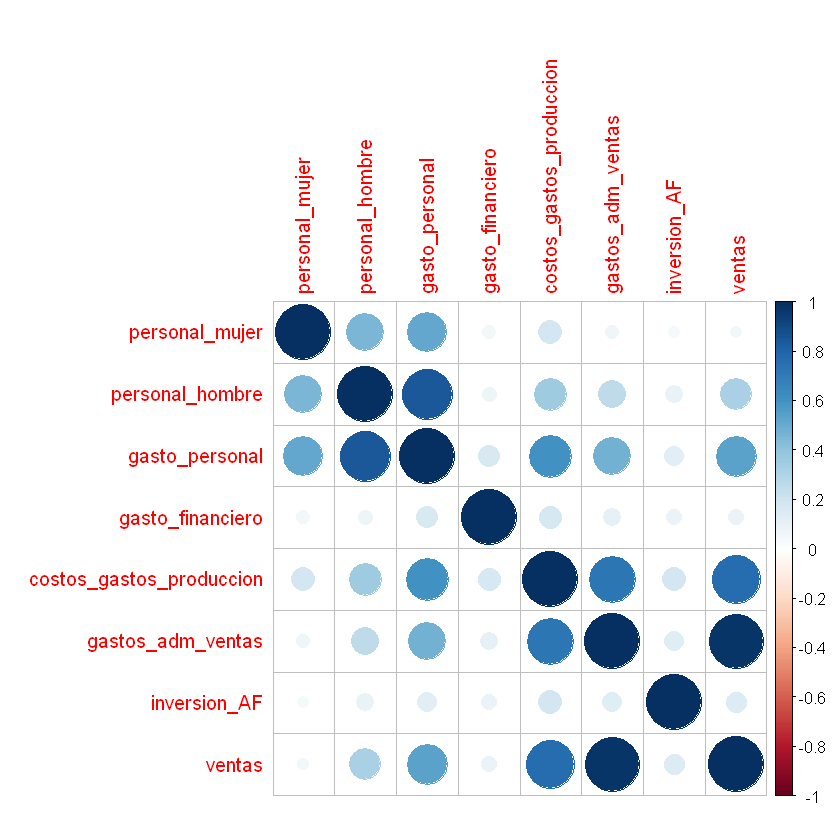
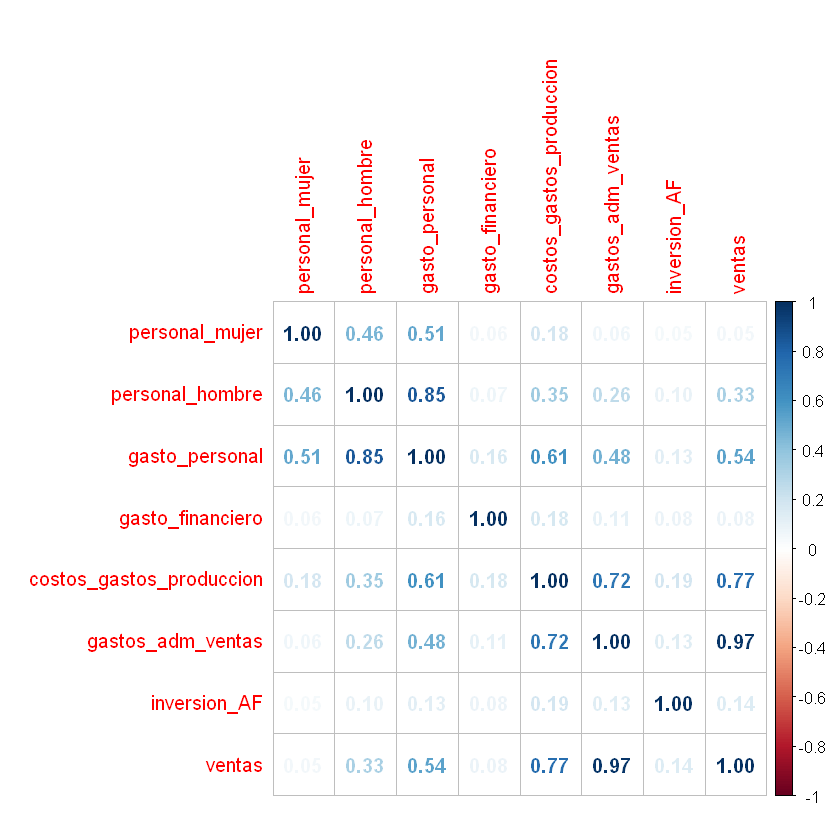
../../_images/output_6_0.png ../../_images/output_6_1.png

Determinante de la matriz de correlaciones:

Determinante cercano a cerco indica alta multicolinealidad. Esto significa que algunas variables son linealmente dependientes y una o más variables podrían ser expresadas como combinación lineal de otras variables y la técnica del Análisis Factorial es pertinente para analizar las variables.

det(corr)
0.00177061888189585

Test de Bartlett o test de esfericidad:

Se evalúa si la matriz de correlaciones es la identidad \(I\). Significa que las intercorrelaciones entre las variables son cero y el modelo de Análisis Factorial es inadecuado.

\[H_0: Corr = I\]
\[H_0: Corr \neq I\]

Se acepta la hipótesis nula si \(Valor-p > 0,05\)

bartlett.test(datos[,2:9])

    Bartlett test of homogeneity of variances

data:  datos[, 2:9]
Bartlett's K-squared = 29209, df = 7, p-value < 2.2e-16

Se rechaza la hipótesis nula porque \(Valor-p = 2,2e-16 < 0,05\), la matriz de correlaciones no es la Identidad. La aplicación del Análisis Factorial es adecuada. Esta afirmación también está soportada por el Determinante cercano a cero.

Kaiser-Meyer-Olkin - KMO:

Con esta prueba se busca si entre las variables hay factores comunes. Si las variables comparten factores comunes, el coeficiente de correlación parcial entre pares de variables es cercano a cero. Con los coeficientes de correlación parcial se mide el grado de relación lineal entre dos variables sin el efecto de las demás. Si se tienen coeficientes de correlación parcial altos, la aplicación del Análisis Factorial no es el adecuado.

Para comprobar lo anterior se calcula una Medida de Adecuación de la Muestra de KMO, \(0<=KMO<=1\).

\[KMO <0,6 --> Inaceptable\]
\[KMO >=0,6 --> Aceptable\]
\[KMO >=0,7 --> Bien\]

Con KMO cercano a cero indica que las correlaciones entre pares de variables no pueden ser explicadas por otras variables.

\[KMO = \frac{\sum_{j\neq i}\sum_{i\neq j}r^2_{ij}}{\sum_{j\neq i}\sum_{i\neq j}r^2_{ij}+\sum_{j\neq i}\sum_{i\neq j}r^2_{ij(p)}}\]

Donde,

\(r^2_{ij(p)}\): coeficiente de correlación parcial entre \((X_i, X_i)\).

Para esta prueba instalar el paquete: install.packages("psych")

library(psych)

KMO(datos[,2:9])

Kaiser-Meyer-Olkin factor adequacy
Call: KMO(r = datos[, 2:9])
Overall MSA =  0.67
MSA for each item =
          personal_mujer          personal_hombre           gasto_personal
                    0.63                     0.63                     0.67
        gasto_financiero costos_gastos_produccion        gastos_adm_ventas
                    0.47                     0.85                     0.64
            inversion_AF                   ventas
                    0.84                     0.63

Como \(KMO = 0,67\) es aceptable aplicar el Análisis Factorial porque sí hay presencia de factores comunes.

Determinación de la cantidad de factores:

1. Determinación “a priori”.

2. Regla de Kaiser: Eigenvalores mayores que 1,0.

3. Criterio del porcentaje de la varianza: varianza explicada por encima del 70%.

4. Criterio de Sedimentación: técnica del codo.

Regla de Kaiser y criterio de sedimentación:

plot(eigen(corr)$values, type = "b")
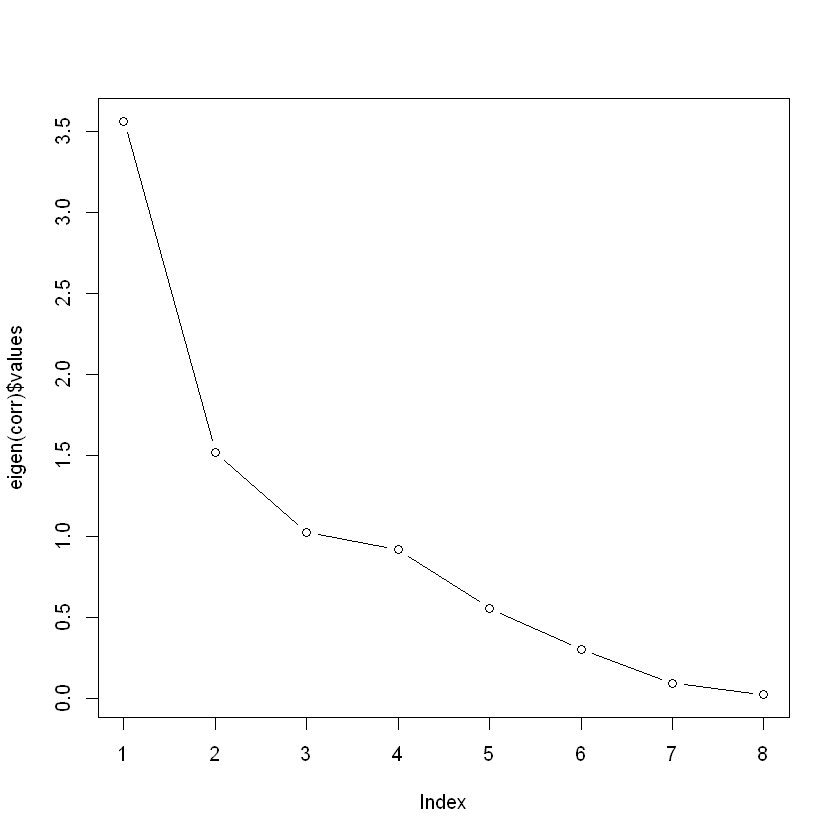
../../_images/output_23_0.png

Criterio del porcentaje de la varianza:

Se usará la función factanal() de la librería stats.

Se hará una prueba con 4 factores: factors = 4.

factanal(datos[,2:9], factors = 4)

Call:
factanal(x = datos[, 2:9], factors = 4)

Uniquenesses:
          personal_mujer          personal_hombre           gasto_personal
                   0.611                    0.209                    0.005
        gasto_financiero costos_gastos_produccion        gastos_adm_ventas
                   0.908                    0.166                    0.005
            inversion_AF                   ventas
                   0.958                    0.005

Loadings:
                         Factor1 Factor2 Factor3 Factor4
personal_mujer                    0.531           0.325
personal_hombre           0.150   0.869   0.118
gasto_personal            0.326   0.880   0.278   0.192
gasto_financiero                                  0.272
costos_gastos_produccion  0.593   0.218   0.593   0.289
gastos_adm_ventas         0.971   0.104   0.141   0.143
inversion_AF                              0.153
ventas                    0.939   0.173   0.289

               Factor1 Factor2 Factor3 Factor4
SS loadings      2.319   1.907   0.580   0.328
Proportion Var   0.290   0.238   0.072   0.041
Cumulative Var   0.290   0.528   0.601   0.642

Test of the hypothesis that 4 factors are sufficient.
The chi square statistic is 7.29 on 2 degrees of freedom.
The p-value is 0.0262

Extracción de factores:

  1. Método de Eje principal o Factor Principal.

  2. Máxima Verosimilitud.

En esta sesión se extraerán los factores por Máxima Verosimilitud. La función factanal() solo extraer los factores por este método. Para aplicar los otros métodos se recomienda usar la función fa() de la librería psych, con el argumento fm = "pa" para el método de Eje principal o Factor Principal.

Por ejemplo: fa(datos[,2:9], nfactors = 4, rotate = "none", fm = "pa")

Rotación de los factores:

La función factanal() por defecto rota los factores por Varimax, pero se puede cambiar el método de rotación con el argumento:

rotation =: "varimax", "quartimax", "equamax". Estos métodos son rotaciones ortogonales.

Para algunos métodos de rotación instalar la librería install.packages("GPArotation")

library(GPArotation)

fit <- factanal(datos[,2:9], factors = 3, rotation = "varimax")
fit

Call:
factanal(x = datos[, 2:9], factors = 3, rotation = "varimax")

Uniquenesses:
          personal_mujer          personal_hombre           gasto_personal
                   0.660                    0.162                    0.005
        gasto_financiero costos_gastos_produccion        gastos_adm_ventas
                   0.902                    0.296                    0.048
            inversion_AF                   ventas
                   0.971                    0.005

Loadings:
                         Factor1 Factor2 Factor3
personal_mujer                    0.527   0.247
personal_hombre           0.203   0.892
gasto_personal            0.408   0.869   0.271
gasto_financiero                          0.299
costos_gastos_produccion  0.722   0.249   0.349
gastos_adm_ventas         0.971
inversion_AF              0.131
ventas                    0.986   0.141

               Factor1 Factor2 Factor3
SS loadings      2.666   1.923   0.362
Proportion Var   0.333   0.240   0.045
Cumulative Var   0.333   0.574   0.619

Test of the hypothesis that 3 factors are sufficient.
The chi square statistic is 50.96 on 7 degrees of freedom.
The p-value is 9.38e-09

Uniquenesses - \(\Psi\): Unicidad: proporción de la varianza no explicada.

print(fit$uniquenesses)

  personal_mujer          personal_hombre           gasto_personal
      0.66023136               0.16158472               0.00500000
gasto_financiero costos_gastos_produccion        gastos_adm_ventas
      0.90243324               0.29566162               0.04824951
    inversion_AF                   ventas
      0.97090998               0.00500000

Comunalidad - \(\Lambda\): \(1-\Psi\). Proporción de la varianza que sí se puede explicar por cada variable. También son suma de las cargas al cuadrado por cada variable.

print(apply(fit$loadings^2, 1, sum))

  personal_mujer          personal_hombre           gasto_personal
      0.33971591               0.83841043               0.99500077
gasto_financiero costos_gastos_produccion        gastos_adm_ventas
      0.09756084               0.70433543               0.95175045
    inversion_AF                   ventas
      0.02914470               0.99505497

``SS loadings:`` suma de las cargas al cuadrado por cada factor. La regla de Kaiser dice que cada factor debe tener un valor mayor a 1.

Valor p: \(H_0\) es que los factores seleccionados son los adecuados. Se acepta si valor p > 0,05. Se rechaza si valor p es pequeño (< 0,05).

Cálculo de las puntuaciones o cargas factoriales:

  1. Método de Regresión.

  2. Método de Barlett.

Se agrega el argumento:

scores =: "regression" o "Bartlett". Por defecto hace el cálculo con scores = "regression"

fit <- factanal(datos[,2:9], factors = 3, rotation = "varimax", scores = "regression")
fit

Call:
factanal(x = datos[, 2:9], factors = 3, scores = "regression",     rotation = "varimax")

Uniquenesses:
          personal_mujer          personal_hombre           gasto_personal
                   0.660                    0.162                    0.005
        gasto_financiero costos_gastos_produccion        gastos_adm_ventas
                   0.902                    0.296                    0.048
            inversion_AF                   ventas
                   0.971                    0.005

Loadings:
                         Factor1 Factor2 Factor3
personal_mujer                    0.527   0.247
personal_hombre           0.203   0.892
gasto_personal            0.408   0.869   0.271
gasto_financiero                          0.299
costos_gastos_produccion  0.722   0.249   0.349
gastos_adm_ventas         0.971
inversion_AF              0.131
ventas                    0.986   0.141

               Factor1 Factor2 Factor3
SS loadings      2.666   1.923   0.362
Proportion Var   0.333   0.240   0.045
Cumulative Var   0.333   0.574   0.619

Test of the hypothesis that 3 factors are sufficient.
The chi square statistic is 50.96 on 7 degrees of freedom.
The p-value is 9.38e-09

Realizar el Análisis Factorial con más factores y otros métodos de rotación.