Repaso Álgebra Lineal

Determinantes:

Matrices $2x2$:

El área del plano se llama Determinante.

\[\begin{split}Plano = \begin{bmatrix} 4 & 0 \\ 0 & 4 \end{bmatrix}, Determinante = 16\end{split}\]

El área es igual a $4\times4=16$. Para matrices de orden 2 $(2x2)$ el Determinante se calcula multiplicando los valores de la diagonal principal y restando la multiplicación de la diagonal secundaria.

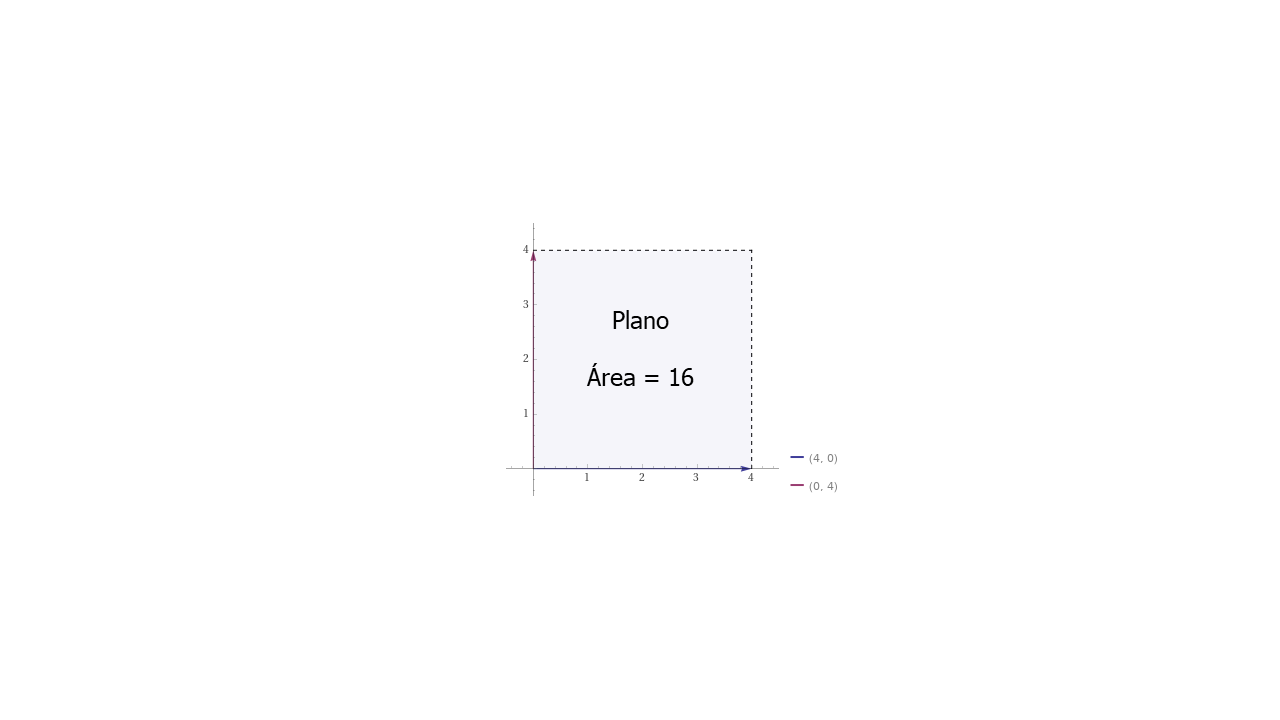
Plano

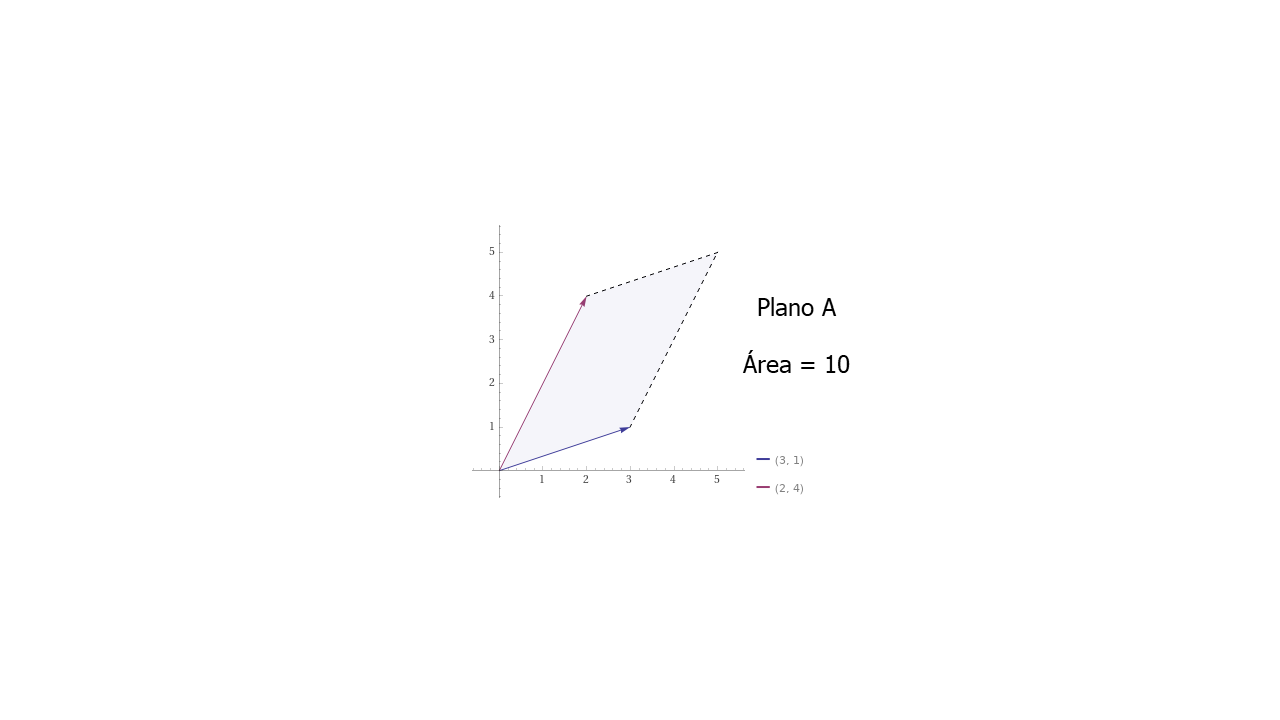
PlanoA

Siendo $A = \begin{bmatrix} a & b \\ c & d \end{bmatrix}$

\[\begin{split}det(A) = det\begin{bmatrix} a & b \\ c & d \end{bmatrix} = a\times d - b\times c\end{split}\]

\[\begin{split}det(A) = det\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} = 3\times 4 - 2\times 1 = 10\end{split}\]

En ocasiones vemos que el Determinante se expresa en valor absoluto así $det(A) = |A|$, pero también se puede expresar con el signo negativo. Esto ocurre si cambiamos el orden de los vectores.

Determinante2x2

\[\begin{split}B = \begin{bmatrix} 2 & 2 \\ 1 & 3 \end{bmatrix}, Determinante = 4\end{split}\]

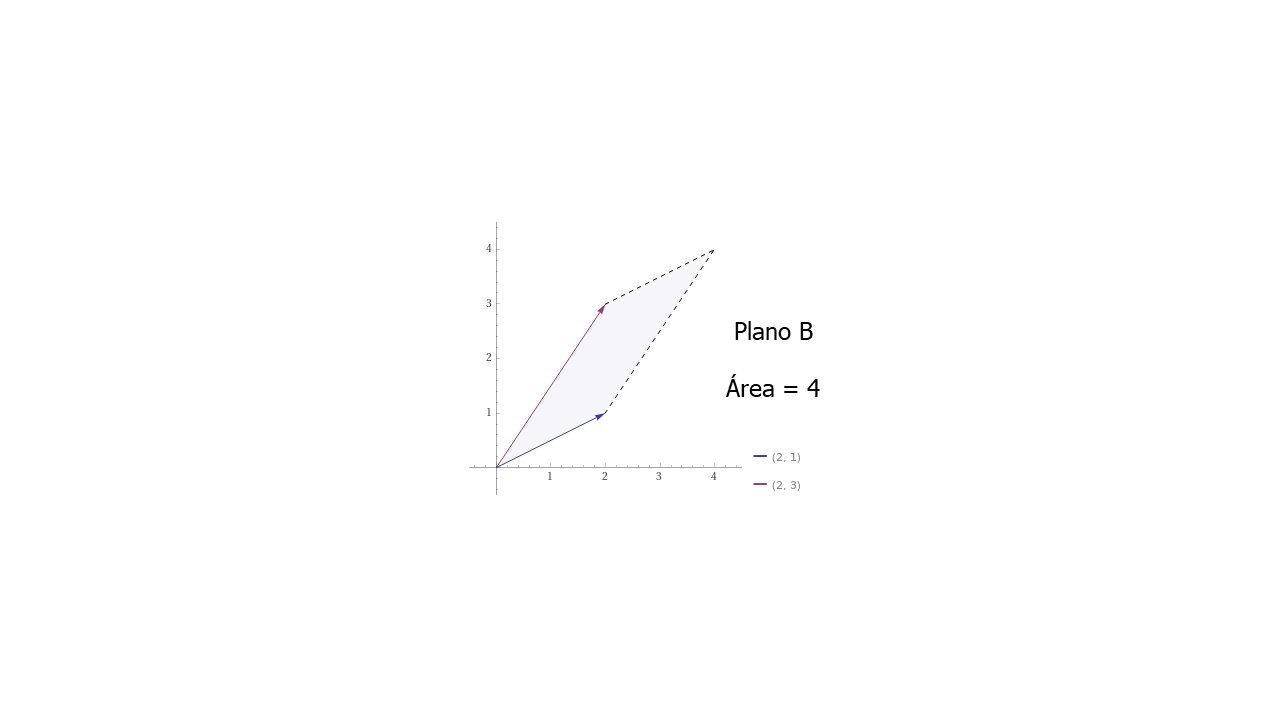
PlanoB

\[\begin{split}C = \begin{bmatrix} 1,2 & 2 \\ 1 & 1,2 \end{bmatrix}, Determinante = 0,64\end{split}\]

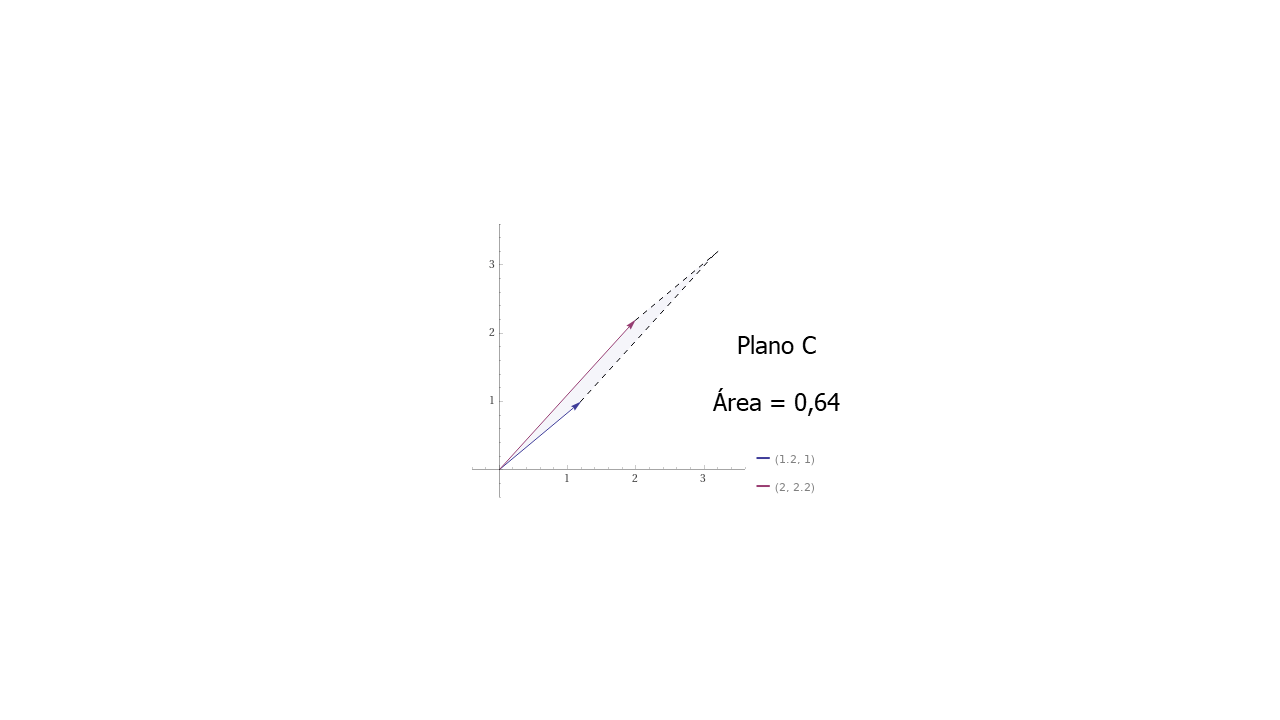
PlanoC

\[\begin{split}A = \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}, Determinante = 10\end{split}\]

\[\begin{split}B = \begin{bmatrix} 2 & 2 \\ 1 & 3 \end{bmatrix}, Determinante = 4\end{split}\]

\[\begin{split}C = \begin{bmatrix} 1,2 & 2 \\ 1 & 1,2 \end{bmatrix}, Determinante = 0,64\end{split}\]

Note que en los ejemplos de las matrices $A$, $B$ y $C$ los valores de la diagonal principal disminuyen y se obtiene un Determinante menor. Es fácil intuir que un Determinante más pequeño, por ejemplo, igual a cero, el resultado es un solo vector. Este vector, más adelante se llamará Autovector.

Matrices $3x3$:

Para matrices $3\times3$ el Determinante (volumen, no área) es:

Siendo $A = \begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i\end{bmatrix}$

\[\begin{split}det(A) = det\begin{bmatrix} a & b & c \\ d & e & f \\ g & h & i\end{bmatrix}= a\begin{bmatrix} e & f \\ h & i\end{bmatrix}-b\begin{bmatrix} d & f \\ g & i\end{bmatrix}-c\begin{bmatrix} d & e \\ g & h \end{bmatrix}\end{split}\]

Transformaciones lineales:

Una matriz podría verse como una transformación lineal porque transforman linealmente los vectores unitarios ($\hat{i}$, $\hat{j}$).

Los vectores unitarios conforman el siguiente plano:

\[\begin{split}\begin{bmatrix} 1 & 0 \\ 0 & 1 \end{bmatrix}\end{split}\]

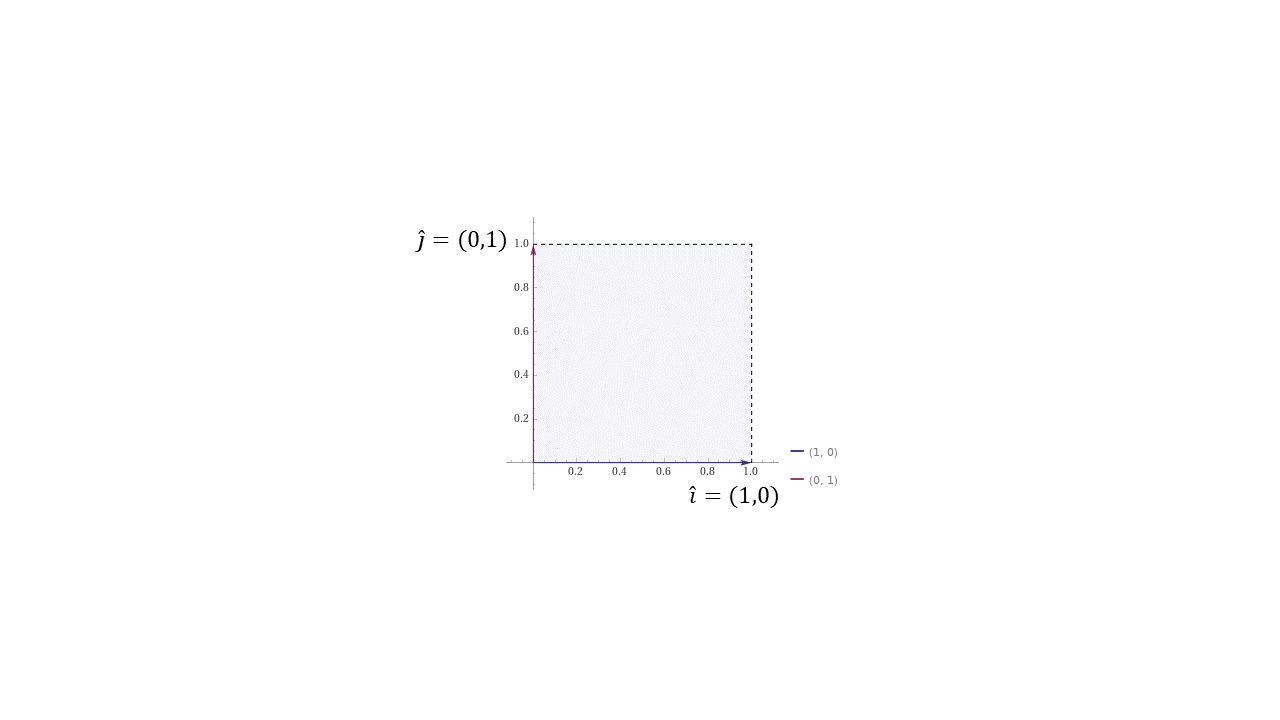
VectoresUnitarios

Siendo $A =\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}$, la transformación lineal de los dos vectores unitarios es la siguiente:

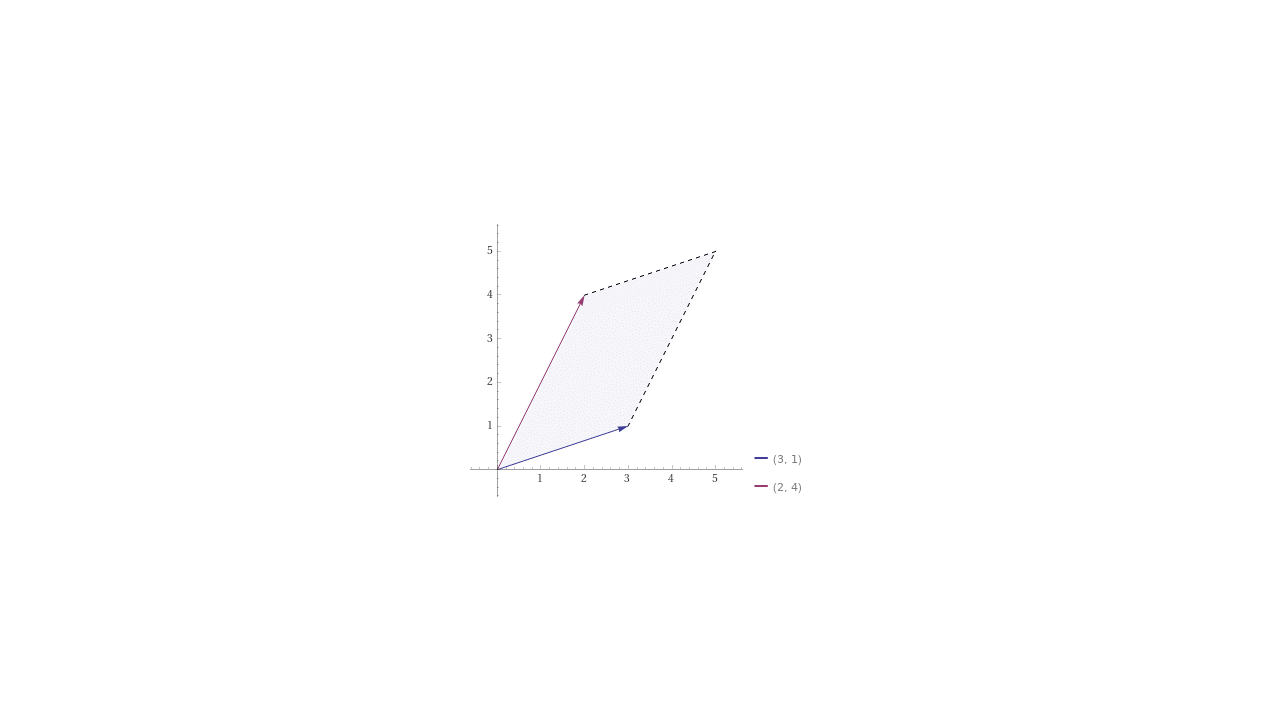
TransformaciónLineal

Analicemos la transformación que realizó la matriz $A$ a tres vectores del plano de vectores unitarios:

El vector $\begin{bmatrix} 1 \\ 0 \end{bmatrix}$ se transformó en el vector $\begin{bmatrix} 3 \\ 1 \end{bmatrix}$. El vector nuevo tiene una dirección diferente que el inicial.
El vector $\begin{bmatrix} 0 \\ 1 \end{bmatrix}$ se transformó en el vector $\begin{bmatrix} 2 \\ 4 \end{bmatrix}$. El vector nuevo tiene una dirección diferente que el inicial.
El vector $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ se transformó en el vector $\begin{bmatrix} 5 \\ 5 \end{bmatrix}$. El vector nuevo sí conservó la dirección, pero tiene una magnitud diferente (es un vector escalado).

Al hacer la transformación lineal de $A$, el vector transformado $\begin{bmatrix} 5 \\ 5 \end{bmatrix}$ es el mismo vector $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$, pero con una magnitud de 5, es decir: $\begin{bmatrix} 5 \\ 5 \end{bmatrix} = 5\begin{bmatrix} 1 \\ 1 \end{bmatrix}$. Así que el vector $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$ se llama Autovector o Eigenvector de la matriz $A$ y el escalar 5 se llama Autovalor o Eigenvalor de la matriz $A$.

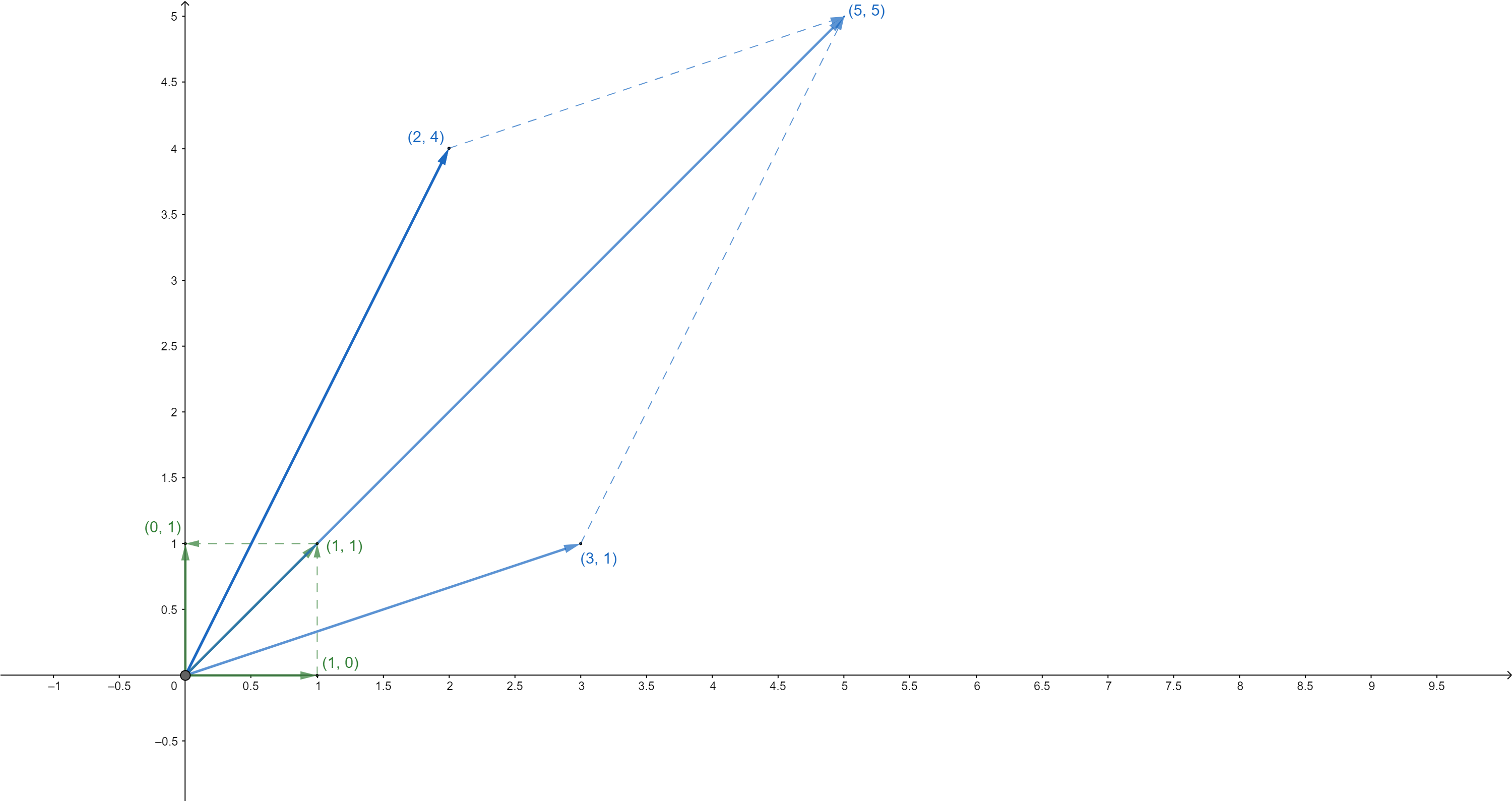
TransformaciónLineal.

Autovalores y Autovectores:

Con lo anterior podemos concluir que un Autovector :math:`(x)` es aquel que es transformado por una matriz y conserva su dirección, pero puede aumentar o disminuir de magnitud en $\lambda$ veces. Por tanto, el escalar $\lambda$ es un Autovalor. Lo anterior cumple la siguiente ecuación:

\[Ax = \lambda x\]

Donde,

$A$: es una matriz del orden $nxn$.

$x$: es el Autovector o Eigenvector de $A$.

$\lambda$: es el Autovalor o Eigenvalor de $A$. Es un escalar.

Para el ejemplo:

\[\begin{split}\begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix} \begin{bmatrix} 1 \\ 1 \end{bmatrix} = 5 \begin{bmatrix} 1 \\ 1 \end{bmatrix}\end{split}\]

Para hallar $x$ y $\lambda$ matemáticamente se hace lo siguiente:

\[(A - \lambda I)x = 0\]

$I$: es la matriz identidad.

\[\begin{split}(A - \lambda I) = \begin{bmatrix} a -\lambda & b \\ c & d-\lambda \end{bmatrix}\end{split}\]

$det(A - \lambda I)=0$ es llamada ecuación característica.

Anteriormente, gráficamente habíamos restado solo los valores de la diagonal principal de la matriz $A = \begin{bmatrix} 3 & 2 \\ 1 & 4 \end{bmatrix}$, se había concluido que el Determinante se volvía cero y el vector resultante era $\begin{bmatrix} 1 \\ 1 \end{bmatrix}$. Este vector es el Autovector de la matriz $A$.

Entonces, $\lambda$ es Autovalor de $A$ si y solo si: $det(A - \lambda I)) = 0$

Para una matriz del orden $nxn$ tendremos $n$ Autovectores y $n$ Autovalores. En el ejemplo anterior se mencionó un Autovector y un Autovalor, pero la solución completa es la siguiente:

\[\begin{split}(A - \lambda I) = \begin{bmatrix} 3 -\lambda & 2 \\ 1 & 4-\lambda \end{bmatrix}\end{split}\]

\[det(A - \lambda I)) = 0\]

\[(3-\lambda)(4-\lambda)-2 = 0\]

\[\lambda^2-7\lambda+10=0\]

\[\lambda_1 = 2, \lambda_2 = 5\]

Para estos dos Autovalores, los dos Autovectores son:

Para $\lambda_1 = 2$, $ x_1=

$

Para $\lambda_2 = 5$, $ x_2=

$

Los dos Autovectores son ortogonales, tienen un ángulo de 90°.

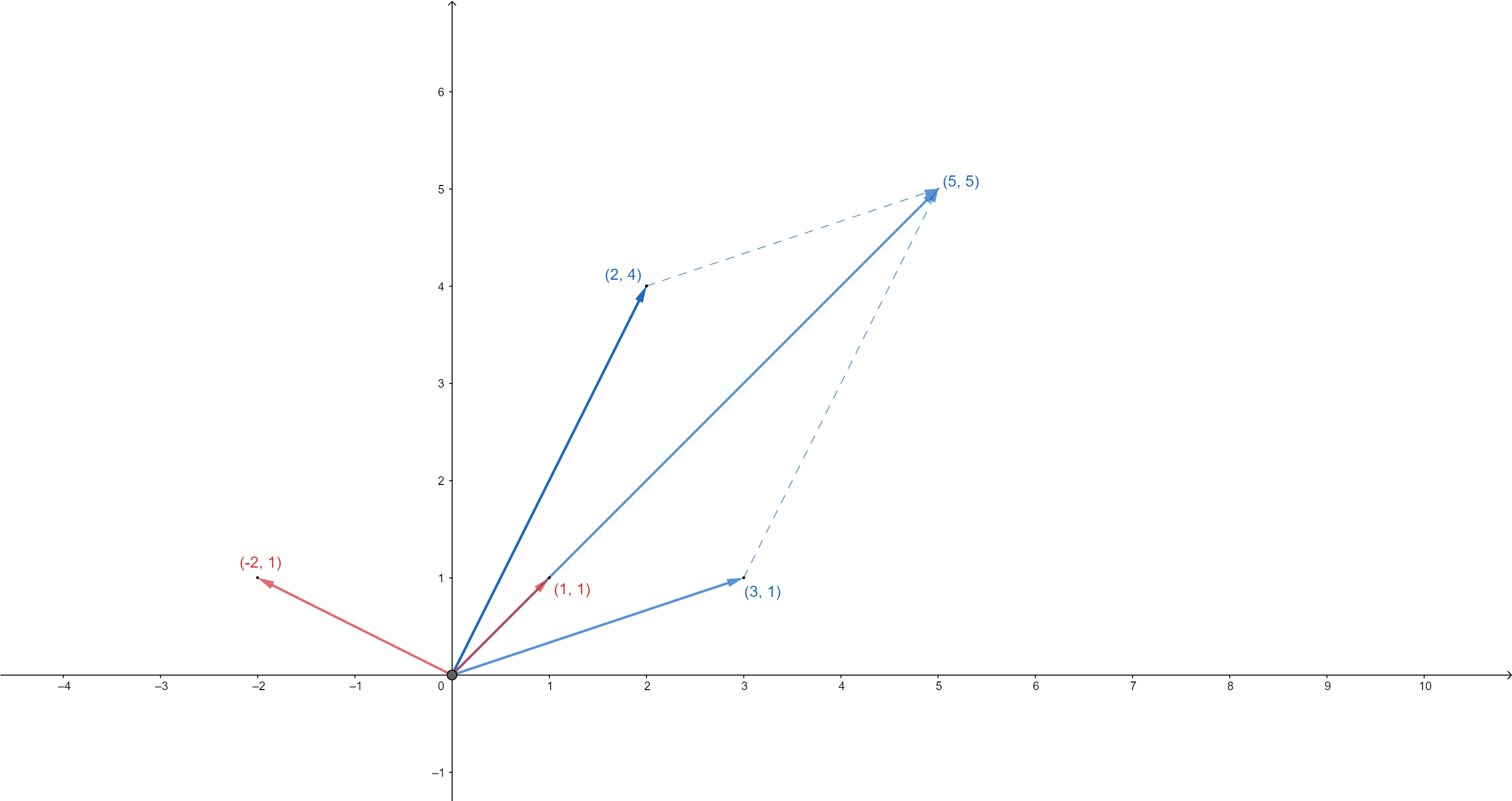
Autovectores