Ejemplo de ACP en R
datos <- read.csv("EAM_2019.csv", sep = ";", dec = ",", header = T)
print(head(datos))
ï..ciiu personal_mujer personal_hombre gasto_personal gasto_financiero
1 1051 36 140 9352991 3240559
2 1030 40 176 7334998 1468298
3 3290 15 172 6668544 1547666
4 3091 88 373 22088759 35203208
5 3290 18 53 5219070 2861773
6 3290 18 53 5219070 2861773
costos_gastos_produccion gastos_adm_ventas inversion_AF ventas
1 6846304 22920307 4979745 192609248
2 5941761 12310286 5615593 115741258
3 6996020 2564695 773444 44580029
4 4175751 171278876 10501572 162509864
5 11037978 13691919 6423171 87324374
6 11037978 13691919 6423171 87324374
datos <- datos[, 2:9]
print(head(datos))
personal_mujer personal_hombre gasto_personal gasto_financiero
1 36 140 9352991 3240559
2 40 176 7334998 1468298
3 15 172 6668544 1547666
4 88 373 22088759 35203208
5 18 53 5219070 2861773
6 18 53 5219070 2861773
costos_gastos_produccion gastos_adm_ventas inversion_AF ventas
1 6846304 22920307 4979745 192609248
2 5941761 12310286 5615593 115741258
3 6996020 2564695 773444 44580029
4 4175751 171278876 10501572 162509864
5 11037978 13691919 6423171 87324374
6 11037978 13691919 6423171 87324374
ACP:
acp <- prcomp(datos, center = T, scale. = T)
print(summary(acp))
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 1.8881 1.2332 1.0115 0.9572 0.74549 0.5514 0.30452
Proportion of Variance 0.4456 0.1901 0.1279 0.1145 0.06947 0.0380 0.01159
Cumulative Proportion 0.4456 0.6357 0.7636 0.8782 0.94763 0.9856 0.99722
PC8
Standard deviation 0.14911
Proportion of Variance 0.00278
Cumulative Proportion 1.00000
Se obtienen ocho (\(p = 8\)) Componentes Principales. Cada uno explica un porcentaje de la variación total en el conjunto de datos.
PC1 explica el 44,56% de la varianza total, esto significa que casi la mitad de la información del conjunto de datos que contiene ocho variable puede encapsularse en solo este Componente Principal.
PC2 explica el 19,01% de la varianza total. Entonces, al resumir la información en los primeros dos Componentes Principales se puede explicar el 63,57% de la varianza.
acp
Standard deviations (1, .., p=8):
[1] 1.8881364 1.2332124 1.0114793 0.9572381 0.7454911 0.5513719 0.3045164
[8] 0.1491134
Rotation (n x k) = (8 x 8):
PC1 PC2 PC3 PC4
personal_mujer 0.2106928 0.57578375 -0.02214712 0.02361349
personal_hombre 0.3585481 0.46745657 -0.08352398 0.04828165
gasto_personal 0.4548743 0.32937778 -0.04737869 -0.02403973
gasto_financiero 0.1115576 0.01348448 0.74003083 -0.65388863
costos_gastos_produccion 0.4461470 -0.21007377 0.01448462 -0.02746956
gastos_adm_ventas 0.4336228 -0.39544860 -0.11741035 -0.03425391
inversion_AF 0.1238028 -0.05636775 0.64060409 0.75295144
ventas 0.4530927 -0.37094199 -0.13518240 -0.00996259
PC5 PC6 PC7 PC8
personal_mujer -0.772202925 0.11726775 -0.09769967 0.0586448480
personal_hombre 0.542176918 0.14380998 -0.57271625 -0.0312928834
gasto_personal 0.253374106 -0.09286009 0.77820633 -0.0578830139
gasto_financiero 0.021041260 0.09724572 -0.03932248 0.0266717602
costos_gastos_produccion -0.136769241 -0.82513357 -0.23007970 -0.0580479890
gastos_adm_ventas -0.155556129 0.41861887 -0.04299362 -0.6628311912
inversion_AF 0.003127729 0.06144540 0.01999398 -0.0009877992
ventas -0.046822464 0.29601441 -0.01070724 0.7408130522
La matriz de rotación muestra las cargas que cada Componente Principal le otorga a cada variable original, por ejemplo, en el PC1, la variable de mayor peso es Gasto de personal porque tiene la carga más alta, la siguiente en importancia es Ventas.
names(acp)
- 'sdev'
- 'rotation'
- 'center'
- 'scale'
- 'x'
Objeto |
Descripción |
|---|---|
|
Desviación estándar de cada Componente
Principal. Los Eigenvalores son
|
|
Matriz con las cargas por cada variable y Componente Principal. Las columnas son los Eigenvectores. |
|
Promedio de cada variable original |
|
Desviación estándar de cada variable original |
|
Proyección de cada variable sobre las Componentes Principales |
Número de Componentes Principales:
Para tomar la decisión de cuántos Componentes Principales emplear y reducir la dimensión se aplica la técnica del codo con el Scree plot.
Los Eigenvalores se grafican en orden descendente en magnitud. En el eje
\(x\) están los Componentes Principales en el mismo orden que
aparecen en summary() y en el eje \(y\) la varianza asociada
\(\lambda\).
Scree plot:
En este gráfico se muestra la varianza que logra capturar cada Componente Principal en orden de importancia.
screeplot(acp, main = "Screeplot", col = "blue", type = "lines", pch = 19)

Biplot:
El Biplot es una comparación de las cargas de las variables en las primera Componentes Principales.
biplot(acp, scale = 0)
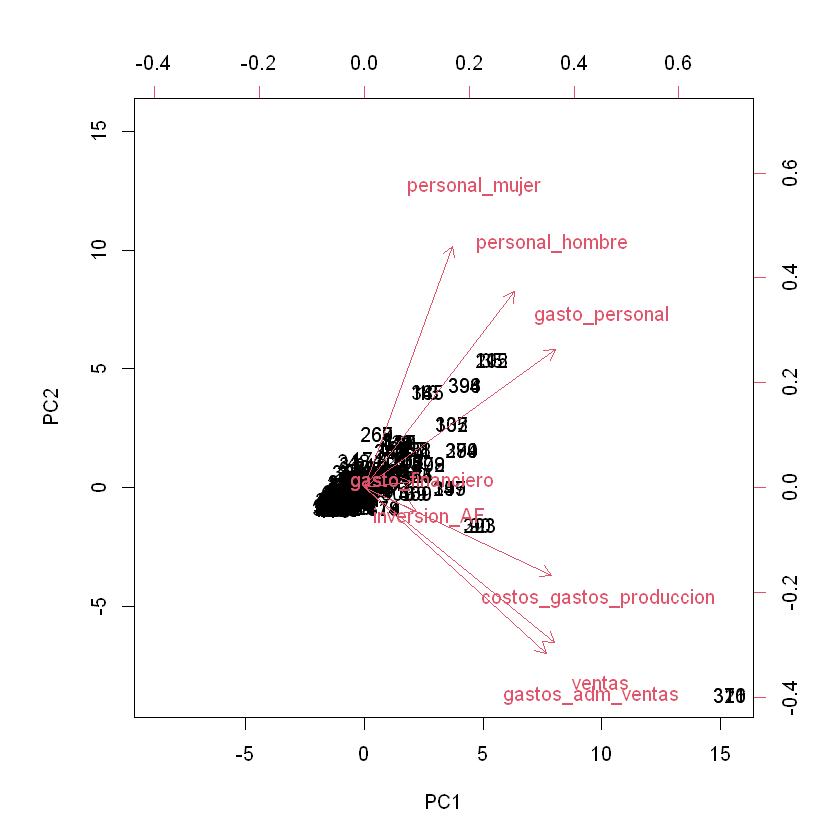
Las variables con mayores cargas en PC1 son las siguientes ordenadas de mayor a menor:
Gasto personal.
Ventas.
Costos y gastos de producción.
Gastos en administración y ventas.
En el Biplot estas cuatro variables se muestran con las de mayor desplazamiento en el eje \(x\), PC1.
Las dos variables con las cargas más bajas en PC1 son Gasto financiero e Inversión en AF. En el Biplot se muestran como las de menor desplazamiento horizontal. Son las más cercanas al centro.
Para PC2 se deben observar los desplazamientos verticales. La variable con mayor carga en valor absoluto es Personal mujer, seguido de Personal hombre y de tercera Gastos en administración y ventas, esta última variable con una carga negativa, por eso el desplazamiento es hacia abajo.
Los vectores más cercanos entre sí indican alta correlación. Así que Ventas y Gastos en administración y ventas están muy correlacionadas.
PC1 está positivamente correlacionado con todas las variables.
PC2 está positivamente correlacionado con Personal mujer, Personal hombre, Gasto personal y Gasto financiero. Además, está negativamente correlacionado con Inversión en AF, Costos y gastos de producción y Gastos en administración y ventas.
Lo anterior también se puede analizar con la matriz de rotación.
Conclusión:
Por el criterio del codo escogemos las primeras tres Componentes Principales. Así se resumen las ocho variables en tres dimensiones, las cuales resumen el 76,36% de la varianza total.
Las tres variables son la multiplicación de cada carga por las variables del conjunto de datos.
PC1 <- apply(acp$rotation[, 1]*datos, 1, sum)
PC2 <- apply(acp$rotation[, 2]*datos, 1, sum)
PC3 <- apply(acp$rotation[, 3]*datos, 1, sum)
PC <- cbind(PC1, PC2, PC3)
head(PC)
| PC1 | PC2 | PC3 |
|---|---|---|
| 102065975 | -33763325 | 2699749 |
| 62936669 | -42387137 | -16784958 |
| 12595763 | 2010874 | 30508600 |
| 171289275 | -136378975 | -22673169 |
| 32005092 | 55046810 | -1972086 |
| 47079967 | 39589641 | -11339209 |