Práctica 6: Análisis y selección de portafolios

Obtención del portafolio eficiente o de mínima varianza

Una vez obtenida la frontera eficiente, tal como se realizó en Optimización de portafolios, es posible determinar cuales son los pesos óptimos, a partir del portafolio de mínima varianza (punto más a la izquierda de la frontera eficiente). Para ello, se cra un objeto de clase fPortfolio llamado Portafolio_Efi, que contendrá la salida de la función efficientPortfolio(), a la cual se le ingresa los siguientes argumentos: * El objeto al que se le aplicará el modelo para determinar el portafolio eficiente, que en este caso serían los rendimientos como una serie de tiempo. por ello, se hace uso de la función as.timeSeries() sobre Rdtos[-1,]. * El argumento con el que se configura la optimización spec = que va a ser igual a las escificaciones que se ajustaron antes de crear la frontera eficiente y que se llamó espcartera. * la restricción de no negatividad que también se determinó antes de configurar la frontera como la variable constraints, donde se indicaba se permiten posciones en largo,pero no ventas en corto "LongOnly".

Estqa función permite visualizar los argumentos del modelo Title: los pesos Portfolio Weights:, el riesgo estimado Covariance Risk Budgets: y los retornos esperados Target Returns and Risks:.

Para obtener únicamente los pesos del portafolio eficiente,se utiliza la función getWeights() sobre el objeto Portafolio_Efi, y así se obterndrá el vector de los pesos para el portafolio de mínima varianza. En este caso se debe invertir un 31.43% en BABA, un 0% en APPL un 66.69% en WMT un 0% en WBA, un 1.88% en TSLA y 0% en PEP.

Portafolio_Efi= efficientPortfolio(as.timeSeries(Rdtos[-1,]),spec = espcartera,constraints)
Portafolio_Efi
W_efi=getWeights(Portafolio_Efi)
W_efi

Title:
 MV Efficient Portfolio
 Estimator:         covEstimator
 Solver:            solveRquadprog
 Optimize:          minRisk
 Constraints:

Portfolio Weights:
  BABA   AAPL    WMT    WBA   TSLA    PEP
0.3143 0.0000 0.6669 0.0000 0.0188 0.0000

Covariance Risk Budgets:
  BABA   AAPL    WMT    WBA   TSLA    PEP
0.3143 0.0000 0.6669 0.0000 0.0188 0.0000

Target Returns and Risks:
  mean    Cov   CVaR    VaR
0.0006 0.0148 0.0343 0.0174

Description:
 Wed Apr 01 19:18:37 2020 by user: Natalia
BABA
0.314314558226735
AAPL
0
WMT
0.666878313798239
WBA
0
TSLA
0.0188071279750264
PEP
0

Portafolio tangente a la Línea del Mercado de Capitales

Este portafolio tangente (punto rojo en la forntera eficiente) se determina de forma similar al anterior, por medio de la función tangencyPortfolio() y los mismos argumentos mencionados.

Para conocer los pesos del portafolio tangente, se aplica la misma función getWeights(), pero esta vez, sobre el objeto Portafolio_tang, y se obtendrá el vector de pesos.

Portafolio_tang = tangencyPortfolio(as.timeSeries(Rdtos[-1,]),spec = espcartera,constraints)
Portafolio_tang
W_tang=getWeights(Portafolio_tang)
W_tang

Title:
 MV Tangency Portfolio
 Estimator:         covEstimator
 Solver:            solveRquadprog
 Optimize:          minRisk
 Constraints:

Portfolio Weights:
  BABA   AAPL    WMT    WBA   TSLA    PEP
0.0000 0.7407 0.1135 0.0000 0.1458 0.0000

Covariance Risk Budgets:
  BABA   AAPL    WMT    WBA   TSLA    PEP
0.0000 0.7599 0.0486 0.0000 0.1915 0.0000

Target Returns and Risks:
  mean    Cov   CVaR    VaR
0.0014 0.0221 0.0587 0.0334

Description:
 Wed Apr 01 19:18:37 2020 by user: Natalia
BABA
0
AAPL
0.740694129080433
WMT
0.113543867783967
WBA
0
TSLA
0.145762003135599
PEP
0

Ratio de Sharpe para portafolios

El Ratio de Sharpe que permite medir el premio por el riego asumido al invertir en un instrumento no seguro. Por tanto el portafolio con mayor ratio será preferido por el inversionista.

El ratio de Sharpe se determina por medio de la fórmula:

\[Sharpe= \frac{(R_p-R_f)}{\sigma}\]

Para ello se requiere extraer el rendimiento de cada uno de los portafolios (eficiente y tangente), por merdio de la función getTargetReturn() y los riesgos (\(\sigma\)), con la función getTargetRisk(), de esta forma, se obtiene vectores que contienen la media de los rendimientos mu y el vector de riesgos de donde se extrae sigma que se encuentra en la posición 2 del vector Riskport_efi[2]. Ya con estos datos, se procede a calcular la fórmula anterior.

#Ratio Sharpe portafolio eficiente:
Rport_efi=getTargetReturn(Portafolio_Efi)
Rport_efi
Riskport_efi= getTargetRisk(Portafolio_Efi)
Riskport_efi
sigma_efi=Riskport_efi[2]
sigma_efi
Sharpe_efi=(Rport_efi[2]-rf)/sigma_efi
Sharpe_efi
mean
0.00059411834022739
mu
0.00059411834022739
Cov
0.014768226056284
Sigma
0.014768226056284
CVaR
0.0342943590049817
VaR
0.0174098349373304
Sigma: 0.014768226056284mu: 0.0382658240789136

De forma similar se realiza el realiza el Ratio de Sharpe para el portafolio tangente:

Rport_tang=getTargetReturn(Portafolio_tang)
Rport_tang
Riskport_tang= getTargetRisk(Portafolio_tang)
Riskport_tang
sigma_tang=Riskport_tang[2]
sigma_tang
Sharpe_tang=(Rport_tang[2]-rf)/sigma_tang
Sharpe_tang
mean
0.00142297402065197
mu
0.00142297402065197
Cov
0.0220625645106896
Sigma
0.0220625645106896
CVaR
0.0587050975805006
VaR
0.0334424983815035
Sigma: 0.0220625645106896mu: 0.0631827736968916

Gráficos de Torta para visualizar los pesos de los portafolios

Una forma sencilla de visulaizar los pesos en los que se va a repartir el recurso, es realizando un gráfico cilcular o comunmente llamado gráfico de torta. la función que se utiliza es weightsPie(), sobre el objeto Portafolio_Efi y con argumentos de configuración del gráfico como color col= y tamaño de la torta radius=. con la función mtext(), se configura el título del gráfico, que se encentra arriba a la izquierda.

#torta portafolio eficiente
win.graph(15,13)
weightsPie(Portafolio_Efi, col= col, radius = 0.5)
mtext(text = "portafolio eficiente", side = 3, line = 1.5, font = 1, cex = 0.7, adj = 0)
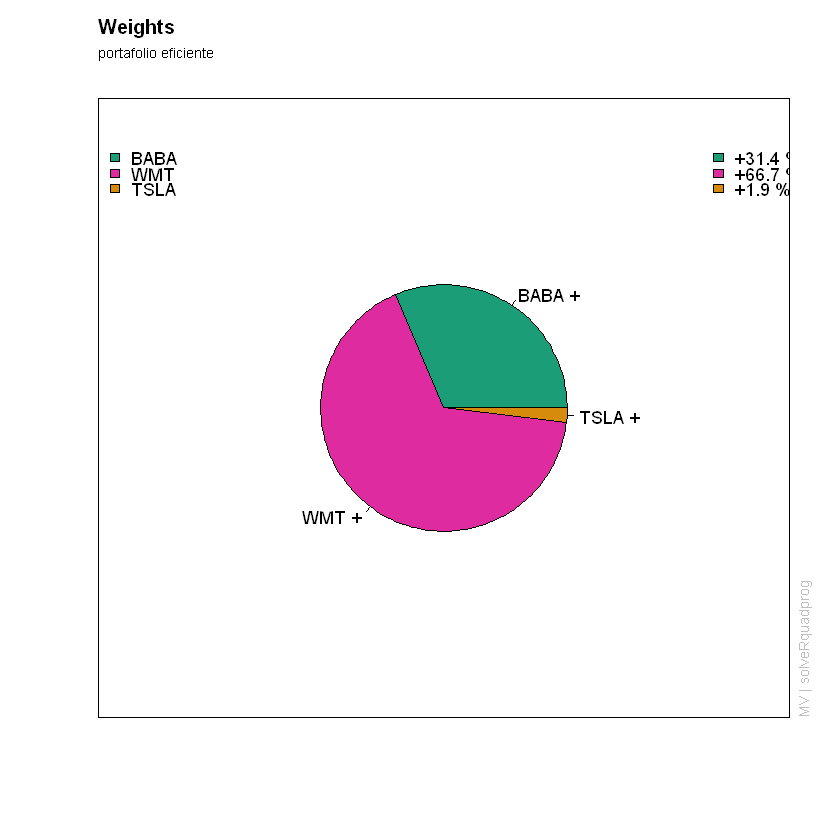
../../_images/output_9_03.png

De forma similar se contruye el gráfico circular para el portafolio tangente.

#torta portafolio tangente
win.graph(15,13)
weightsPie(Portafolio_tang, col= col, radius = 0.5)
mtext(text = "portafolio tangente", side = 3, line = 1.5, font = 1, cex = 0.7, adj = 0)
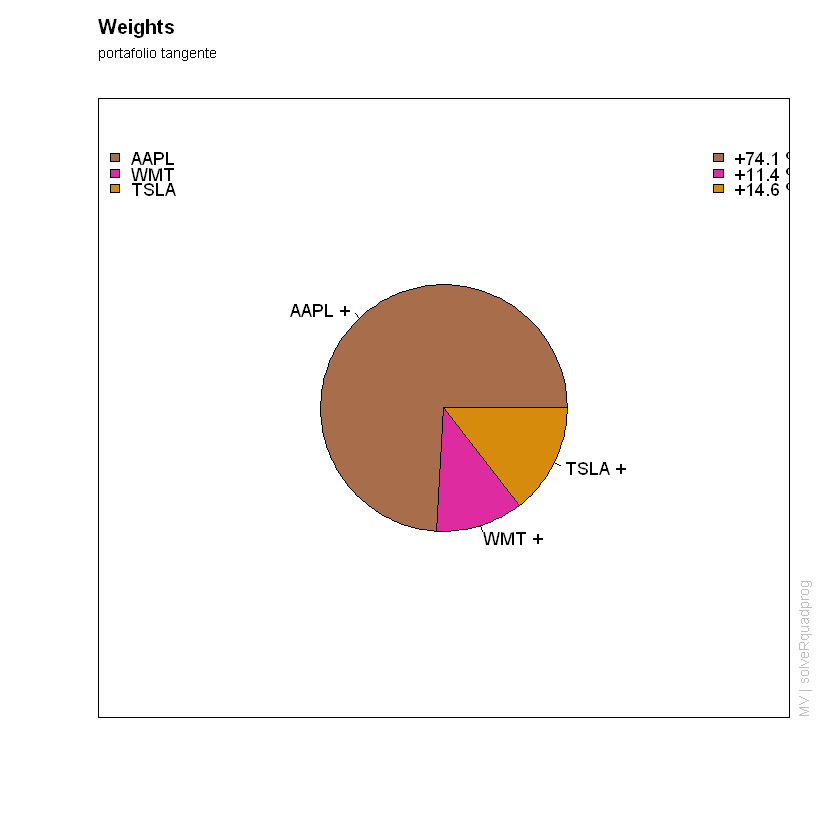
../../_images/output_11_03.png

Beta del portafolio

Obtención de los rendimientos del portafolio elegido

Por lo genral, el portafolio tangente es el portafolio que se elige como mejor premio para el inversionista. A este, se le debe realizar un análisis de sensibilidad para determinar, cuál es la cantidad de riesgo sistemático, este riesgo se determina por medio del cálculo del Beta, que se consigue contrastando mediante una regresión lineal simple, todos los rendiemientos diarios del portafolio tangente contra los rendimientos diarios del mercado. Esta regresión tiene el comportamiento de una línea recta por lo que la ecuación que la determinaes es la siguiente:

\[y= a+bx\]

\(b\) que acompaña la \(x\) es la pendiente, a su vez, puede ser tratada como el riesgo sistemático del portafolio contra el mercado. De esta forma, si \(\beta < 1\) se considera que el portafolio es menos sensible a los cambios en el mercado, por el contrario, si \(\beta > 1\), el portafolio tendrá mayor sensibilidad al mercado. el signo del coeficiente determinará la relación que existe entre el mercado y el portafolio, para \(\beta_1\) positivo se espera una relación directamente proporcional, y para \(\beta_1\) negativo, una relación inversamente proporcional.

Lo primero que se realiza es obetener los rendimientos diarios del portafolio tangente, para ello, se utiliza un ciclo for que recorra todas las filas [i] de la matríz de rendimientos nrow(Rdtos) y realice la suma producto con el vector de los pesos del portafolio tangente W_tang (objeto creado anteriormente)

#rendimientos del portafolio
rdto_port_tang= vector()
for(i in 1:nrow(Rdtos)){
  rdto_port_tang[i]= sum(Rdtos[i,]%*%W_tang)
}
head(rdto_port_tang,20)
  1. -0.00366527191926463
  2. 0.00126793777500628
  3. 0.00199084987075304
  4. 0.00363105533713878
  5. 0.000667874740728296
  6. -0.0103097984945859
  7. 0.0101384580243651
  8. 0.00687891201111615
  9. -0.000513275999864655
  10. 0.00965641448330918
  11. -0.00394629951575977
  12. -0.00538383463217754
  13. -0.0011157625438134
  14. -0.00535828297468948
  15. -0.00452481419886013
  16. -0.00937858103130249
  17. 0.00584692105102535
  18. 0.029692852222876
  19. 0.00431077449850838
  20. 0.0068800137317509

Para conocer el comportamiento del mercado, se deben obtener los datos de cotización del índice S&P 500. es importante aclarar que la elección del índice dependerá de las acciones con las que se encuentre trabajando, si se tienen acciones de USA, pueden utilizar SP500, DOW-JONES, NYSE o NASDAQ (si pertenecen a estas bolsas). Si son acciones colombianas, se deberá realizar con el COLCAP, o por ejemplo Alemania, con el índice DAX.

En este caso se obtienen los datos del SP500 y se crea el DF con los redimientos Rdto_mdo, tal como se explica en Obtención y Análisis de Rendimientos R

#Rdtos del mercado
getSymbols.yahoo(c('^GSPC'),env=globalenv(), from = "2019-02-12",to = Sys.Date())

SP500= GSPC$GSPC.Adjusted
Rdto_mdo=diff(log(SP500))
Rdto_mdo= Rdto_mdo[-1]
'^GSPC'

Una vez obtenidos los rendimientos del mercado y del portafolio, se porcede al ajuste de un modelo de regresión lineal, con la función lm(x~y), donde \(x\) representa la variable independiente, siendo los movimientos del mercado y \(y\) la dependiente que corresponde a los rendimientos del portafolio.

Con la función summary() se obitienen los coeficientes de la regresión \(\beta_0\) y \(\beta_1\), que corresponde al intercepto y la pendiente respectivamente. Para este caso se observan en la columna Estimate. Dado que el coficiente que interesa es el que acompaña a rdto_port_tang 0.7330308, se extrae el coeficiente con Beta=regresion$coefficients[2]. En este caso particular el portafolio es menos sesible a los cambios de mercado, es decir, por un cambio de un 1% en el rendimiento del mercado, el rendimiento del portafolio subirá un 0.73%.

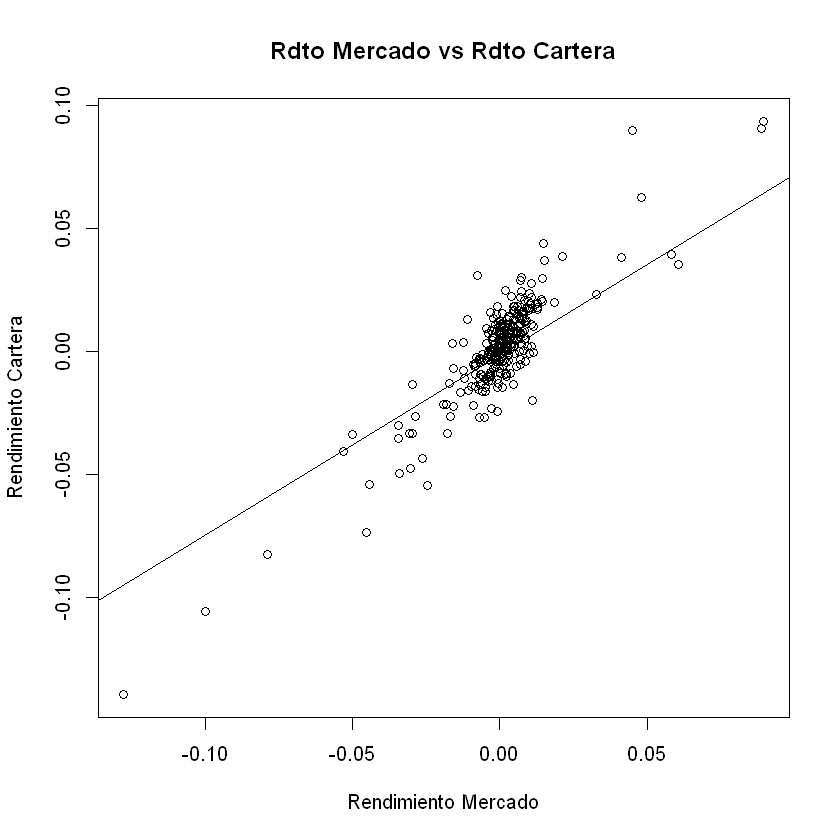
Para visualizar el gráfico de dispersión, se hace uso de la función plot(), contrastando el rendimiento del mercado Rdto_mdo contra el rendimiento del portafolio rdto_port_tang, ambos ingresados como vestores numéricos as.numeric(). Para la línea de la regresión se utiliza la función abline()

#Regresión para obtener el Beta del portafolio
regresion=lm(Rdto_mdo~rdto_port_tang)
summary(regresion)
Beta=regresion$coefficients[2]

#Gráfica Dispersión
plot(as.numeric(Rdto_mdo),as.numeric(rdto_port_tang), xlab='Rendimiento Mercado', ylab='Rendimiento Cartera', main="Rdto Mercado vs Rdto Cartera")
abline(regresion)

Call:
lm(formula = Rdto_mdo ~ rdto_port_tang)

Residuals:
      Min        1Q    Median        3Q       Max
-0.028985 -0.004045 -0.000233  0.004186  0.035841

Coefficients:
                 Estimate Std. Error t value Pr(>|t|)
(Intercept)    -0.0012409  0.0004893  -2.536   0.0118 *
rdto_port_tang  0.7330308  0.0222104  33.004   <2e-16 *
---
Signif. codes:  0 '*' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.008244 on 283 degrees of freedom
Multiple R-squared:  0.7938,        Adjusted R-squared:  0.793
F-statistic:  1089 on 1 and 283 DF,  p-value: < 2.2e-16
../../_images/output_17_13.png

Ratio de Treynor

Similar al ratio Sharpe, el ratio de Treynor, permite evaluar el premio que se le otorga al inversionista por asumir una porción del riesgo sistemático. De nuevo, entre mayor sea el Ratio de Treynor, mejor será el premio. El ratio de Treynor está determinado por la fórmula:

\[Treynor= \frac{(R_p)- R_f}{\beta}\]
## Ratio de Treynor
Treynor_tang=(Rport_tang[2]-rf)/Beta

Práctica 6:

Con las acciones tomadas para la práctica # 5, identifique cuáles son los ratios de desempeño y selección para el portafolio tangente y eficiente, es decir, calcule para ambos portafolios:

a. Los pesos exactos de los portafolios

b El ratio de Sharpe

c. El Betha del portafolio

d El ratio de Treynor.