Análisis de datos

Función

Significado

summary(data)

Resumen estadístico

min(data)

Mínimo

max(data)

Máximo

mean(data)

Media aritmética

median(data)

Mediana

range(data)

Rango

sd(data)

Desviación estándar

var(data)

Varianza

cov(data)

Covarianza

cor(data)

Coeficiente de correlación

quantile(data, 0.05)

Percentil del 5%

quantile(data, 0.80)

Percentil del 80%

skewness(data)

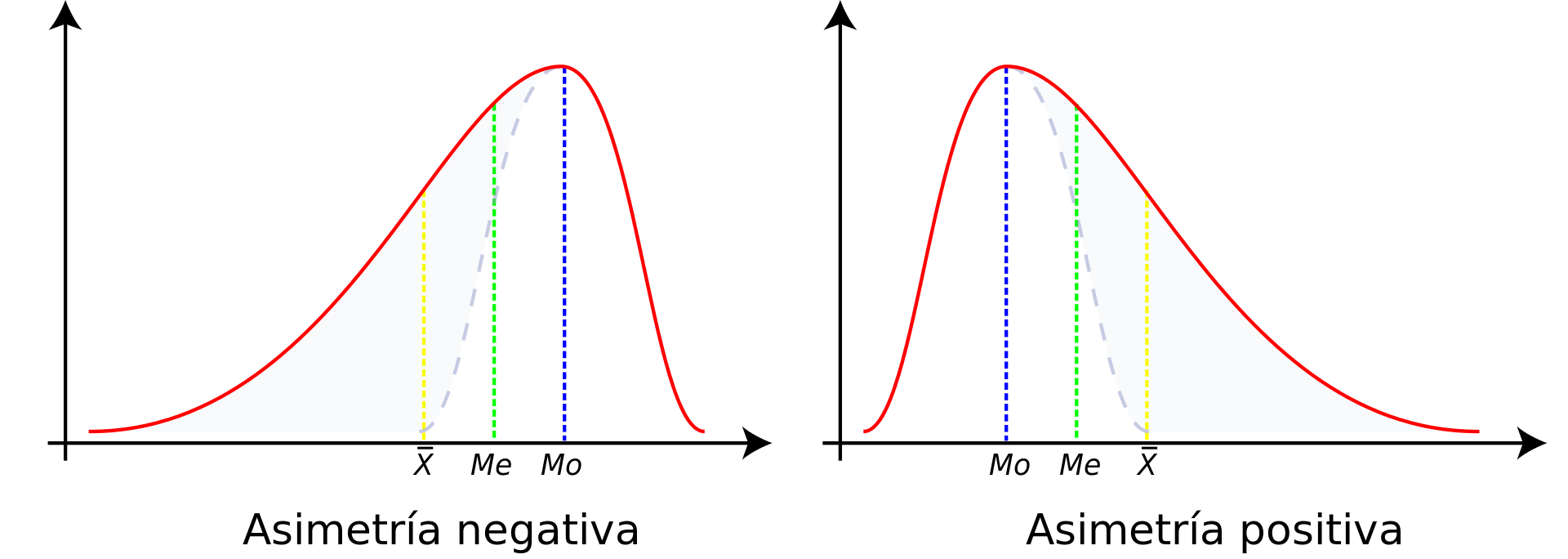
Asimetría

kurtosis(data)

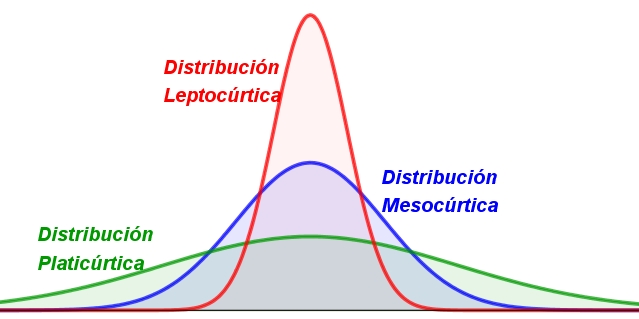
Curtosis

Cargar datos:

datos = read.csv("Datos.csv", sep = ";", dec = ",", header = T)
datos
A data.frame: 8 × 5
NombreEdadGéneroPesoEstrato
<fct><int><fct><dbl><int>
Ángela 22F 62.53
José 10M 75.84
Juan 15M 54.43
Manuela35F 73.63
Maribel50F 70.05
Antonio45M180.04
Alicia 1F 15.71
Luis 32M103.55

summary:

summary(datos$Peso)

 Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
15.70   60.48   71.80   79.44   82.72  180.00

La función basicStats()calcula más estadíticos que summary().

Primero se instala el siguiente paquete: install.packages("fBasics")

library(fBasics)

Loading required package: timeDate

Loading required package: timeSeries

print(basicStats(datos$Peso))

            X..datos.Peso
nobs             8.000000
NAs              0.000000
Minimum         15.700000
Maximum        180.000000
1. Quartile     60.475000
3. Quartile     82.725000
Mean            79.437500
Median          71.800000
Sum            635.500000
SE Mean         16.799457
LCL Mean        39.713096
UCL Mean       119.161904
Variance      2257.774107
Stdev           47.516041
Skewness         0.874260
Kurtosis        -0.067399

Medidas de tendencia central:

  • Media.

  • Mediana.

  • Moda.

# Media:

mean(datos$Peso)
79.4375
# Mediana:

median(datos$Peso)
71.8

La moda es el valor que más se repite, es decir, el de mayor frecuencia.

Con la función table() se calculan las frecuencias.

table(datos$Estrato)

1 3 4 5
1 3 2 2

El Estrato 3 es el de mayor frecuencia. Esta es la moda, entonces la moda es el máximo de las frecuencias.

moda <- max(table(datos$Estrato))
moda
3

Medidas de dispersión:

  • Rango.

  • Varianza.

  • Desviación estándar.

  • Coeficiente de variación.

# Rango:

range(datos$Peso)
  1. 15.7
  2. 180
# Varianza:

var(datos$Peso)
2257.77410714286
# Desviación estándar:

sd(datos$Peso)
47.5160405246782
# Desviación estándar:

sqrt(var(datos$Peso))
47.5160405246782
\[coeficienteVariación = \frac{DesviaciónEstándar}{Media}\]
# Coeficiente de variación:

coef_var <- sd(datos$Peso)/mean(datos$Peso)
coef_var
0.598156292993588

Medidas de posición:

Cuartiles:

Los diagramas de cajas y bigotes es una forma visual de analizar las medidas de posición.

# Cuartiles.

print(quantile(datos$Peso))

    0%     25%     50%     75%    100%
15.700  60.475  71.800  82.725 180.000

# Q1 - primer cuartil - percentil del 25%:

quantile(datos$Peso, 0.25)
25%: 60.475
# Q2 - segundo cuartil - percentil del 50%:

quantile(datos$Peso, 0.50)   # Este es el valor de la mediana.
50%: 71.8
# Q3 - tercer cuartil - percentil del 75%:

quantile(datos$Peso, 0.75)
75%: 82.725

Rango intercuatil (RIC):

\[RIC = Q_3 - Q_1\]
RIC = quantile(datos$Peso, 0.75) - quantile(datos$Peso, 0.25)
RIC  # Rango de un 50%
75%: 22.25
RIC = as.numeric(RIC) # para quitarle la etiqueta de 75%
RIC
22.25

Medidas de forma:

  • Sesgo (asimetría): skewness.

  • Curtosis: kurtosis.

Asimetría

Asimetría

Curtosis

Curtosis

# Asimetría:

skewness(datos$Peso) # Resultados: sesgo positivo.
0.874260494208836
# Curtosis:

kurtosis(datos$Peso) # Resultado: platicúrtica.
-0.0673990420899138