Introducción al análisis multivariado

Con el análisis multivariado o multivariante de datos se busca:

1. Describir

2. Resumir

3. Agrupar

4. Clasificar

5. Relacionar

Datos univariantes:

Una sola variable aleatoria con $n$ observaciones.

Datos multivariantes:

$p > 1$ variables aleatorias con $n$ observaciones.

Representación matricial de datos multivariantes:

Las variables se ubican en las columnas y las filas son las observaciones. El total de filas, $n$, es el tamaño de la muestra, $n$ elementos muestrales.

$ :raw-latex:`left`(

:raw-latex:`\right`) $

Representación vectorial de datos multivariantes:

La anterior matriz se puede representar de forma vectorial en función de las columnas así:

\[X = [X_1, X_2, X_3, ..., X_p]\]

Donde $X_j \in \mathbb R^n, \forall j = 1,2,3,...,p$

Las $p$ variables aleatorias forman una variable aleatoria multivariante $X$.

Tipos de variables:

1. Cuantitativas: datos numéricos.

Continuas: valores reales dentro de un intervalo. Ejemplo, precio de las acciones.
Discretas: valores numerables o contables. Ejemplo, estrato.

2. Cualitativas: atributos o categorías.

En el análisis exploratorio de datos multivariados se visualiza las variables cuantitativas y las variables cualitativas aportan información adicional como clasificar los datos por atributos o categorías.

Análisis exploratorio de datos multivariados:

Boxplot: se realiza para una variable y tiene algunos estadísticos como mediana y cuartiles. Son útiles para analizar la localización de la variable, desviación, asimetría y datos atípicos.
Histograma: se realiza para una variable y es una representación gráfica de las frecuencias. Permiten identificar la distribución de la variable, asimetría, localización, dispersión y datos atípicos.
Densidad Kernel: es la función de densidad de la variable que se dibuja encima del histograma, la función se llama Kernel. Tiene el mismo análisis que los histogramas. Se puede hacer para una variable o dos variables separando los datos por grupos (variable categórica). La función más usada es la Gaussiana.
Dispersión (scatterplot): para análisis entre dos variables. Se usan visualizar la distribución bivariada, determinar la relación entre pares de variables. También se puede hacer en 3D con una tercera variable.
Matriz de correlaciones: es una tabla numérica donde muestra el coeficiente de correlación entre pares de variables. Se mide el grado de relación lineal entre un par de variables aleatorias.
Radar: para tres o más variables cuantitativas. Los ejes están ubicados radialmente. Tiene otros nombres como gráfico de araña (spider), de estrellas o polar. Permiten observar las diferencias entre las magnitudes de cada variable.

Medidas descriptivas:

Para analizar cada variable por separado se puede calcular las siguientes medidas estadísticas.

Media.
Varianza.
Desviación estándar.

Para el análisis de la relación entre variables calculamos:

Covarianzas: matriz de varianzas-covarianzas.
Coeficientes de correlación: matriz de correlaciones.

datos = read.csv("EAM_2019.csv", sep = ";", dec = ",", header = T)
print(head(datos))

  ï..ciiu personal_mujer personal_hombre gasto_personal gasto_financiero
  1051             36             140        9352991          3240559
  1030             40             176        7334998          1468298
  3290             15             172        6668544          1547666
  3091             88             373       22088759         35203208
  3290             18              53        5219070          2861773
  3290             18              53        5219070          2861773
  costos_gastos_produccion gastos_adm_ventas inversion_AF    ventas
                6846304          22920307      4979745 192609248
                5941761          12310286      5615593 115741258
                6996020           2564695       773444  44580029
                4175751         171278876     10501572 162509864
               11037978          13691919      6423171  87324374
               11037978          13691919      6423171  87324374

colnames(datos)[1] = "ciiu"
names(datos)

'ciiu'
'personal_mujer'
'personal_hombre'
'gasto_personal'
'gasto_financiero'
'costos_gastos_produccion'
'gastos_adm_ventas'
'inversion_AF'
'ventas'

datos[,1] = as.character(datos[,1])
str(datos)

'data.frame':       420 obs. of  9 variables:
 $ ciiu                    : chr  "1051" "1030" "3290" "3091" ...
 $ personal_mujer          : int  36 40 15 88 18 18 43 23 108 197 ...
 $ personal_hombre         : int  140 176 172 373 53 53 215 97 149 70 ...
 $ gasto_personal          : int  9352991 7334998 6668544 22088759 5219070 5219070 9386665 4756263 11081213 8575341 ...
 $ gasto_financiero        : int  3240559 1468298 1547666 35203208 2861773 2861773 647945 630568 20390274 542136 ...
 $ costos_gastos_produccion: int  6846304 5941761 6996020 4175751 11037978 11037978 5445839 1622747 1843527 4002790 ...
 $ gastos_adm_ventas       : num  2.29e+07 1.23e+07 2.56e+06 1.71e+08 1.37e+07 ...
 $ inversion_AF            : int  4979745 5615593 773444 10501572 6423171 6423171 364272 265025 50853587 312822 ...
 $ ventas                  : num  1.93e+08 1.16e+08 4.46e+07 1.63e+08 8.73e+07 ...

Código en R:

library(ggplot2)

Boxplot:

Se crea el Boxplot para cada variable cuantitativa.

La primera columna de los datos no es cuantitativa, es una variable cualitativa con los códigos CIIU de la DIAN.

names(datos)

'ciiu'
'personal_mujer'
'personal_hombre'
'gasto_personal'
'gasto_financiero'
'costos_gastos_produccion'
'gastos_adm_ventas'
'inversion_AF'
'ventas'

Las nueve variables se graficarán dentro de un ciclo for empezando en 2 porque la primera columna tiene la variable categórica de la DIAN.

Para ingresar los nombres de las variables de forma automática se usa la función paste(), con la cual podemos indicar una función y arrojará el resultado como una etiqueta.

Con los Boxplot podemos identificar los datos atípicos por cada variable y asimetrías.

for(i in 2:9){
    print(ggplot(data = datos) +
                geom_boxplot(aes(x = datos[, i])) +
                coord_flip() +
                labs(title = "Encuesta nacional manufacturera",
                    subtitle = paste(names(datos)[i]),
                    x = "Frecuencia absoluta"))
}

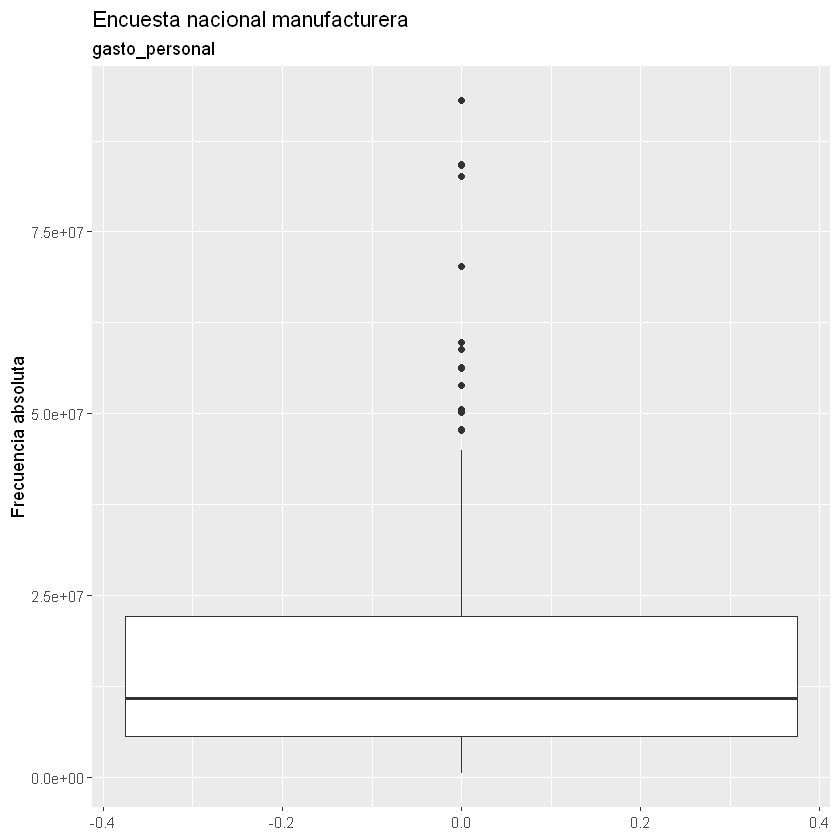
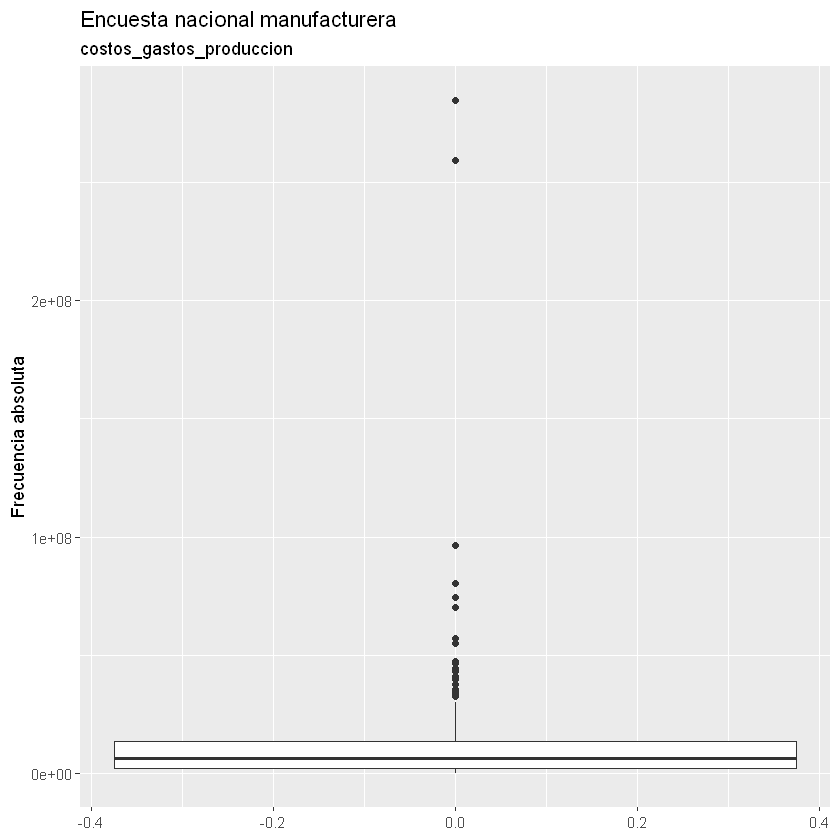
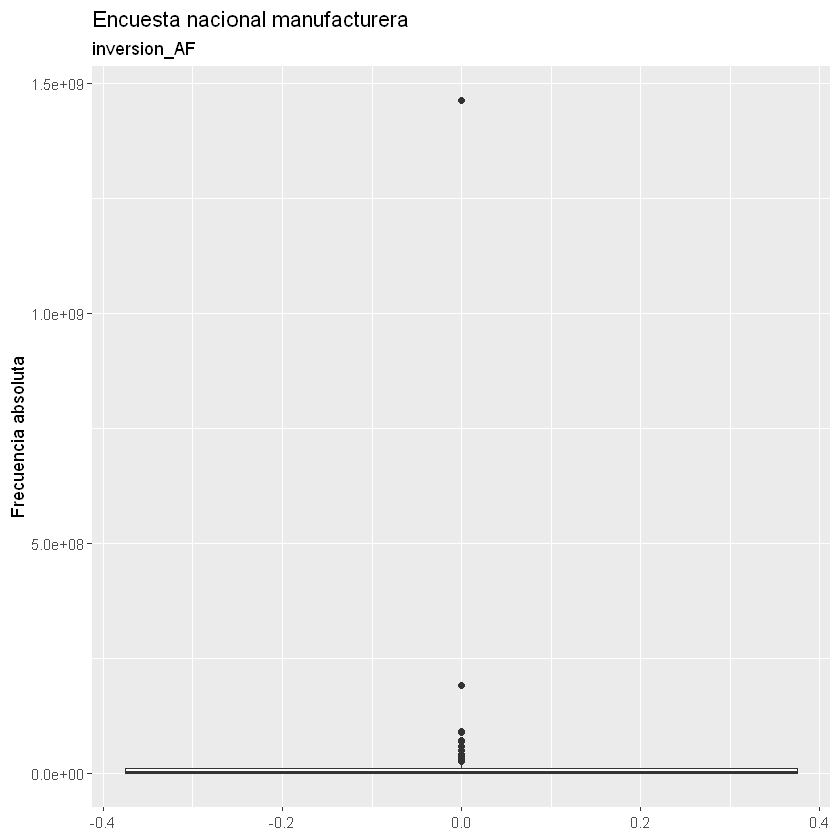
Histograma con kernel:

Función de densidad Kernel:

\[\hat{f_h} (x) = \frac{1}{nh} \sum {K \frac{x-x_i}{h}}\]

Donde $K$ es la función Kernel.

Para el Kernel Gaussiano $K$ es:

\[K(u) = \frac{1}{2 \pi}exp^{-\frac{u^2}{2}}\]

$h$ es el ancho de banda. Entre más pequeño es $h$, mayor es el sobre ajuste y la curve es menos suavizada. En ggplot2 la densidad Kernel se hace con stat_density(kernel = "gaussian"). Para cambiar $h$ se agrega el argumento adjust =, por defecto es adjust = 1.

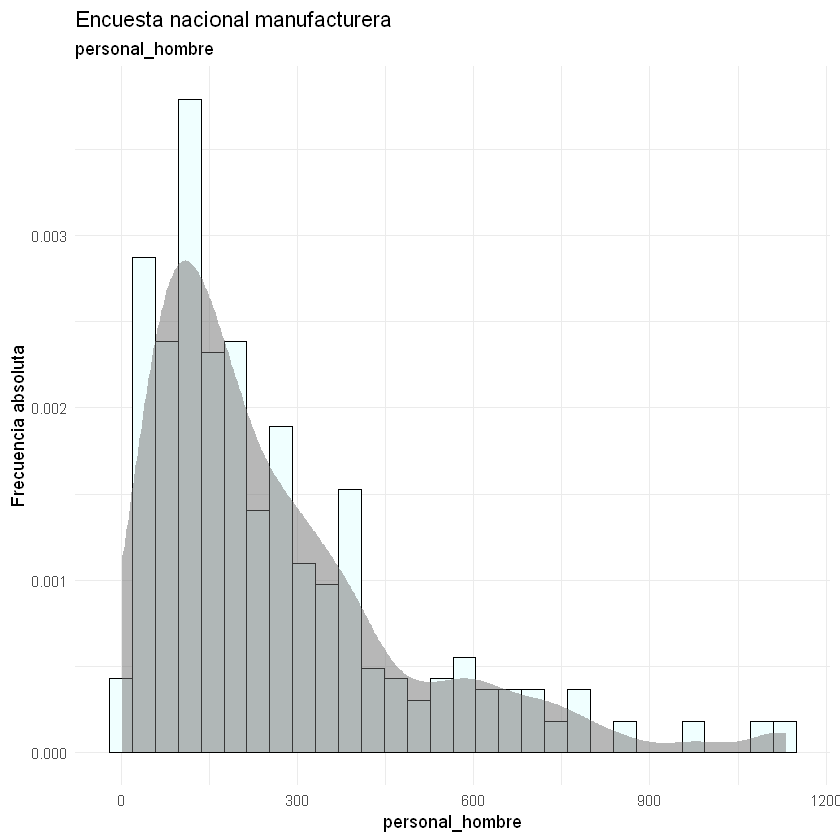
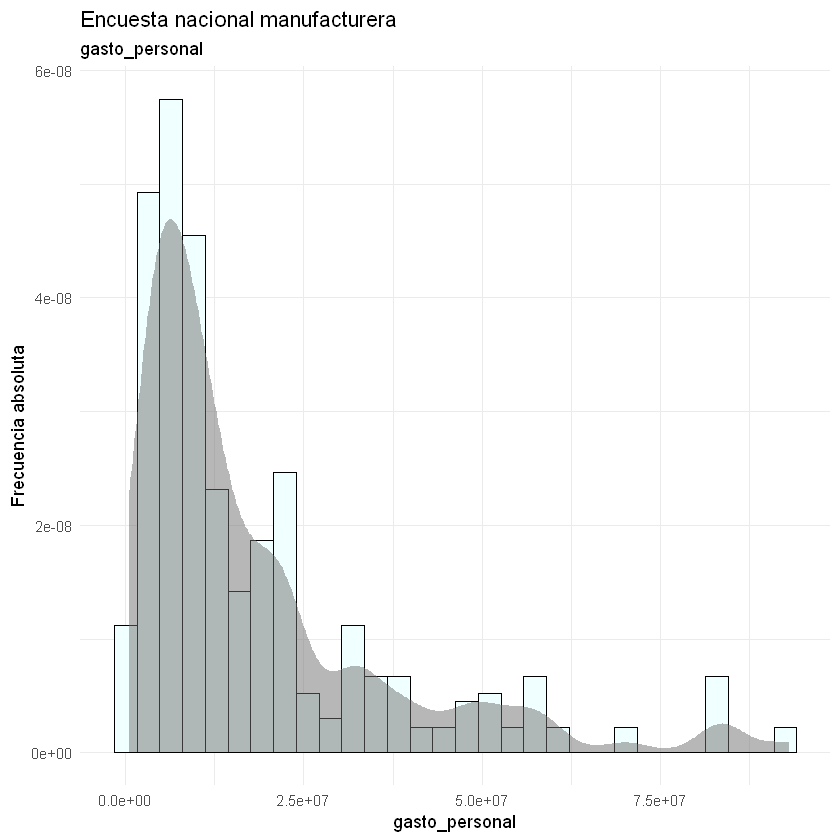
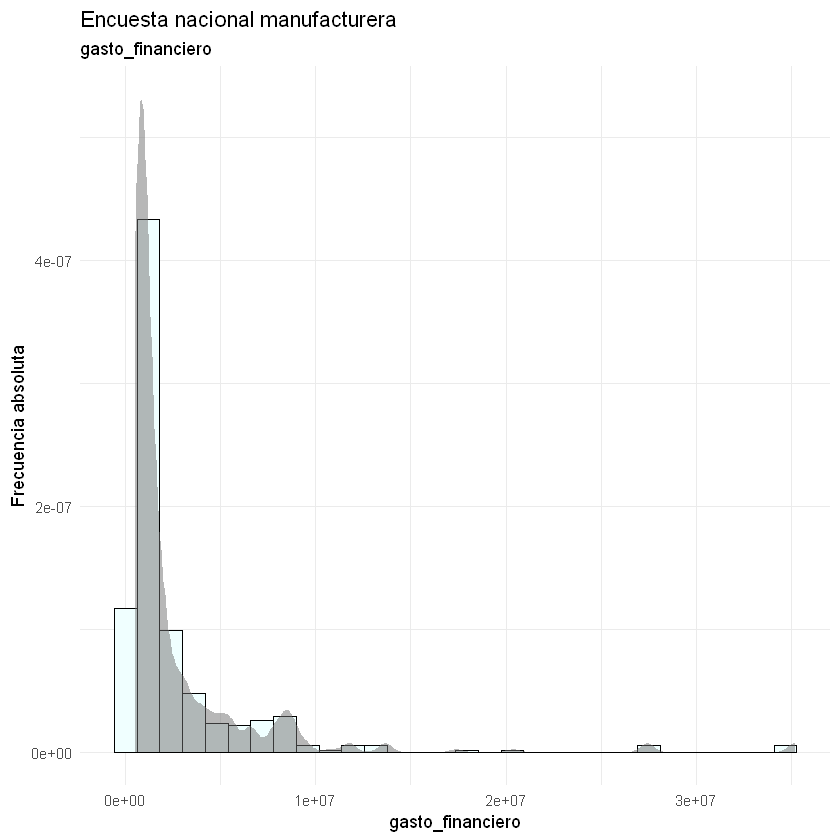
Las asimetrías se observan más fácilmente en los histogramas. También, podemos identificar si los datos atípicos tienen alta o baja frecuencia.

for(i in 2:9){
    print(ggplot(data = datos) + aes(x = datos[, i]) +
                geom_histogram(aes(y = ..density..),
                               bins = 30,
                               fill = "#F0FFFF", color = "black") +
                stat_density(kernel = "gaussian", fill = "#707070", alpha = 0.5) +
                theme_minimal() +
                labs(title = "Encuesta nacional manufacturera",
                    subtitle = paste(names(datos)[i]),
                    y = "Frecuencia absoluta",
                    x = paste(names(datos)[i])))
}

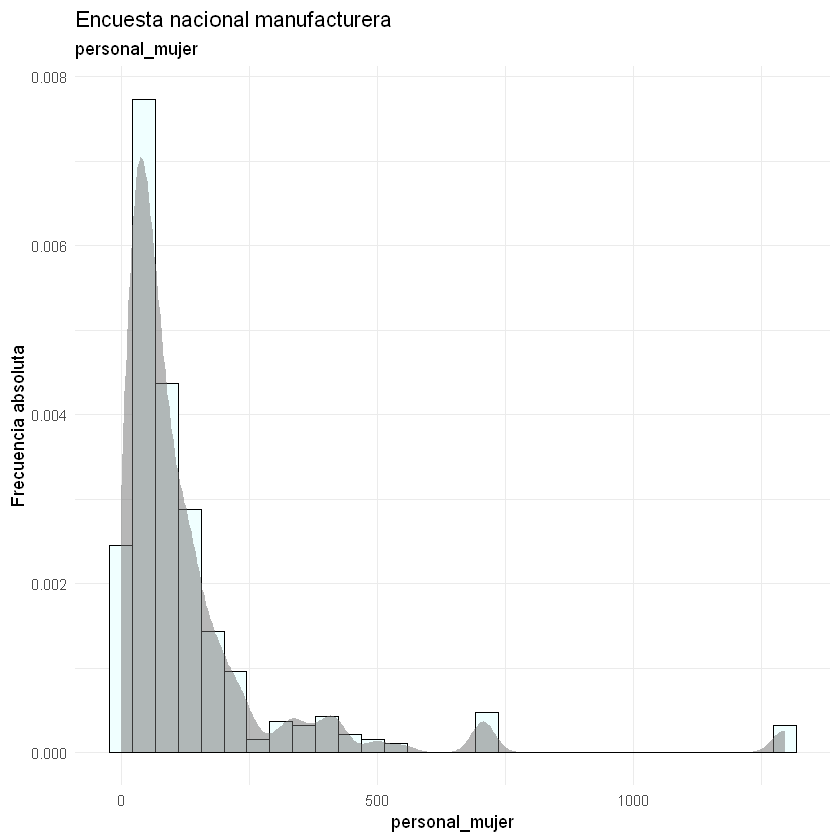
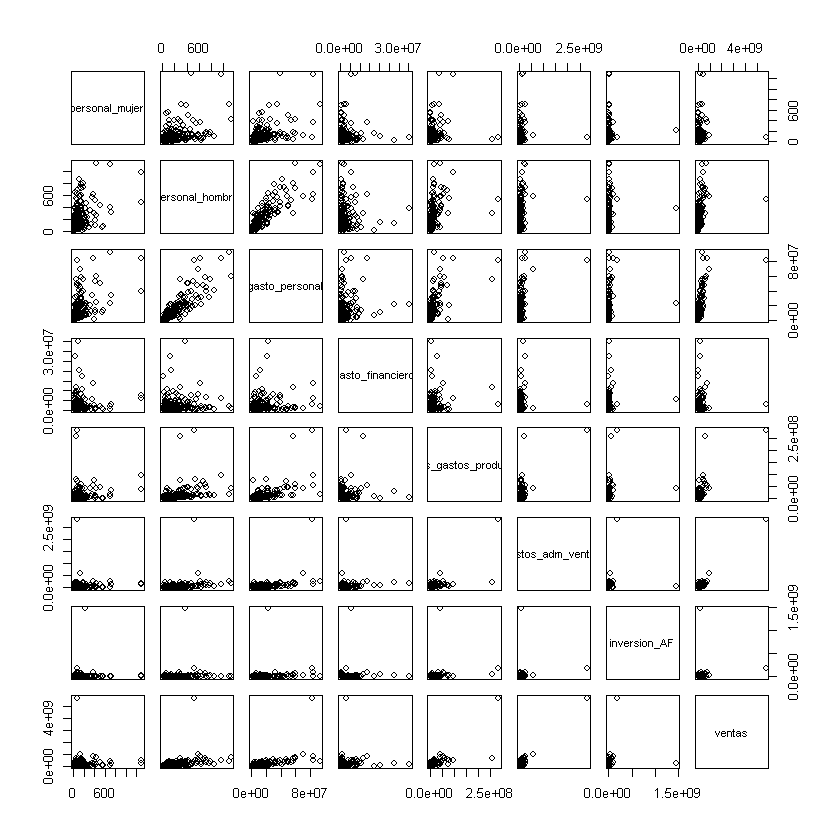
Matríz de dispersión:

La base de R tiene la función pairs() para construir matrices de dispersión.

Recuerde que las variables cuantitativas están desde la columna 2 hasta la 9.

pairs(datos[, 2:9])

El paquete GGally es una extensión de ggplot2 y se usa para crear la matríz de dispersión con la función ggpairs().

GGally funciona en versiones superiores de 3.1 en R y versiones superiores de 3.3.4 en ggplot2.

packageVersion("ggplot2")

R.version

Después, instalar el paquete así: install.packages("GGally")

library(GGally)

Registered S3 method overwritten by 'GGally':
  method from
  +.gg   ggplot2

ggpairs(datos[,2:9])

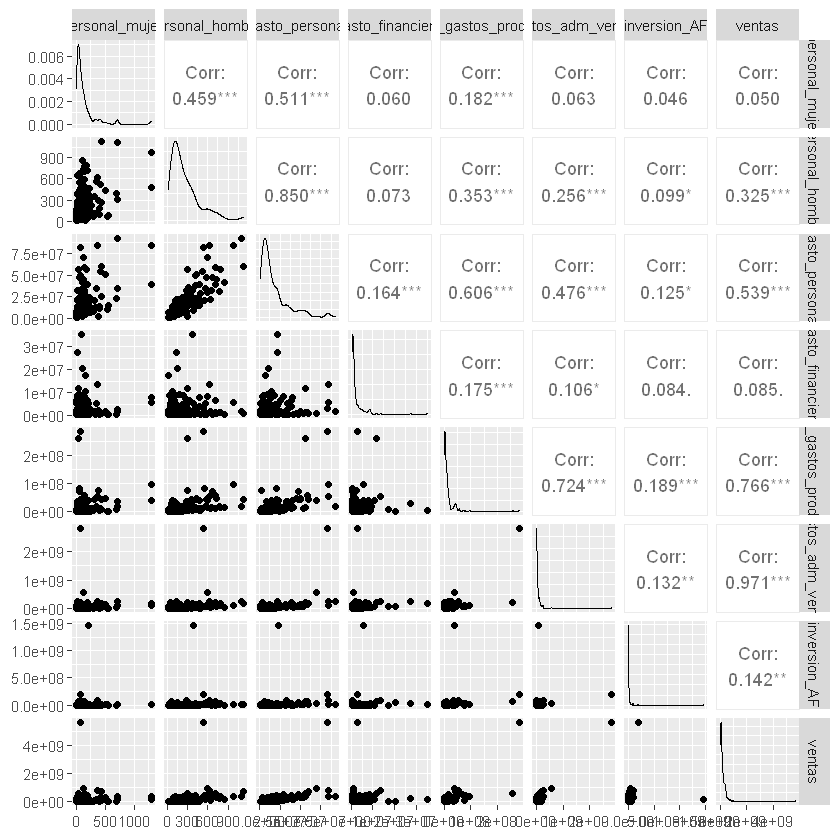
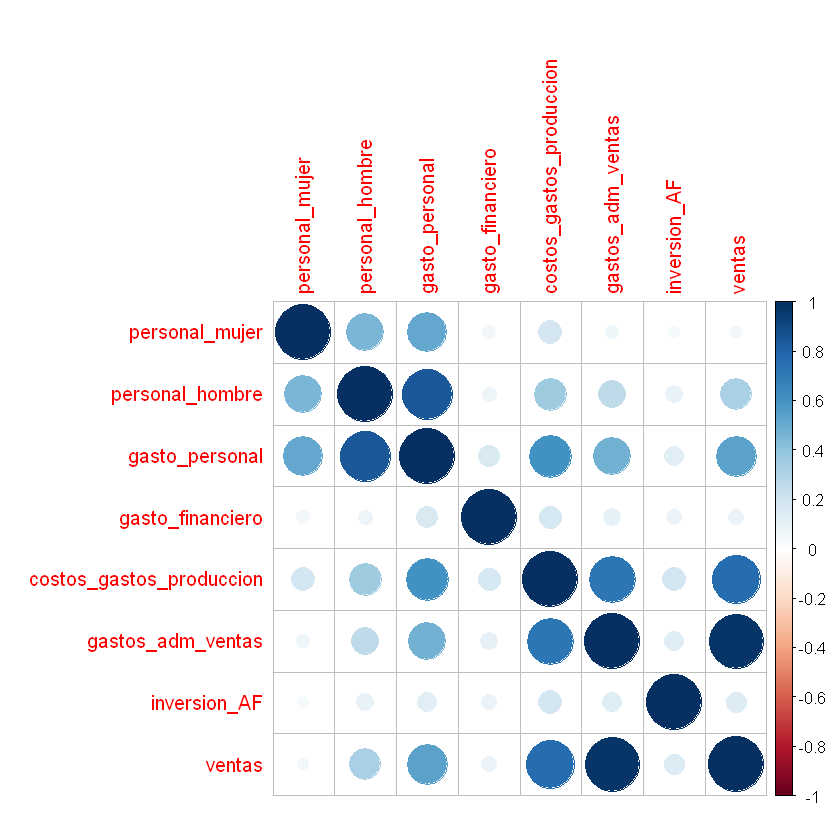
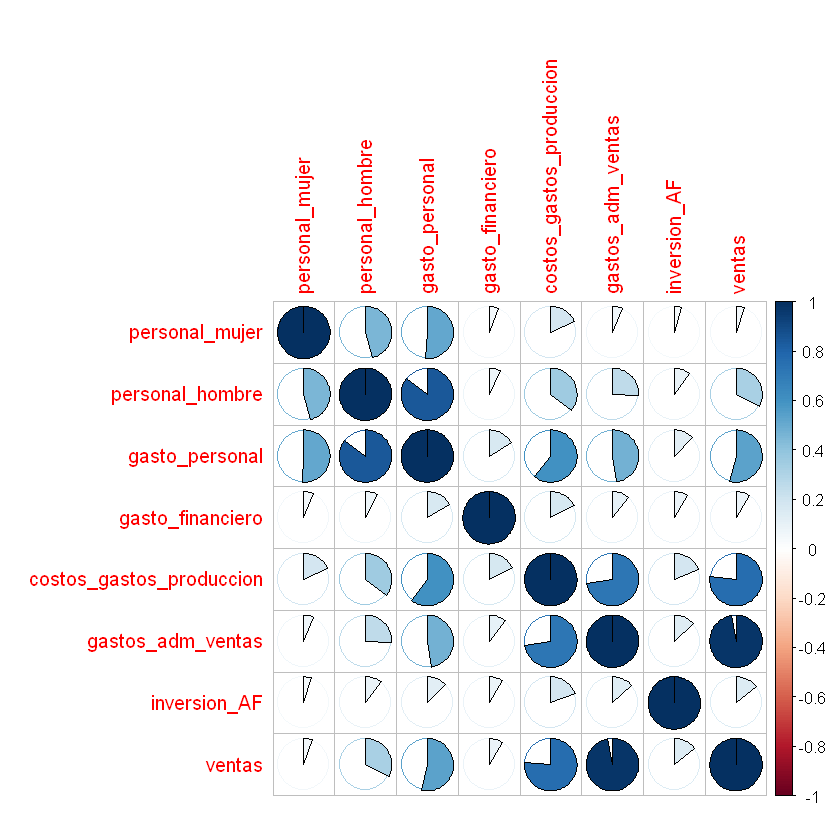
Matríz de correlaciones:

La base de R tiene la función cor() para construir la matríz de correlación

cor(datos[,2:9])

A matrix: 8 × 8 of type dbl
	personal_mujer	personal_hombre	gasto_personal	gasto_financiero	costos_gastos_produccion	gastos_adm_ventas	inversion_AF	ventas
personal_mujer	1.00000000	0.45918261	0.5114733	0.05951392	0.1815275	0.0625563	0.04607581	0.05007149
personal_hombre	0.45918261	1.00000000	0.8495829	0.07267965	0.3534615	0.2558384	0.09931522	0.32545296
gasto_personal	0.51147327	0.84958291	1.0000000	0.16354049	0.6056747	0.4755711	0.12504179	0.53904261
gasto_financiero	0.05951392	0.07267965	0.1635405	1.00000000	0.1753652	0.1062969	0.08373504	0.08489441
costos_gastos_produccion	0.18152747	0.35346147	0.6056747	0.17536517	1.0000000	0.7237423	0.18938634	0.76599555
gastos_adm_ventas	0.06255630	0.25583836	0.4755711	0.10629691	0.7237423	1.0000000	0.13218655	0.97091339
inversion_AF	0.04607581	0.09931522	0.1250418	0.08373504	0.1893863	0.1321865	1.00000000	0.14171846
ventas	0.05007149	0.32545296	0.5390426	0.08489441	0.7659955	0.9709134	0.14171846	1.00000000

Con el paquete GGally se puede crear una matríz de correlaciones aplicando la función ggcorr()

ggcorr(datos[,2:9])

Usted puede buscar muchas formas para representar la matríz de correlaciones. Veamos el siguiente ejemplo:

Función corrplot() de la librería con el mismo nombre.

install.packages("corrplot")

library("corrplot")

corrplot 0.92 loaded

Primero se crea la matríz de correlaciones con la función de la base de R llamada cor().

correlaciones <- cor(datos[,2:9])

corrplot(correlaciones, method="circle")

corrplot(correlaciones, method="pie")

corrplot(correlaciones, method="color")

corrplot(correlaciones, method="number")